Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение прототипов В 4 8-9 класс
Содержание
- 1. Решение прототипов В 4 8-9 класс
- 2. № 27949Найдите радиус R окружности, описанной около
- 3. № 27950Найдите радиус окружности, описанной около правильного
- 4. № 27951Найдите радиус окружности, вписанной в треугольник
- 5. № 27952Найдите радиус r окружности, вписанной в
- 6. № 77152Основания равнобедренной трапеции равны 6 и
- 7. № 27944Около окружности, радиус которой равен
- 8. № 27945Около окружности, радиус которой равен
- 9. № 27946Найдите радиус окружности, описанной около прямоугольного
- 10. № 27947Найдите радиус окружности, описанной около прямоугольника
- 11. № 27939В четырехугольник ABCD вписана окружность, AB=10,
- 12. № 27940Периметр четырехугольника, описанного около окружности, равен
- 13. № 27942Три стороны описанного около окружности четырехугольника
- 14. № 27934Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.РешениеОтвет: 1,5
- 15. № 27935Окружность, вписанная в равнобедренный треугольник, делит
- 16. № 27936Боковые стороны трапеции, описанной около окружности,
- 17. № 27937Около окружности описана трапеция, периметр которой
- 18. № 27938Периметр прямоугольной трапеции, описанной около окружности,
- 19. № 27929Периметр правильного шестиугольника равен 72. Найдите
- 20. № 27930Угол между стороной правильного n-угольника, вписанного
- 21. № 27925Боковая сторона равнобедренной трапеции равна ее
- 22. Слайд 22
- 23. Скачать презентанцию
№ 27949Найдите радиус R окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите .Решение.Так как окружность описана около прямоугольного треугольника, то ее центр лежит на
Слайды и текст этой презентации
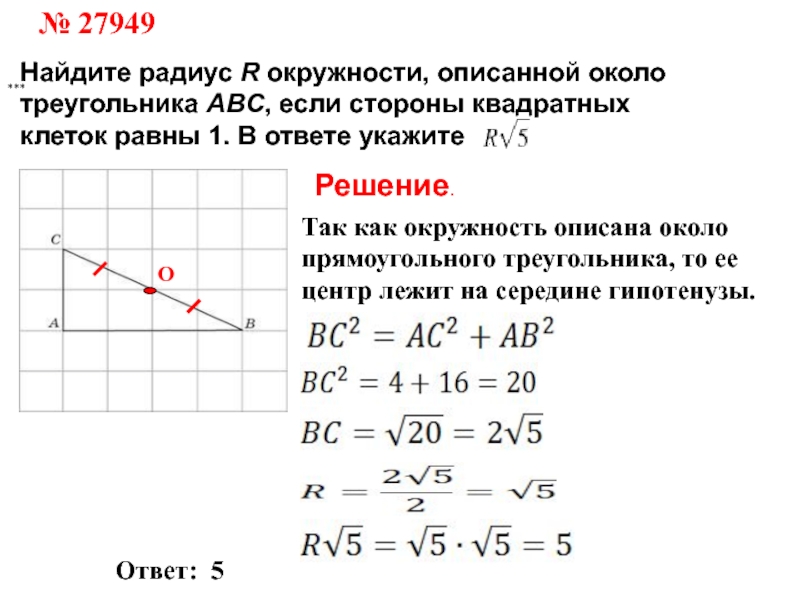
Слайд 2№ 27949
Найдите радиус R окружности, описанной около треугольника ABC, если
стороны квадратных клеток равны 1. В ответе укажите .
Решение.
Так
как окружность описана около прямоугольного треугольника, то ее центр лежит на середине гипотенузы.
***
Ответ: 5
О
Слайд 3№ 27950
Найдите радиус окружности, описанной около правильного треугольника ABC, считая
стороны квадратных клеток равными 1.
Решение
Так как треугольник правильный, то центр
окружности описанной около него лежит на медиане, которая является биссектрисой и высотой.BD=3.
D
Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то ВО=2, OD=1, значит R=2.
Ответ: 2
О
Слайд 4№ 27951
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны
квадратных клеток равными 1.
Решение.
Центр окружности, вписанной в треугольник лежит на
пересечении биссектрис. О
D
F
N
OD=OF=ON=r
(по гипотенузе и острому углу), FODC -квадрат
Пусть FC=CD=x, тогда AF=3-x, значит AN=3-x,
AB=5, тогда NB=5-AN=5-3+x=2+x, BD=4-CD=4-x.
Так как NB=BD, то 2+x=4-x, откуда x=1, значит FC=1, r=1.
Ответ: 1
Слайд 5№ 27952
Найдите радиус r окружности, вписанной в четырехугольник ABCD. В
ответе укажите
Решение
Полученные прямоугольные треугольники равны, значит
BC=CD=AD=AB=
ABCD – квадрат,
так как окружность вписана в него, то сторона квадрата через радиус вписанной окружности вычисляется по формуле:Ответ: 5
Слайд 6№ 77152
Основания равнобедренной трапеции равны 6 и 12. Синус острого
угла трапеции равен 0,8. Найдите боковую сторону.
А
В
С
D
12
6
Решение. sinD=0,8, значит cosD=0,6
Так как трапеция равнобедренная, то углы при основании равны, AE=BF как высоты, треугольники равны, значит DE=3, CF=3, EF=6.
E
F
Ответ: 5
Слайд 7№ 27944
Около окружности, радиус которой равен ,
описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
Решение
Центр вписанной
и описанной окружностей около квадрата совпадают.Сторона правильного четырехугольника через радиус вписанной окружности выражается формулой:
Через радиус описанной окружности выражается формулой:
О
Ищем сторону квадрата:
Тогда
Ответ: 4
Слайд 8№ 27945
Около окружности, радиус которой равен , описан
правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
Решение.
О
Сторона правильного
шестиугольника черезрадиус вписанной окружности выражается
формулой:
Через радиус описанной окружности выражается формулой:
Найдем сторону шестиугольника:
Значит R=1.
Ответ: 1
Слайд 9№ 27946
Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если
стороны квадратных клеток равны 1.
Решение.
Так как центр окружности, описанной около
прямоугольного треугольника лежит на середине гипотенузы, а по рисунку АВ=5, то
R=2,5
Ответ: 2,5
Слайд 10№ 27947
Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны
квадратных клеток равны 1.
Решение.
Из прямоугольных треугольников ВС=
AD=
Так как
окружность описана околопрямоугольника, то ее центр совпадает с точкой пересечения диагоналей, а диагональ BD=5, значит радиус равен 2,5.
Ответ: 2,5.
О
Напоминание:
У прямоугольника
диагонали равны.
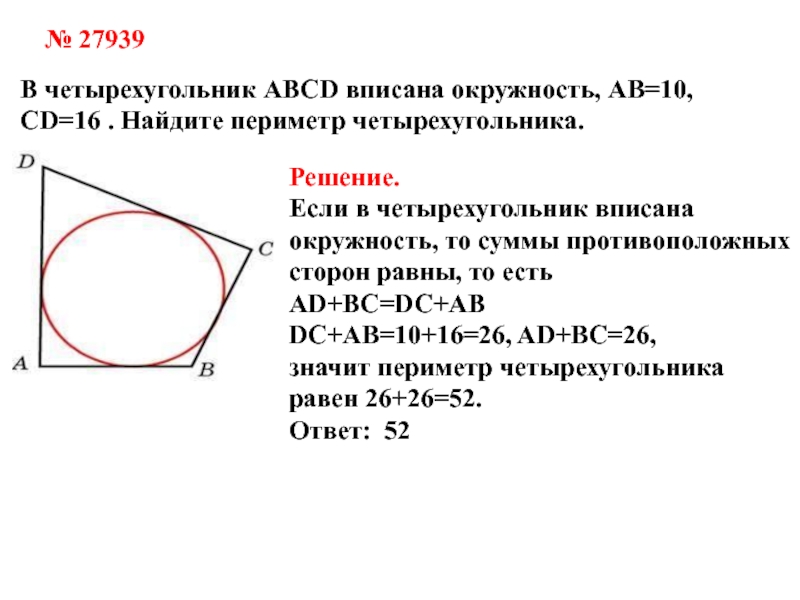
Слайд 11№ 27939
В четырехугольник ABCD вписана окружность, AB=10, CD=16 . Найдите
периметр четырехугольника.
Решение.
Если в четырехугольник вписана окружность, то суммы противоположных
сторон равны,
то есть AD+BC=DC+AB
DC+AB=10+16=26, AD+BC=26,
значит периметр четырехугольника
равен 26+26=52.
Ответ: 52
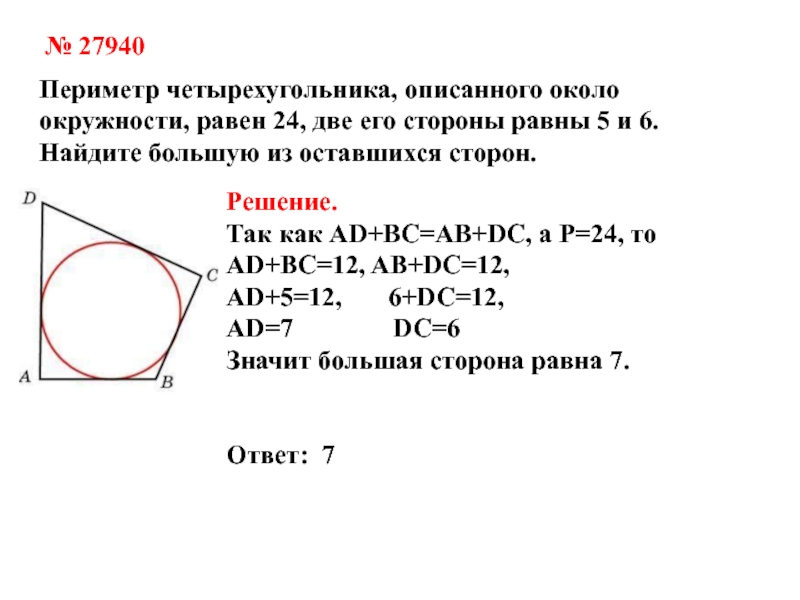
Слайд 12№ 27940
Периметр четырехугольника, описанного около окружности, равен 24, две его
стороны равны 5 и 6. Найдите большую из оставшихся сторон.
Решение.
Так
как AD+BC=AB+DC, а P=24, то AD+BC=12, AB+DC=12,
AD+5=12, 6+DC=12,
AD=7 DC=6
Значит большая сторона равна 7.
Ответ: 7
Слайд 13№ 27942
Три стороны описанного около окружности четырехугольника относятся (в последовательном
порядке) как Найдите
большую сторону этого четырехугольника, если известно, что его периметр равен 32.Решение
AB+DC=AD+BC=16
Пусть AB=x, AD=2x, BC=3x,
x+DC=16, 2x+3x=16, x=3,2,
DC=16-3,2=12,8
Ответ: 12,8
Слайд 14№ 27934
Боковые стороны равнобедренного треугольника равны 5, основание равно 6.
Найдите радиус вписанной окружности.
Решение
Ответ: 1,5
Слайд 15№ 27935
Окружность, вписанная в равнобедренный треугольник, делит в точке касания
одну из боковых сторон на два отрезка, длины которых равны
5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.D
5
3
Решение.
Центр вписанной окружности лежит на пересечении биссектрис, СК, проведенная к основанию является высотой и медианой. Выделенные треугольники равны по гипотенузе и острому углу, значит DB=КВ=3, то есть АВ=6.
Р(АВС)=8+8+6=22
Ответ: 22
К
3
r
r
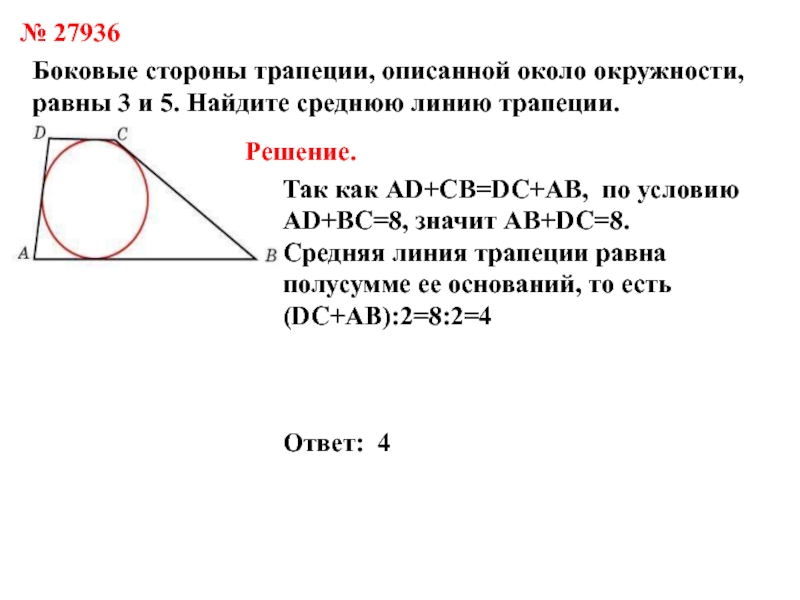
Слайд 16№ 27936
Боковые стороны трапеции, описанной около окружности, равны 3 и
5. Найдите среднюю линию трапеции.
Решение.
Так как AD+CB=DC+AB, по условию
AD+BC=8, значит
AB+DC=8.Средняя линия трапеции равна полусумме ее оснований, то есть
(DC+AB):2=8:2=4
Ответ: 4
Слайд 17№ 27937
Около окружности описана трапеция, периметр которой равен 40. Найдите
ее среднюю линию.
Решение
Так как AD+CB=AB+DC=20, то средняя линия равна:
(AB+DC):2=20:2=10Ответ: 10
Слайд 18№ 27938
Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее
большая боковая сторона равна 7. Найдите радиус окружности.
Решение.
Так как
AD+BC=AB+DC=11, то AD+7=11, AD=11-7=4.Радиус окружности равен: AD:2=4:2=2
Ответ: 2
.
r
r
O
Слайд 19№ 27929
Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
Решение.
Так как шестиугольник правильный, то найдем его сторону: АВ=72:6=12.
Сторона правильного
шестиугольника выражается через радиус описанной окружности формулой АВ=R, значит R=12, а диаметр равен 24.Ответ: 24
Слайд 20№ 27930
Угол между стороной правильного n-угольника, вписанного в окружность, и
радиусом этой окружности, проведенным в одну из вершин стороны, равен
Найдите n.•
О
54
54
R
R
R
Решение
Треугольники равнобедренные, значит углы при основании равны, значит внутренний угол n-угольника равен
Сумма внутренних углов выпуклого n-угольника равна:
где n- число сторон.
Тогда сумма внутренних углов данного n-угольника равна 108n, составим уравнение: 108n=
108n-180n=-360
72n= - 360
n=5
Ответ: 5
Слайд 21№ 27925
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол
при основании равен , большее основание равно 12. Найдите
радиус описанной окружности этой трапеции.
Решение.
Так как трапеция равнобедренная, то углы при основании равны, угол D равен углу С и равны 120 градусов. Треугольник ADC равнобедренный, значит углы при основании по 30 градусов. Угол АСВ равен 90 градусов, треугольник АСВ прямоугольный и около него описана окружность, значит ее центр лежит на середине гипотенузы АВ, а так как АВ=12, значит радиус описанной окружности равен 6.
Ответ: 6
