Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение систем, содержащих показательные уравнения 11 класс
Содержание
- 1. Решение систем, содержащих показательные уравнения 11 класс
- 2. Проверка домашнего задания.
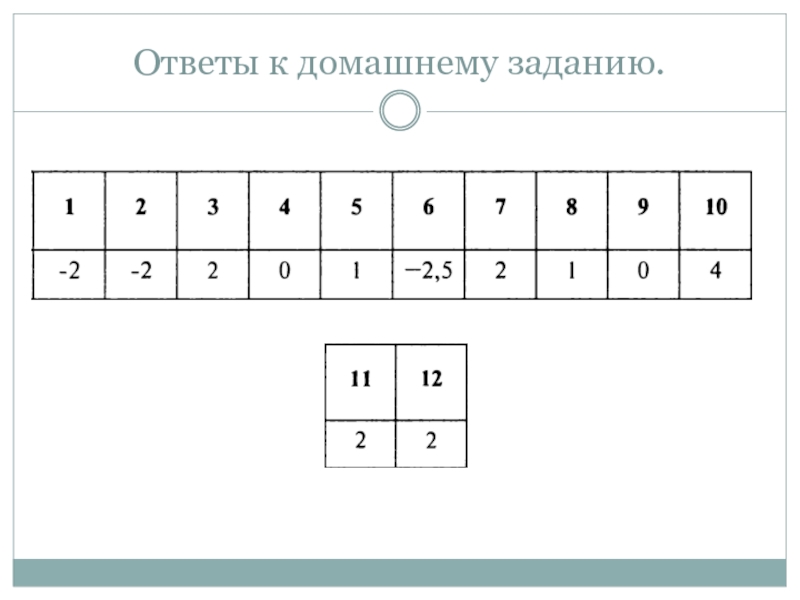
- 3. Ответы к домашнему заданию.
- 4. Решить уравнения.
- 5. Введем новую переменнуюВернемся к старой переменной, решив уравнения:нет решений(т.к. -3 < 0)1)2)
- 6. В скобках записывается результат деления на то
- 7. Введем новую переменнуюВернемся к старой переменной1)2)и выполнить сокращение в скобках
- 8. Свойства:Область определения: множество R действительных чисел.Множество значений:
- 9. Ещё раз рассмотрим уравнение вида a х
- 10. Системы показательных уравненийРешить системуИз первого уравнения выразим
- 11. Системы показательных уравненийРешить системуОчевидно, что основанием обоих
- 12. Решить системы.
- 13. Домашнее задание.
- 14. Скачать презентанцию
Проверка домашнего задания.
Слайды и текст этой презентации
Слайд 5Введем новую переменную
Вернемся к старой переменной, решив уравнения:
нет решений
(т.к. -3
< 0)
Слайд 6В скобках записывается результат деления на то выражение, что выносим
за скобки, а при делении показатели степеней вычитаются.
Вынесем за скобки
общий множитель – степень с меньшим показателем: .Разделим обе части уравнения на (-3)
Слайд 8Свойства:
Область определения: множество R действительных чисел.
Множество значений: множество R всех
положительных действительных чисел.
Монотонность:
Показательная функция
Функция вида
(где a>0, a ≠1) называется показательной функцией с основанием a.основание
a > 1
основание
0 < a < 1
При основании a > 1 функция является возрастающей.
При основании 0 < a < 1 функция является убывающей.