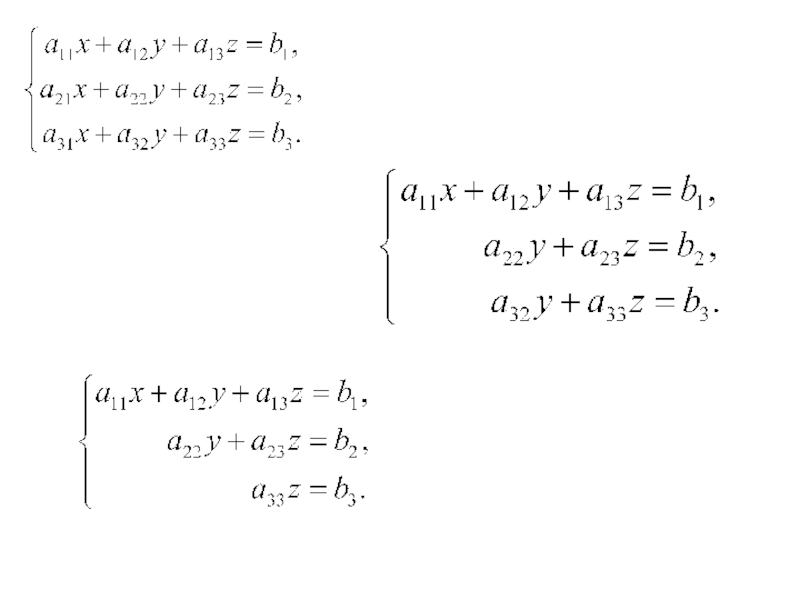Решение систем линейных уравнений с тремя переменными

Содержание

1. Решение систем линейных уравнений с тремя переменными
2. «На пути к истине мыпочти всегда обреченысовершать
3. Слайд 3
4. Метод ГауссаМетод Гаусса решения системы n линейных уравнений с n переменнымипредставляет систематизированную схему последовательного исключенияпеременных
5. Слайд 5
6. Применяя метод Гаусса, решить систему уравнений
7. Применяя метод Гаусса, решить систему уравнений
8. Гаусс Карл ФридрихРодился в семье водопроводчика.С 1795
9. Формулы Крамераиспользование теории определителейГлавный определитель системыВспомогательные определители системы:
10. Слайд 10
11. Слайд 11
12. Решить систему уравнений по формуламКрамераx=0, y=0, z=1
13. Решить систему уравнений по формуламКрамераСистема имеет бесконечно много решений
14. Габриэль Крамер Родился в семье франкоязычного врача.В
15. Самостоятельная работа123
16. 1. x=2,
17. Слайд 17
18. Домашнее задание. Решить систему уравнений двумя способами:
19. Понравился ли тебе урок?Что не понравилось на
20. «Идите, идите вперёд,уверенность придёт к вампозже».
21. Скачать презентанцию

«На пути к истине мыпочти всегда обреченысовершать ошибки».

Главная
Алгебра
Решение систем линейных уравнений с тремя переменными

Слайды и текст этой презентации

Слайд 1Муниципальное общеобразовательное учреждение лицей №1 г. Морозовск
Учитель математики Васецкая Т.С.
19.

10. 2010.
Решение систем линейных
уравнений с тремя переменными

Муниципальное общеобразовательное учреждение лицей №1 г. МорозовскУчитель математики Васецкая Т.С.19. 10. 2010.Решение систем линейныхуравнений с тремя переменными

Слайд 2«На пути к истине мы
почти всегда обречены
совершать ошибки».

(Дени Дидро)

Слайд 3

План урока

Организационный момент

Постановка цели урока

Актуализация знаний

- представление известных личностей из прошлого

4. Самостоятельная работа

5. Итог урока

6. Домашнее задание

7. Рефлексия

Слайд 4Метод Гаусса
Метод Гаусса решения системы n линейных уравнений с n

переменными
представляет систематизированную схему последовательного исключения
переменных

Метод ГауссаМетод Гаусса решения системы n линейных уравнений с n переменнымипредставляет систематизированную схему последовательного исключенияпеременных

Слайд 6Применяя метод Гаусса, решить систему уравнений

Слайд 7Применяя метод Гаусса, решить систему уравнений

Слайд 8Гаусс Карл Фридрих
Родился в семье водопроводчика.
С 1795 по 1798 учился

в Гёттингенском университете.
В 1799 получил доцентуру в Брауншвейге.

В 1807 —

кафедру математики и астрономии в Гёттингенском университете,
с которой была также связана должность директора Гёттингенской
астрономической обсерватории. На этом посту Гаусс оставался до конца жизни.

Отличительными чертами творчества Гаусса являются глубокая органическая
связь в его исследованиях между теоретической и прикладной математикой,
необычайная широта проблематики. Работы Гаусса оказали большое влияние на
развитие высшей алгебры, теории чисел, дифференциальной геометрии.

Гаусс Карл ФридрихРодился в семье водопроводчика.С 1795 по 1798 учился в Гёттингенском университете.В 1799 получил доцентуру в

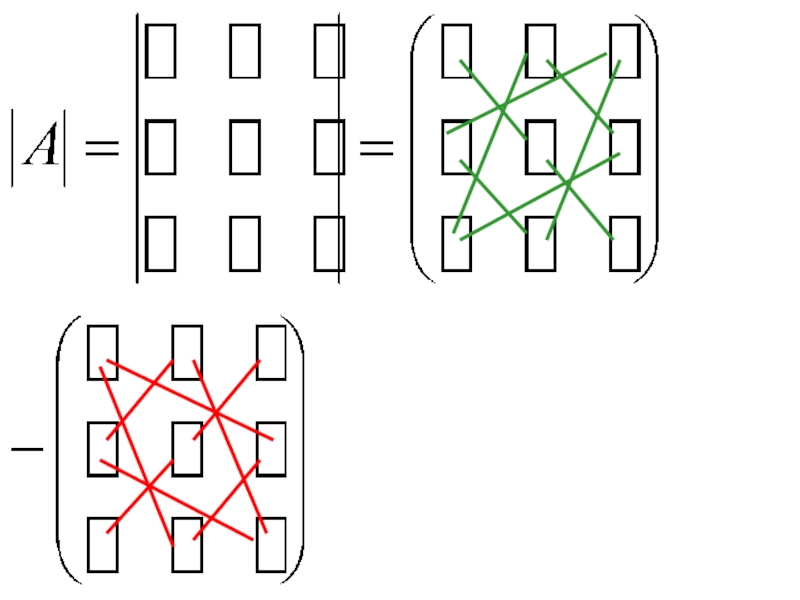
Слайд 9Формулы Крамера
использование теории определителей
Главный определитель системы
Вспомогательные определители системы:

Слайд 10

Слайд 11

Слайд 12Решить систему уравнений по формулам
Крамера
x=0, y=0,

z=1

Решить систему уравнений по формуламКрамераx=0, y=0, z=1

Слайд 13Решить систему уравнений по формулам
Крамера
Система имеет бесконечно много решений

Слайд 14Габриэль Крамер
Родился в семье франкоязычного врача.

В 18 лет защитил

диссертацию.

В 20-летнем возрасте Крамер выставил свою кандидатуру на вакантную должность
преподавателя

на кафедре философии Женевского университета.

Самая известная из работ Крамера — «Введение в анализ алгебраических кривых»
Для доказательства Крамер строит систему линейных уравнений и решает её с
помощью алгоритма, названного позже его именем: метод Крамера