Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразования графиков функций 10 класс
Содержание
- 1. Преобразования графиков функций 10 класс
- 2. ABCxy011В качестве исходного графика функции y=f(x) выберем
- 3. ABCxyI. y=f(x)+a, где a∈.110В новой формуле значения
- 4. ABCxyI. y=f(x)+a, где a∈.110Понятие «параллельного переноса вдоль
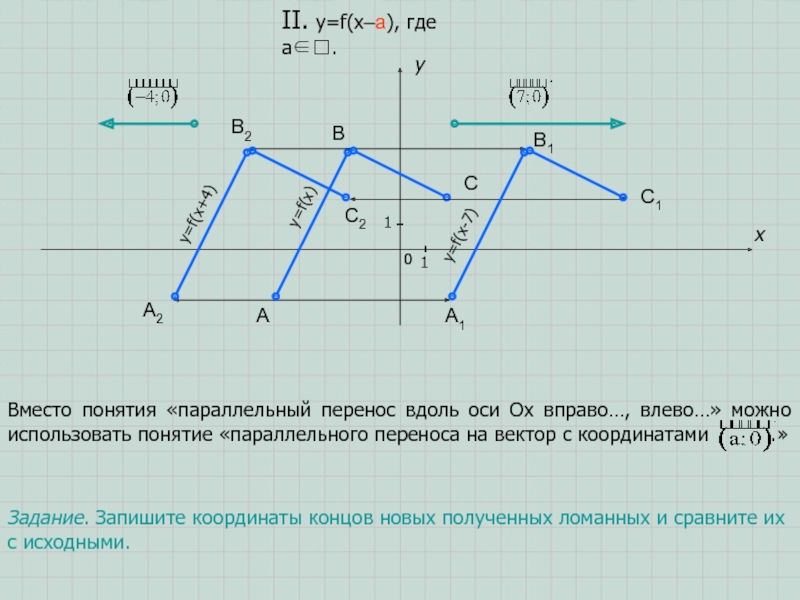
- 5. ABCxy011II. y=f(x–a), где a∈.В новой формуле значения
- 6. ABCxy011II. y=f(x–a), где a∈.Вместо понятия «параллельный перенос
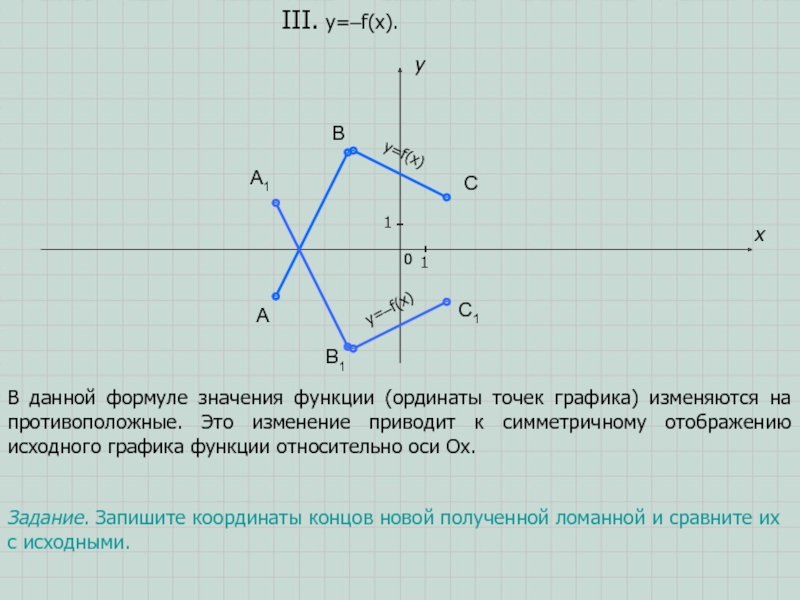
- 7. ABCxyIII. y=–f(x).011A1B1C1В данной формуле значения функции (ординаты
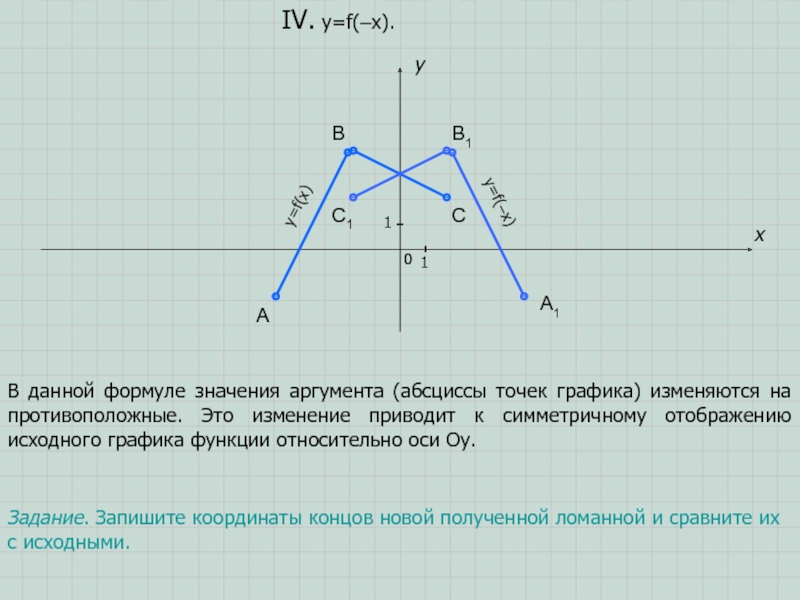
- 8. ABCxy011IV. y=f(–x).В данной формуле значения аргумента (абсциссы
- 9. ABCxy011V. y=k⋅f(x), k>0.В новой формуле значения функции
- 10. ABCxy011VI. y=f(k⋅x), k>0.В новой формуле значения аргумента
- 11. ABCxy011VII. y=|f(x)|.Задание. Запишите координаты концов новой полученной
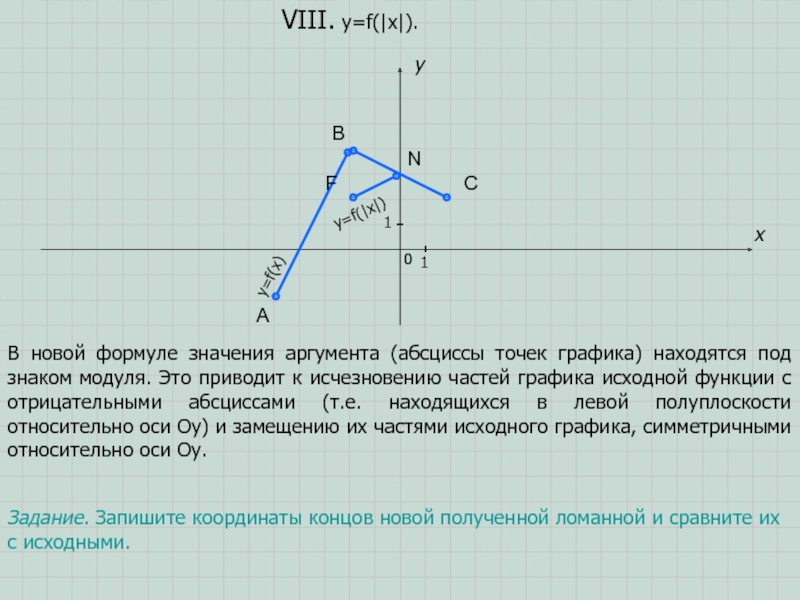
- 12. ABCxy011VIII. y=f(|x|).Задание. Запишите координаты концов новой полученной
- 13. x011yРассмотрим несколько примеров применения вышеизложенной теории.ПРИМЕР 1. Построить график функции, заданной формулой
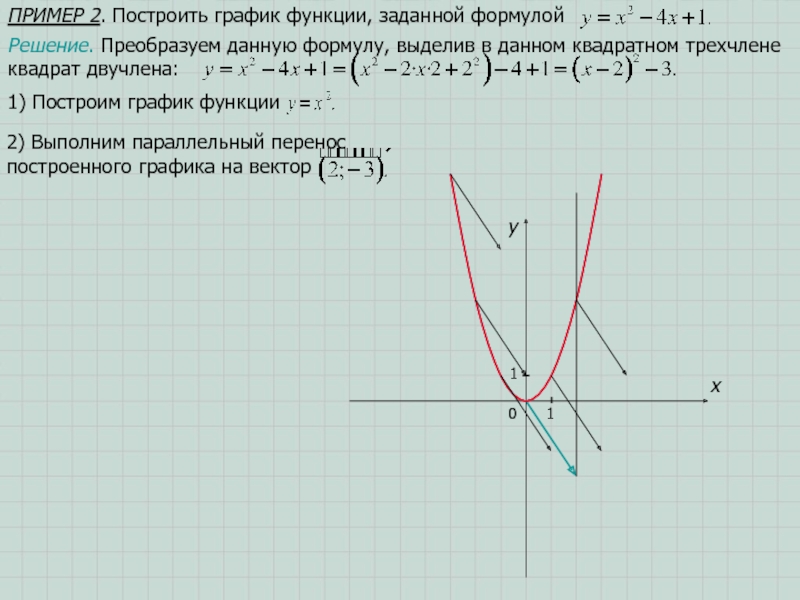
- 14. ПРИМЕР 2. Построить график функции, заданной формулой x1y01
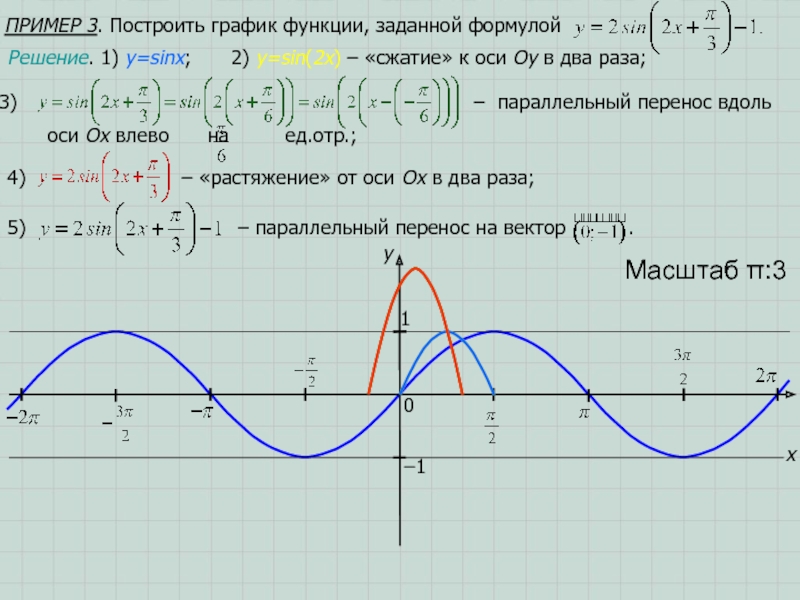
- 15. ПРИМЕР 3. Построить график функции, заданной формулой
- 16. xy10Масштаб π:3−1Остается воспользоваться свойством периодичности любой тригонометрической
- 17. Скачать презентанцию
ABCxy011В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2).Рассмотрим случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию.
Слайды и текст этой презентации
Слайд 1Преобразования графиков функций.
Алгебра и начала анализа, 10 класс.
Воробьев Леонид Альбертович,
г.Минск
Слайд 2A
B
C
x
y
0
1
1
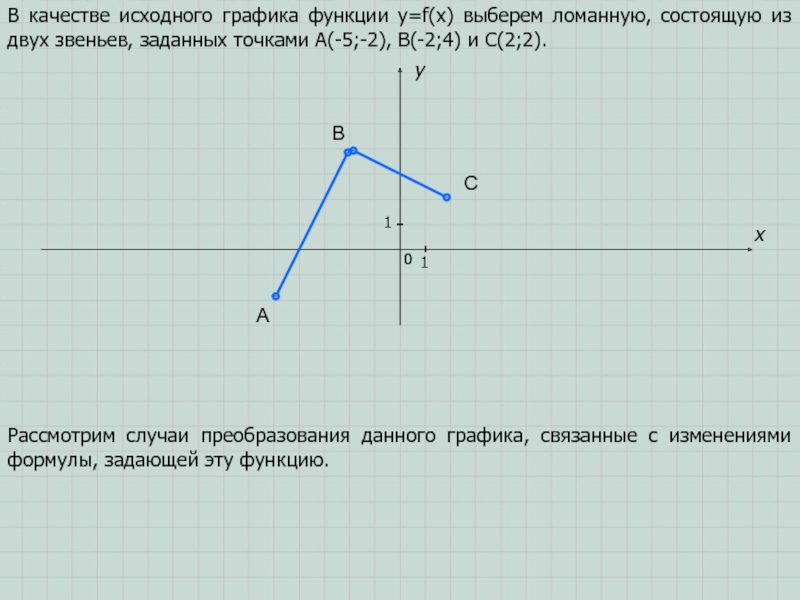
В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из
двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2).
Рассмотрим случаи преобразования
данного графика, связанные с изменениями формулы, задающей эту функцию.
Слайд 3A
B
C
x
y
I. y=f(x)+a, где a∈.
1
1
0
В новой формуле значения функции (ординаты точек
графика) изменяются на число a, по сравнению со «старым» значением
функции. Это приводит к параллельному переносу графика функции вдоль оси Oy:вверх на a ед.отр., если a>0 или
вниз на a ед.отр., если a<0.
Например:
1) y=f(x)+3;
A1
B1
C1
y=f(x)
y=f(x)+3
или 2) y=f(x)–2.
A2
B2
C2
y=f(x)-2
Слайд 4A
B
C
x
y
I. y=f(x)+a, где a∈.
1
1
0
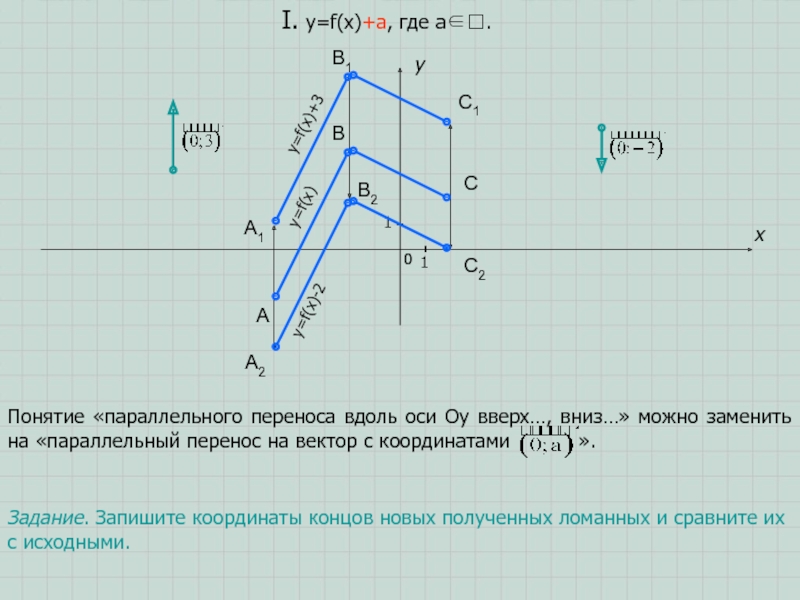
Понятие «параллельного переноса вдоль оси Oy вверх…,
вниз…» можно заменить на «параллельный перенос на вектор с координатами
».A1
B1
C1
y=f(x)
y=f(x)+3
A2
B2
C2
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
y=f(x)-2
Слайд 5A
B
C
x
y
0
1
1
II. y=f(x–a), где a∈.
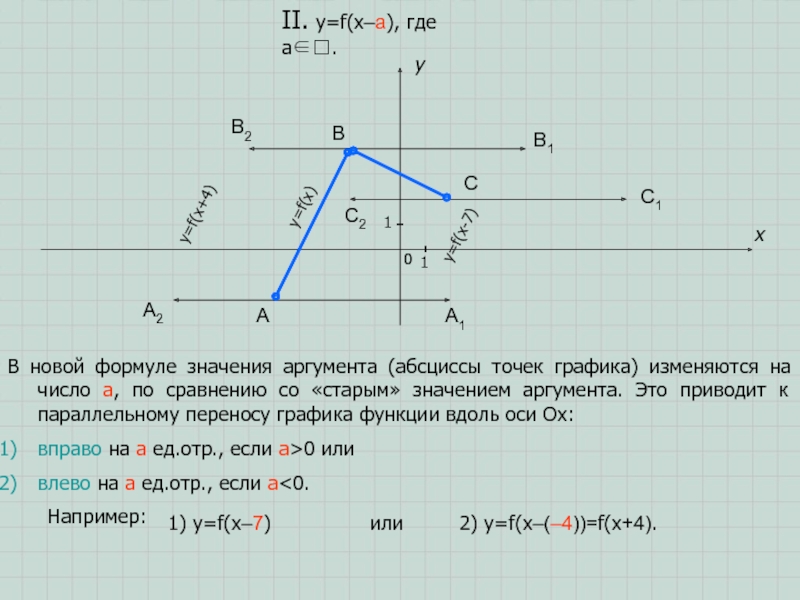
В новой формуле значения аргумента (абсциссы точек
графика) изменяются на число a, по сравнению со «старым» значением
аргумента. Это приводит к параллельному переносу графика функции вдоль оси Ox:вправо на a ед.отр., если a>0 или
влево на a ед.отр., если a<0.
Например:
1) y=f(x–7)
y=f(x)
y=f(x-7)
A1
B1
C1
или 2) y=f(x–(–4))=f(x+4).
A2
B2
C2
y=f(x+4)
Слайд 6A
B
C
x
y
0
1
1
II. y=f(x–a), где a∈.
Вместо понятия «параллельный перенос вдоль оси Oх
вправо…, влево…» можно использовать понятие «параллельного переноса на вектор с
координатами .»y=f(x)
y=f(x-7)
A1
B1
C1
A2
B2
C2
y=f(x+4)
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
Слайд 7A
B
C
x
y
III. y=–f(x).
0
1
1
A1
B1
C1
В данной формуле значения функции (ординаты точек графика) изменяются
на противоположные. Это изменение приводит к симметричному отображению исходного графика
функции относительно оси Ох.Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=–f(x)
Слайд 8A
B
C
x
y
0
1
1
IV. y=f(–x).
В данной формуле значения аргумента (абсциссы точек графика) изменяются
на противоположные. Это изменение приводит к симметричному отображению исходного графика
функции относительно оси Оу.A1
B1
C1
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=f(–x)
Слайд 9A
B
C
x
y
0
1
1
V. y=k⋅f(x), k>0.
В новой формуле значения функции (ординаты точек графика)
изменяются в k раз, по сравнению со «старым» значением функции.
Это приводит к :«растяжению» графика функции от оси Oх в k раз, если k>1 или
«сжатию» графика функции к оси Ох в раз, если k<1.
Например:
1) y=2⋅f(x);
или 2) y=0,5⋅f(x).
A1
B1
C1
y=f(x)
y=2⋅f(x)
A2
B2
C2
y=0,5⋅f(x)
Если k<0, то данный случай комбинируют с III.
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
Слайд 10A
B
C
x
y
0
1
1
VI. y=f(k⋅x), k>0.
В новой формуле значения аргумента (абсциссы точек графика)
изменяются в k раз, по сравнению со «старым» значением аргумента.
Это приводит к :1) «растяжению» графика функции от оси Oу в раз, если k<1 или
2) «сжатию» графика функции к оси Оу в k раз, если k>1.
Например:
Если k<0, то данный случай комбинируют с IV.
1) y=f(0,5⋅x);
или 2) y=f(2⋅x).
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
A1
B1
C1
A2
B2
C2
y=f(x)
y=f (0,5⋅x)
y=f(2⋅x)
Слайд 11A
B
C
x
y
0
1
1
VII. y=|f(x)|.
Задание. Запишите координаты концов новой полученной ломанной и сравните
их с исходными.
В новой формуле значения функции (ординаты точек графика)
находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными ординатами (т.е. находящихся в нижней полуплоскости относительно оси Ох) и симметричному отображению этих частей относительно оси Ох.A1
M
Вспомните определение
модуля:
y=f(x)
y=|f(x)|
Слайд 12A
B
C
x
y
0
1
1
VIII. y=f(|x|).
Задание. Запишите координаты концов новой полученной ломанной и сравните
их с исходными.
В новой формуле значения аргумента (абсциссы точек графика)
находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными абсциссами (т.е. находящихся в левой полуплоскости относительно оси Оу) и замещению их частями исходного графика, симметричными относительно оси Оу.N
F
y=f(x)
y=f(|x|)
Слайд 13x
0
1
1
y
Рассмотрим несколько примеров применения вышеизложенной теории.
ПРИМЕР 1. Построить график функции,
заданной формулой
Слайд 15ПРИМЕР 3. Построить график функции, заданной формулой
x
y
1
0
Масштаб π:3
−1
Решение. 1)
y=sinx;
2) y=sin(2x) – «сжатие» к оси Оу в два раза;
Слайд 16x
y
1
0
Масштаб π:3
−1
Остается воспользоваться свойством периодичности любой тригонометрической функции (определите наименьший
положительный период самостоятельно) и достроить полученную часть до полного графика
на всей числовой оси:
Теги
