Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Иррациональные числа
Содержание
- 1. Иррациональные числа
- 2. Устно1) -8; 2,1; 7;
- 3. Решить уравнение: х(х-5)=0;
- 4. Подумай!Равна ли нулю дробь?2. Вычисли устно:
- 5. Слайд 5
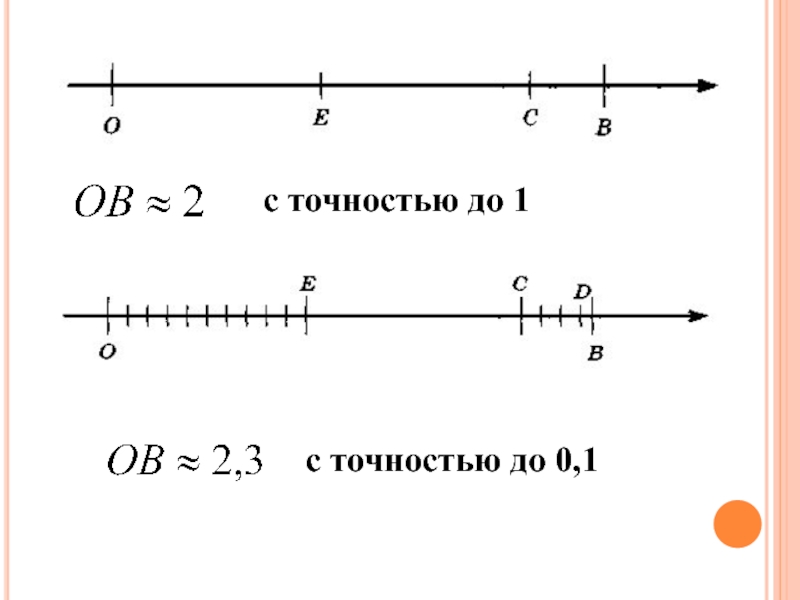
- 6. Бесконечная десятичная дробь
- 7. Слайд 7
- 8. При десятичном измерении отрезка ОК получится бесконечная
- 9. Числа, которые не являются рациональными, то есть
- 10. Действительные числа Q
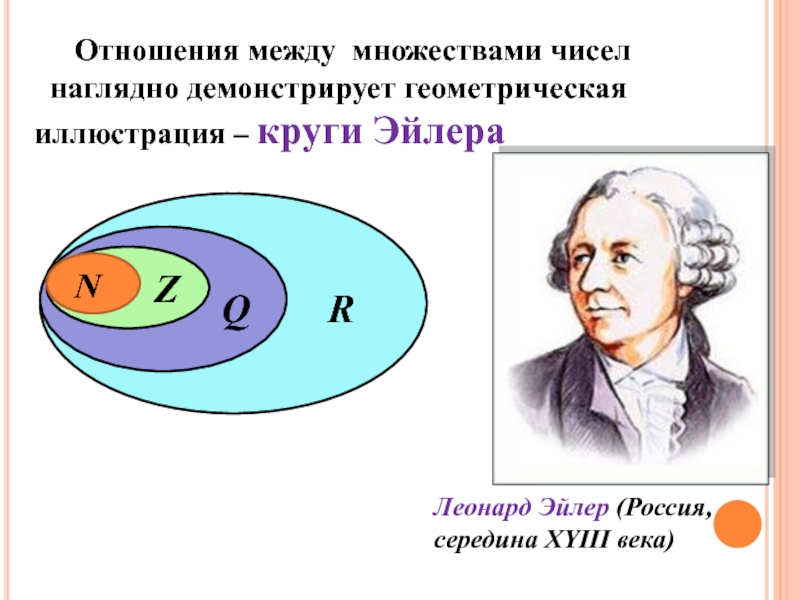
- 11. Леонард Эйлер (Россия, середина XYΙΙΙ века) Отношения между множествами чисел наглядно демонстрирует геометрическая иллюстрация – круги ЭйлераNZQR
- 12. Скачать презентанцию
Устно1) -8; 2,1; 7; ; 3,(6); 0; 201; ; -1; 4,2(32) 2)
Слайды и текст этой презентации
Слайд 1
Иррациональные числа
Соловей Татьяна Александровна,
учитель математики МОУ СОШ № 1
с.Екатеринославка
Слайд 2Устно
1) -8; 2,1; 7; ; 3,(6);
0; 201; ; -1; 4,2(32)
2) ; - 3,25;
3) 0,125 и 0,038; -2,45 и -2,54; и ;
5,73 и 5,(73); -1,53 и -1,(53); -1,(53) и -1,(35)
4) округлить 13, 509276
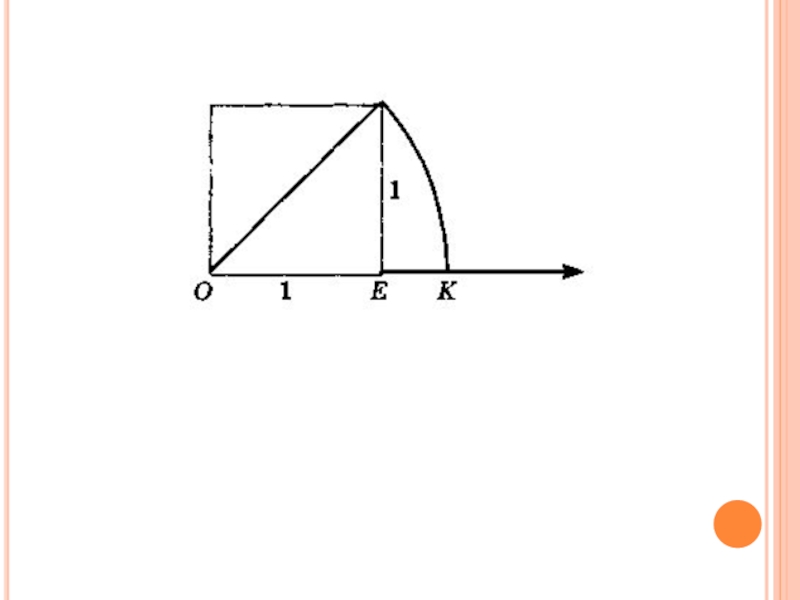
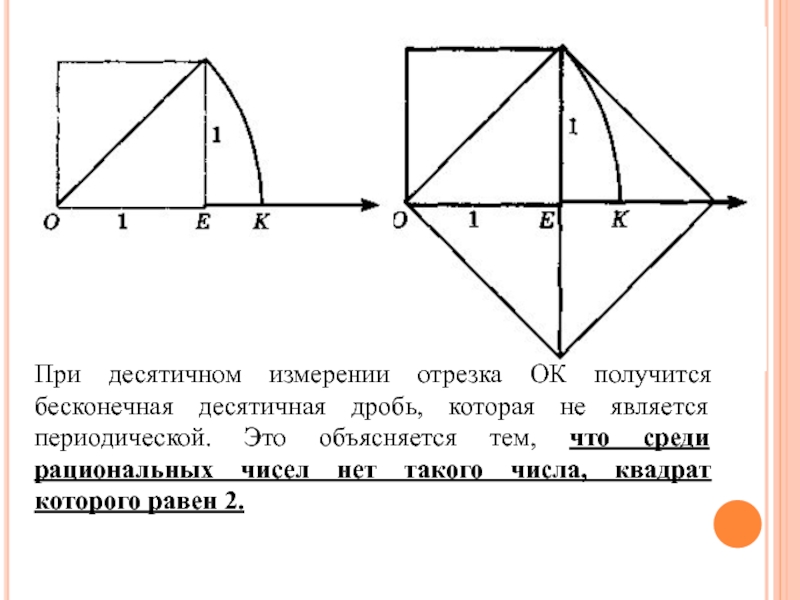
Слайд 8При десятичном измерении отрезка ОК получится бесконечная десятичная дробь, которая
не является периодической. Это объясняется тем, что среди рациональных чисел
нет такого числа, квадрат которого равен 2.Слайд 9Числа, которые не являются рациональными, то есть не являются ни
целыми, ни представимыми в виде
дроби вида , где
m – целое число, а n – натуральное, называются иррациональными.
Изученные множества чисел обозначаются следующим образом:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.