Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение уравнений и неравенств, содержащих модуль, методом интервалов
Содержание
- 1. Решение уравнений и неравенств, содержащих модуль, методом интервалов
- 2. Модулем действительного числа а ( |а| )
- 3. № 1. Решить уравнение: |х+2| = |х-1| + х-3
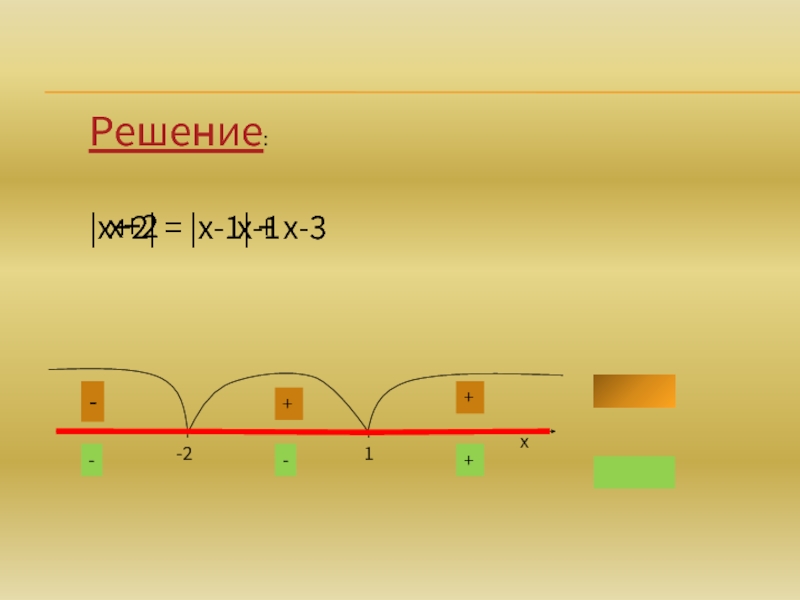
- 4. Решение:|х+2| = |х-1| + х-3=0 при х=-2 =0 при х=1х+2х-1-21
- 5. Решение:|х+2| = |х-1| + х-3-21хх+2х-1--+-++
- 6. Решение:|х+2| = |х-1|+х-3х-х-2=-х+1+х-3 х=2 – не удовлетворяет условию х
- 7. решений нетрешений нет х=6Ответ: х=6
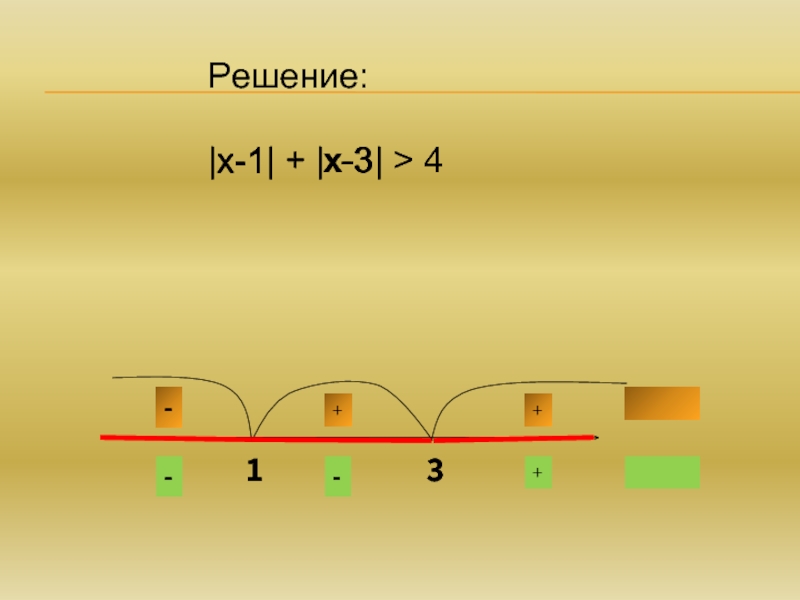
- 8. №2. Решить неравенство: |х-1| + |х-3| > 4
- 9. Решение:|х-1| + |х-3| > 4х-1х-3= 0 при х=1=0 при х=313
- 10. -+++--Решение:|х-1| + |х-3| > 4х-1х-3
- 11. Решение: |х-1| + |х-3| > 4Если х 4-х+1
- 12. Общий алгоритмнайти нули подмодульных выражений и отметить
- 13. Большое количество ошибок при решении задач с
- 14. Поэтому при решении задач, в которые входят два или более модулей, рекомендуется использовать метод интервалов.
- 15. Конец
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Решение
уравнений и неравенств,
содержащих модуль,
методом интервалов
Трескина Виктория Борисовна,
школа №
594
Слайд 2
Модулем действительного числа а ( |а| ) называется:
само это
число, если а – положительное число;
нуль, если число а –
нуль;число, противоположное а , если число а – отрицательное.
Или
а, если а>0
0, если а=0
-а, если а<0
|а| =
Определение модуля
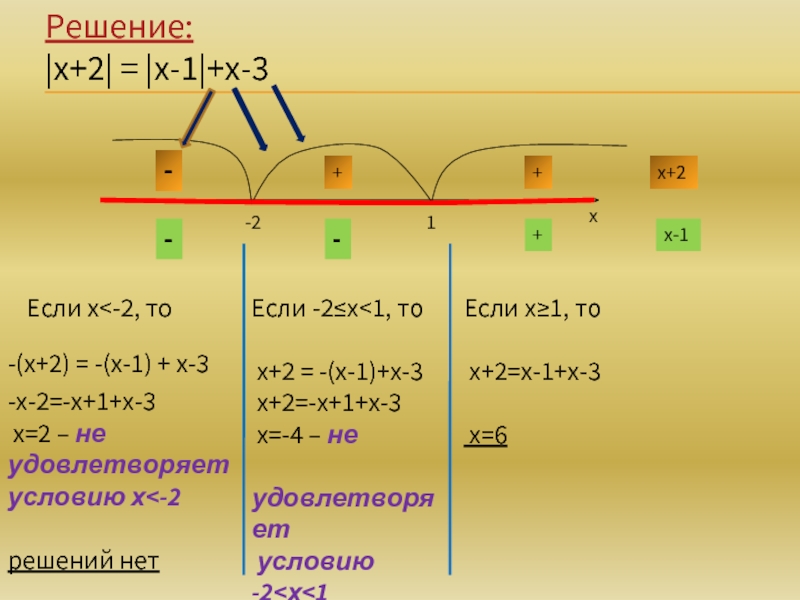
Слайд 6Решение:
|х+2| = |х-1|+х-3
х
-х-2=-х+1+х-3
х=2 – не удовлетворяет
условию х
-2≤х
условию -2<х<1решений нет
Если х≥1, то
х+2=х-1+х-3
х=6
Если х<-2, то
-(х+2) = -(х-1) + х-3
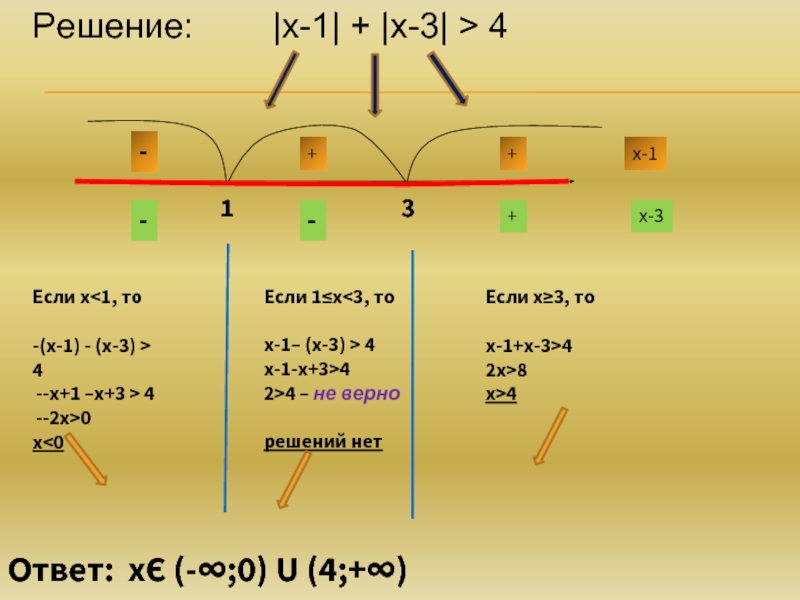
Слайд 11Решение: |х-1| + |х-3| > 4
Если х
4
-х+1 –х+3 > 4
-2х>0
х4
2>4 –
не вернорешений нет
Если х≥3, то
х-1+х-3>4
2х>8
х>4
Ответ: хЄ (-∞;0) U (4;+∞)
Слайд 12Общий алгоритм
найти нули подмодульных выражений и отметить их на числовой
прямой
определить знаки подмодульных выражений на полученных промежутках
на каждом
промежутке решить уравнение ( неравенство ) объединить полученные решения




















![[гъ] ,[г]авазлары һәм Г,г хәрефләре 1 класс](/img/thumbs/6c7bfeb483d73759446a8dff9cbd1db1-800x.jpg)







