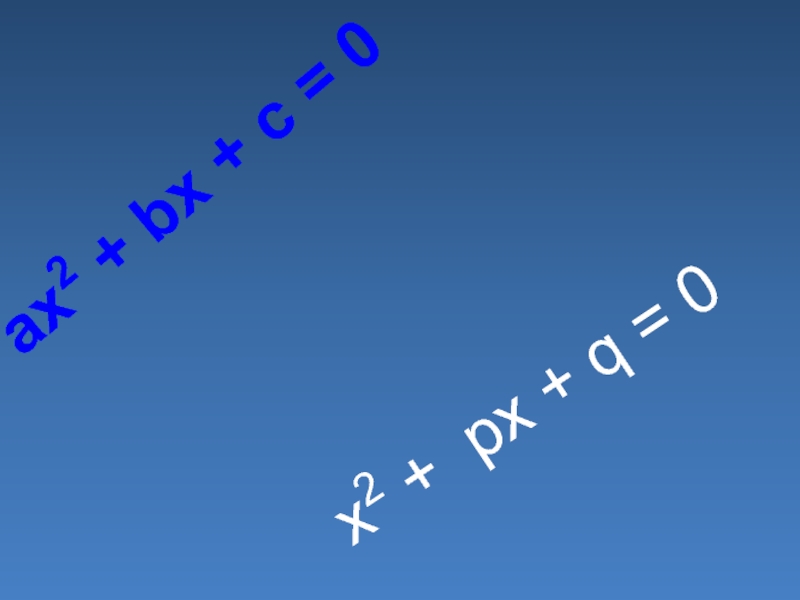Способы решения квадратных уравнений

уравнений
x2 + px + q = 0

0. Разложим левую часть уравнения на множители применив способ группировки:
х

2 +10 х – 24 = х 2 + 12 х - 2 х – 24 = х (х + 12) - 2(х + 12) = (х + 12)( х - 2).
Уравнение можно переписать так:
(х + 12)( х - 2) = 0
Произведение равно нулю, когда один из его множителей равен нулю. Левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. Значит, числа 2 и -12 являются корнями уравнения
х 2 +10 х – 24 = 0.

0.
Выделим в левой части полный квадрат. Для этого запишем выражение

х2 + 6х в следующем виде:
х 2 + 6х = х2 + 2 х *3.
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. Поэтому чтобы получить полный квадрат, нужно прибавить 9 , так как
х2 + 2х*3 + 9 = (х + 3)2
Преобразуем теперь левую часть уравнения:
х2+ 6х- 7 = 0,
Прибавляя к ней и вычитая 9. Имеем:
х 2 + 6 х – 7 = х2 + 2 х *3 + 9 – 9 – 7 = (х + 3)2 – 9 – 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 – 16 = 0, т.е. (х + 3)2 = 16.
Следовательно, х + 3=4, х = 1, или х + 3= - 4, х = - 7.

q = 0
Его корни удовлетворяют теореме Виета, которая при a

= 1 имеет вид
x1 x2 = q
x1 + x2 = -p
Отсюда можно сделать следующие выводы
a) Если свободный член q приведённого уравнения положителен (q>0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p. Если p>0, то оба корня отрицательны, если p<0, то оба корня положительны.
b) Если свободный член q приведённого уравнения отрицателен (q<0), то уравнение имеет два различных по знаку корня, причём больший по модулю корень будет положителен, если p<0, или отрицателен, если p>0.

0, где а 0.
Если a + b + c

= 0, то х1 = 1, х2 = с/а.
Доказательство. Разделим обе части уравнения на а, получим приведённое квадратное уравнение
x + bx/a + c/a = 0.
Согласно теореме Виета
x1 + х2 = (-b)/a,
x1x2 = c/a,
По условию a + b + c = 0, откуда b = -a -c. Значит,
x1+x2= -(-a - c)/a = 1 + c/a,
x1x2=1c/a.
Получаем х1 = 1, х2 = с/а, что и требовалось дoказать.
Если a – b + c = 0,или b = a + c, то х1 = -1, х2 = -с/а
Доказательство. По теореме Виета
x1 + х2 = (-b)/a,
x1x2 = -1(-c/a),
По условию a – b + c = 0, откуда b = a + c. Таким образом
x1+х2 = -(a + b)/a = -1 - c/a,
x1x2 = -1(-c/a),
т.е х1 = -1 и х2 = -с/а, что и требовалось доказать.