Тригонометрические уравнения

точек числовой
окружности;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и

1) уметь отмечать точки на числовой
окружности;

3) знать свойства основных
тригонометрических функций;

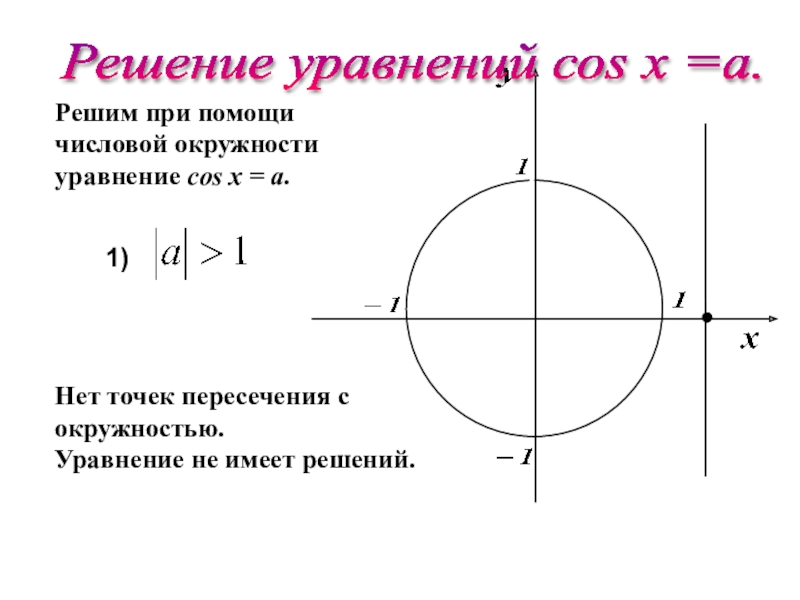
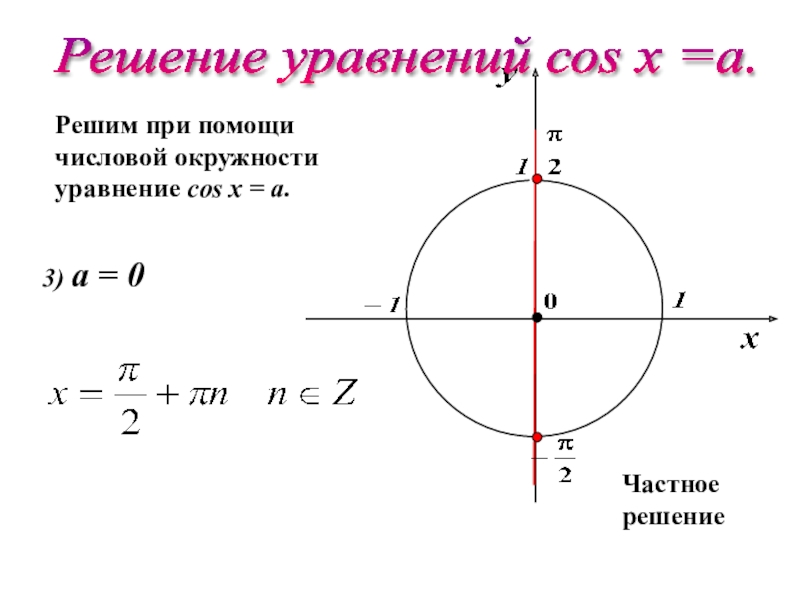
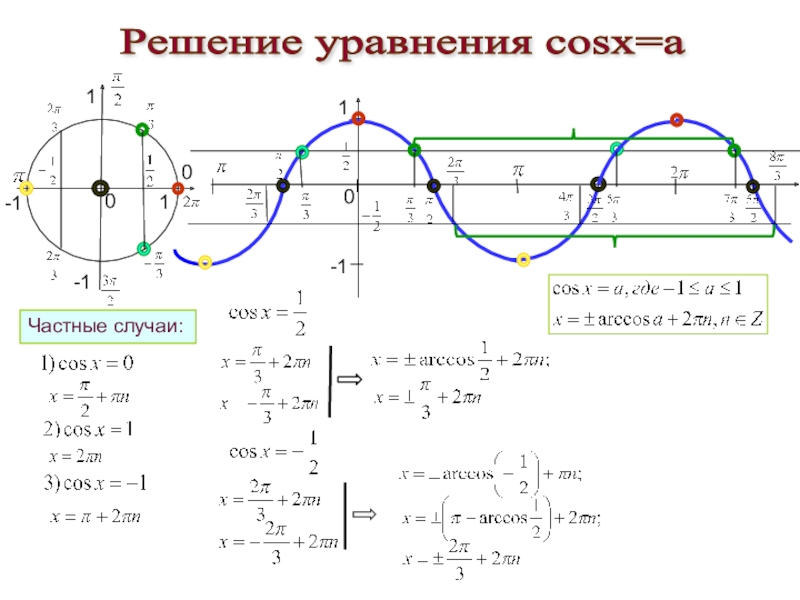
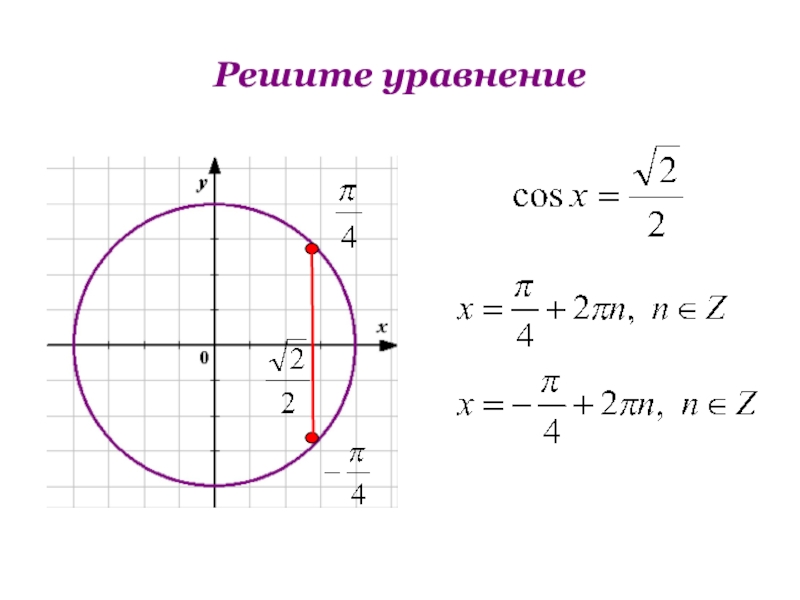
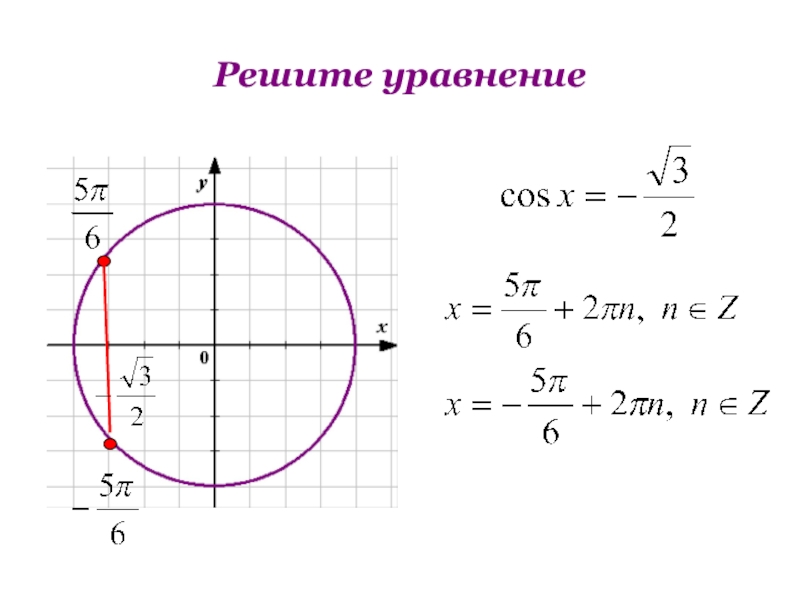
Чтобы успешно решать простейшие
тригонометрические уравнения нужно

соответствующей числу

точки; укажите три угла поворота, в результате которых начальная точка

М

точки; укажите три угла поворота, в результате которых начальная точка

М

[0;π ], косинус которого равен а

а
arccos (-a)= π -arccos a

-а

π-arccos

Арккосинус и решение уравнений соs х=a.

пересечения с окружностью.
Уравнение не имеет решений.

Решение уравнений соs х =a.

1
х = 2πk


cos х = -1
х = π+2πk

Частные решения

Решение уравнений

0


Частное решение
Решение уравнений соs х =a.

а
-arccos а
Корни, симметричные относительно Оx могут быть записаны:

х = ±

или

а

Решение уравнений соs х =a.

Отметить точку а на оси абсцисс (линии косинусов)
3. Провести перпендикуляр

4. Отметить точки пересечения перпендикуляра с окружностью.

5. Полученные числа– решения уравнения cosх = a.

6. Записать общее решение уравнения.

1. Проверить условие | a | ≤ 1

a

х1

-х1

-1

1

Решается с помощью единичной окружности

Может ли arccos a принимать значение
3) Вычислите

уравнение:
2. Вычислить