Разделы презентаций

Замечательные кривые 8 класс

Содержание

Линии в природе© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Слайды и текст этой презентации

Слайд 1Преподаватель математики
Куткина О.А.
Замечательные кривые

Преподаватель математики Куткина О.А.Замечательные кривые

Слайд 2Линии в природе
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Линии в природе© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Слайд 3Замечательные кривые
К кривым математическая наука обратилась только в 17 веке,

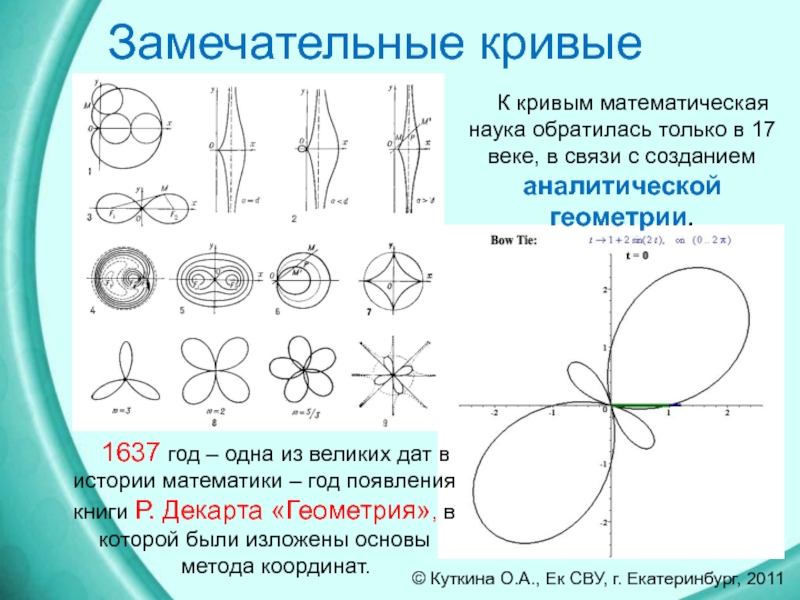
в связи с созданием аналитической геометрии.
1637 год – одна из

великих дат в истории математики – год появления книги Р. Декарта «Геометрия», в которой были изложены основы
метода координат.

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Замечательные кривыеК кривым математическая наука обратилась только в 17 веке, в связи с созданием аналитической геометрии.1637 год

Слайд 4Окружность
Парабола
Гипербола
Конические сечения
открыты греками
Эллипс
© Куткина О.А., Ек СВУ, г. Екатеринбург,

2011

ОкружностьПараболаГиперболаКонические сечения открыты грекамиЭллипс© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Слайд 5Название "Эллипс" ввёл Аполлоний Пергский, рассматривая эллипс
как одно из

конических сечений.
Все точки эллипса, как видно из построения, обладают одним

свойством: 

Эллипс

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Название

Слайд 6Спираль Архимеда
Идея
движения
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Спираль АрхимедаИдея движения© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Слайд 7Лемниската
Бернулли
Название происходит от греч. λημνισχος — лента, повязка. В Древней

Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к

голове победителя на спортивных играх.

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

ЛемнискатаБернуллиНазвание происходит от греч. λημνισχος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого

Слайд 8Кардиоида
Идея
движения
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011
Траектория движения

точки, закрепленной на окружности, катящейся с внешней стороны по другой

окружности того же радиуса, называется кардиоидой.

Греческое слово «кардио» означает «сердце»

КардиоидаИдея движения© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011Траектория движения точки, закрепленной на окружности, катящейся с внешней

Слайд 9Улитка Паскаля
Лимакона была открыта французским математиком Этьеном Паскалем
(отцом знаменитого

ученого
Блеза Паскаля)
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011
Удлиненная

кардиоида
Улитка ПаскаляЛимакона была открыта французским математиком Этьеном Паскалем (отцом знаменитого ученого Блеза Паскаля)© Куткина О.А., Ек СВУ,

Слайд 10История исследования циклоиды связана с именами таких великих учёных, философов,

математиков и физиков, как Аристотель, Птолемей, Галилей, Гюйгенс, Торичелли и

др.

Циклоида

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Идея
движения

История исследования циклоиды связана с именами таких великих учёных, философов, математиков и физиков, как Аристотель, Птолемей, Галилей,

Слайд 11Гипоциклоиды
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011
Все кривые, которые

вычерчивает точка на окружности, катящейся внутри другой окружности, принадлежит семейству

гипоциклоид
(от греческого «гипо» - «под», «внизу»
и «киклоидес» - «кругообразный»).

Идея
движения

Гипоциклоиды© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011Все кривые, которые вычерчивает точка на окружности, катящейся внутри другой

Слайд 12Кривая Штейнера
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011
Траектория движения

точки, закрепленной на окружности, катящейся внутри другой окружности в 3

раза большего радиуса, называется кривой Штейнера.

Астроида

Траектория движения точки, закрепленной на окружности, катящейся внутри другой окружности в 4 раза большего радиуса, называется астроидой.

Кривая Штейнера© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011Траектория движения точки, закрепленной на окружности, катящейся внутри другой

Слайд 13Декартов лист
Впервые уравнение кривой исследовал Р. Декарт в 1638 году,

однако он построил только петлю в первом координатном угле, где

x и y принимают положительные значения.

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Декартов листВпервые уравнение кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом

Слайд 14Декарт полагал, что петля симметрично повторяется во всех четырёх координатных

четвертях, в виде четырёх лепестков цветка. В то время эта

кривая называлась цветком жасмина.

Трехлепестковая
роза

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка.

Слайд 15Строфоида
© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011
Эпициклоида
Кривая, которую описывает

точка, закрепленная на окружности, катящейся с внешней стороны по другой

окружности
Строфоида© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011ЭпициклоидаКривая, которую описывает точка, закрепленная на окружности, катящейся с внешней

Слайд 16ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИ
в начертательной геометрии обычно рассматриваются как результат пересечения

поверхностей или траекторию движения точки.
Классическим примером пространственных кривых линий являются

цилиндрическая и коническая винтовые линии.

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИв начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.Классическим примером пространственных

Слайд 17Желаю вам новых открытий!
Источники: 
Нагибин, Ф.Ф., Канин, Е.С.
Математическая шкатулка.

М. - Просвещение, 1988. 
Шарыгин, И.Ф., Ерганжиева, Л.Н.
Наглядная геометрия

5-6. М. - Дрофа, 2000. 
http://sbiryukova.narod.ru 
http://www.rubrikon.ru/qe.asp? 
http://arbuz.narod.ru 
http://www.imp-word-r.narod.ry/articles/escher_math/escher_math_html 

© Куткина О.А., Ек СВУ, г. Екатеринбург, 2011

Желаю вам новых открытий!Источники: Нагибин, Ф.Ф., Канин, Е.С. Математическая шкатулка. М. - Просвещение, 1988. Шарыгин, И.Ф., Ерганжиева,

Похожие презентации

Разложение многочленов на множители. Вынесение общего множителя за скобки 7 класс Разложение многочленов на множители. Вынесение общего множителя за скобки 7 класс 399
Применения матриц в экономике Применения матриц в экономике 592
Графический способ решения уравнений 11 класс Графический способ решения уравнений 11 класс 525
Функция у=ах2 и ее свойства Функция у=ах2 и ее свойства 460
Решение задач с помощью уравнений Алгебра, 7 класс Решение задач с помощью уравнений Алгебра, 7 класс 818
решение показательных уравнений 10 класс решение показательных уравнений 10 класс 321
Решение линеиных неравенств Решение линеиных неравенств 475
Стандартный вид числа Стандартный вид числа 458
Понятия вектора. Равные вектора 8 класс Понятия вектора. Равные вектора 8 класс 354
Преобразование сумм тригонометрических функций в произведение Сумма (разность) синусов Сумма (разность) косинусов Преобразование сумм тригонометрических функций в произведение Сумма (разность) синусов Сумма (разность) косинусов 528
Подобные слагаемые Подобные слагаемые 1154
Формулы для решения квадратного уравнения Формулы для решения квадратного уравнения 445
ВЫСШАЯ МАТЕМАТИКА ПРЕДЕЛЫ. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ВЫСШАЯ МАТЕМАТИКА ПРЕДЕЛЫ. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ 586
Массивы Массивы 336
Логарифмы Логарифмы 606
Проценты в жизни человека. Решение текстовых задач 6 класс Проценты в жизни человека. Решение текстовых задач 6 класс 360
Показательные уравнения 11 класс Показательные уравнения 11 класс 480
Тождества Тождества 551
Тест Тест "Вынесение общего множителя за скобки" 7 класс 446
Перестановки Перестановки 471

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика