Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические задачи типа «С4»
Содержание
- 1. Геометрические задачи типа «С4»
- 2. Задачи Желаю успеха! "Дорогу осилит идущий!" Помните:
- 3. В треугольнике АВС АВ=15, ВС = 12,
- 4. В треугольнике АВС АВ=15, ВС = 12,
- 5. В треугольнике АВС АВ=15, ВС = 12,
- 6. Пусть окружность вписана в треугольник ABC. Тогда
- 7. Точка H – основание высоты треугольника со
- 8. нижнее основание вдвое больше верхнего, BC =
- 9. По условию BC = a, АD =
- 10. По условию BC = 3a, АD =
- 11. №4В параллелограмме ABCD AB=12, биссектрисы углов при
- 12. №4В параллелограмме ABCD AB=12, биссектрисы углов при
- 13. №4В параллелограмме ABCD AB=12, биссектрисы углов при
- 14. http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D1%8B Использованные ресурсыТексты задач взяты с сайта
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Геометрические задачи типа «С4»
по материалам ЕГЭ – 2010
МОУ «Инсарская
средняя общеобразовательная школа №1»
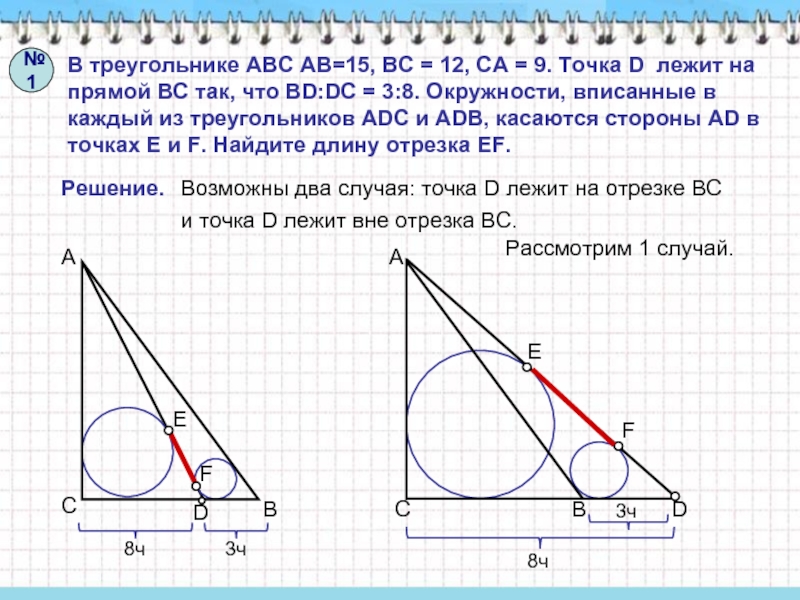
Республика МордовияСлайд 3В треугольнике АВС АВ=15, ВС = 12, СА = 9.
Точка D лежит на прямой ВС так, что BD:DC =
3:8. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.Решение.
Возможны два случая: точка D лежит на отрезке ВС
и точка D лежит вне отрезка ВС.
Рассмотрим 1 случай.
№1
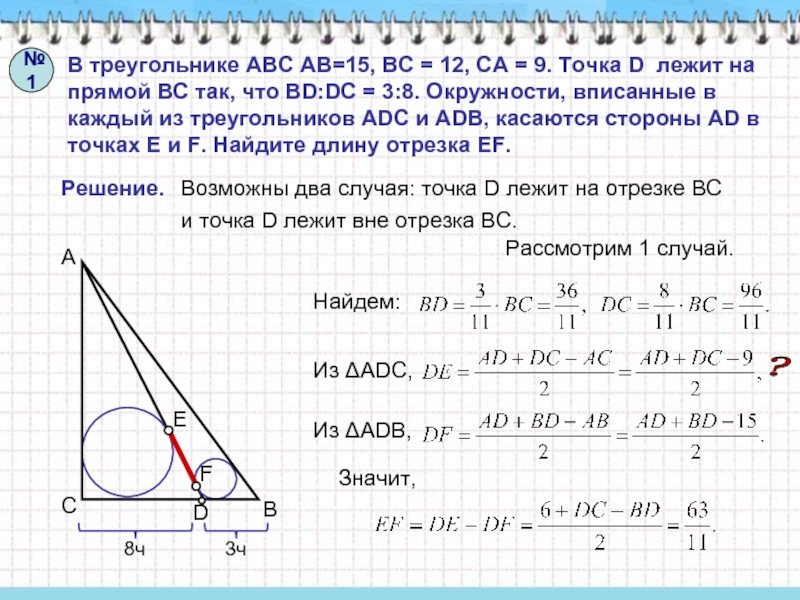
Слайд 4В треугольнике АВС АВ=15, ВС = 12, СА = 9.
Точка D лежит на прямой ВС так, что BD:DC =
3:8. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.Решение.
Возможны два случая: точка D лежит на отрезке ВС
и точка D лежит вне отрезка ВС.
Рассмотрим 1 случай.
Найдем:
Значит,
Из ΔADC,
Из ΔADВ,
№1
?
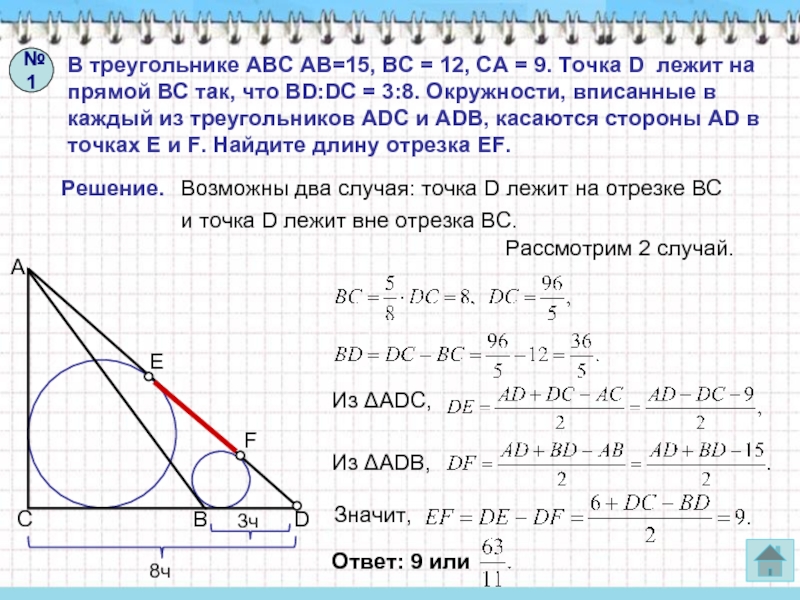
Слайд 5В треугольнике АВС АВ=15, ВС = 12, СА = 9.
Точка D лежит на прямой ВС так, что BD:DC =
3:8. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.Решение.
Возможны два случая: точка D лежит на отрезке ВС
и точка D лежит вне отрезка ВС.
Значит,
Из ΔADC,
Из ΔADВ,
№1
Рассмотрим 2 случай.
Слайд 6Пусть окружность вписана в треугольник ABC. Тогда расстояние от вершины
A до точки касания окружности со стороной AB равно
А
В
С
О
x
x
y
y
z
z
Доказательство.
М
N
К
Мы
знаем, что центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника, значит AM=AK=x, BM=BN=y, CK=CN=z. Тогда, периметр ΔАВС равен: , откуда
или
Вспомогательная задача.
Слайд 7Точка H – основание высоты треугольника со сторонами 10, 12,
14 , опущенной на сторону, равную 12. Через точку H
проведена прямая, отсекающая от треугольника подобный ему треугольник и пересекающая сторону, равную 10, в точке M . Найдите HM .Решение.
Пусть АВ = 10, ВС = 12, АС = 14.
По условию ΔАВС∞ΔНВМ, и имеют общий угол В, значит возможны два случая.
1 случай. ∠ВМН = ∠ВАС;
2 случай. ∠ВМН = ∠АСВ;
ΔАВН – прямоугольный, BН = АВ·cosB = 2.
значит,
, значит,
№2
Слайд 8
нижнее основание вдвое больше верхнего, BC = a, АD =
2a,
верхнее основание вдвое больше нижнего, AD = a, BC =
2a.Площадь трапеции ABCD равна 240. Диагонали пересекаются в точке O , отрезки, соединяющие середину P основания AD с вершинами B и C , пересекаются с диагоналями трапеции в точках M и N . Найдите площадь четырехугольника OMPN , если одно из оснований трапеции втрое больше другого.
Решение.
Возможно два вида трапеции.
Найдем площадь ОMPN:
В обоих случаях:
Рассмотрим первый случай.
№3
SMONP=SΔAOD – SΔAMP – SΔPND.
Слайд 9По условию BC = a, АD = 3a, аh =
120.
1) ΔBOC∞ΔAOD ,
по трем углам
h
2) ΔBMC∞ΔAMP , по трем
углам,Тогда высота треугольника АМР равна 3/5 высоты трапеции.
3) Находим искомую площадь:
а
3а
SMONP=SΔAOD – SΔAMP – SΔPND.
Слайд 10
По условию BC = 3a, АD = a, аh =
120.
1) ΔBOC∞ΔAOD ,
по трем углам
h
2) ΔBMC∞ΔAMP , по трем
углам,Тогда высота треугольника АМР равна 1/7 высоты трапеции.
3) Находим искомую площадь:
Ответ: 27 или 5.
3а
а
SMONP=SΔAOD – SΔAMP – SΔPND.
Слайд 11№4
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят
сторону ВС точками M и N, так что BM:MN=1:7. Найдите
ВС.Решение.
Пусть О – точка пересечения биссектрис.
Возможны два случая.
1) точка О – лежит внутри параллелограмма;
Рассмотрим первый случай.
2) точка О – лежит вне параллелограмма.
12
Слайд 12
№4
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят
сторону ВС точками M и N, так что BM:MN=1:7. Найдите
ВС.Решение.
М
N
Пусть О – точка пересечения биссектрис.
Рассмотрим первый случай.
12
1) ΔABN – равнобедренный, т.к.
∠ВNА=∠NAD- накрест лежащие;
значит ∠ВNА=∠ ВAN и AB=BN=12,
АN – биссектриса ∠А,
тогда
Найдем MN=BN-BM=12-1,5=10,5.
2) Аналогично, ΔDMC – равнобедренный, MC=DC=12.
Тогда NC= MC-MN=12-10,5=1,5.
3) Значит, ВС=ВМ+MN+NC=13,5.
1,5
10,5
1,5
Слайд 13
№4
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят
сторону ВС точками M и N, так что BM:MN=1:7. Найдите
ВС.Решение.
Рассмотрим второй случай:
точка О – лежит вне параллелограмма.
1)ΔABМ– равнобедренный, т.к.
Тогда АВ=ВМ=12.
2) Аналогично ΔDNC– равнобедренный,
3) Значит, ВС=ВN+NC=96+12=108.
12
12
12
12
∠ВMА=∠MAD- накрест лежащие;
значит ∠ВMА=∠ ВAM.
АМ – биссектриса ∠А,
Ответ: 13,5 или 108.
тогда NC=DC=12.
Слайд 14http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D1%8B
Использованные ресурсы
Тексты задач взяты с сайта Александра Ларина
http://alexlarin.narod.ru/ege.html
Рисунок
на слайде №2
Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg
и шаблон с сайта http://aida.ucoz.ru