Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координатно-векторный метод решения стереометрических задач
Содержание
- 1. Координатно-векторный метод решения стереометрических задач
- 2. 1. Координаты точки , 2. Координаты
- 3. Через любые две точки проходит прямая и
- 4. MNPЧерез любые три точки проходит плоскость и
- 5. Плоскость
- 6. I. Углы1. Угол межу прямыми - 2.
- 7. Введение системы координат
- 8. Обозначим АВ = а, AD = b,
- 9. Введение системы координат3. Правильная треугольная призмаВводим систему
- 10. Теперь рассмотрим всю призму вместе с построенной системой координат рис.2:Получаем следующие координаты точек:3. Правильная треугольная призмаВведение системы координат
- 11. Введение системы координат4. Правильная шестиугольная призмаВведем систему координат как показано на рис.Пусть все ребра равны 1.
- 12. Введение системы координат5. Правильная четырехугольная пирамидаОбозначим ее SABCD, где S —
- 13. II. Расстояния1. Расстояние от точки до прямой
- 14. 2. Расстояние от точки до плоскостивычисляется по формуле:II. Расстояния
- 15. B1
- 16. Получаем Делаем замену Получаем E(0;
- 17. Скачать презентанцию
Слайды и текст этой презентации
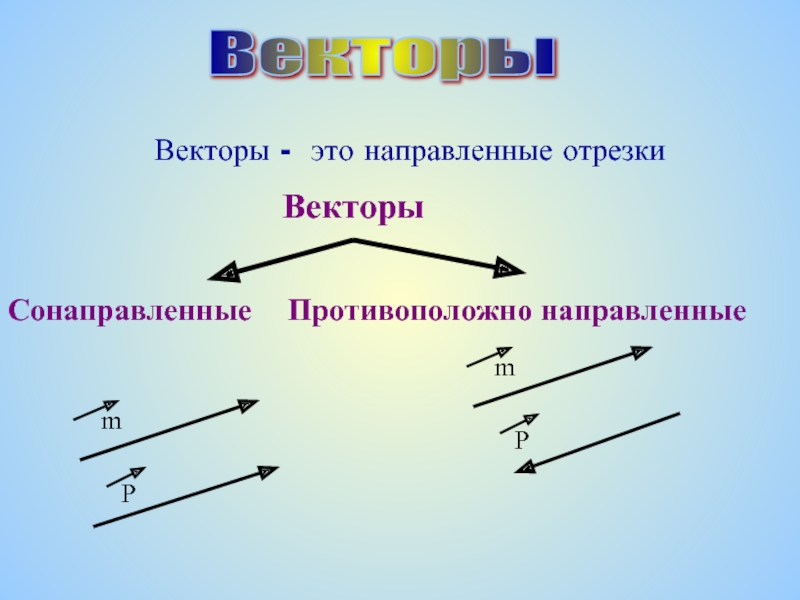
Слайд 21. Координаты точки
,
2. Координаты вектора
3. Длина
вектора
4. Скалярное произведение векторов
где α – угол
между векторами5. Скалярное произведение в координатах
6. Угол между векторами
Т.о. зная координаты точек можно найти координаты векторов и пользуясь формулой (п.6) косинус угла между этими векторами.
Векторы и угол между ними
Слайд 3Через любые две точки проходит прямая и притом только одна.
N
- направляющий вектор прямой MN.
Уравнение прямой MN:
Прямая
M
Слайд 4M
N
P
Через любые три точки проходит плоскость и притом только одна.
– вектор нормали плоскости
– это вектор
перпендикулярный этой плоскости
и
Уравнение плоскости:
где A, B, C – координаты вектора нормали плоскости, т.е.
* Если плоскость проходит через начало координат,
то D = 0, если нет, то D = 1.
Чтобы найти координаты вектора нормали (составить уравнение плоскости(MNP)) надо подставить координаты точек M, N, и P и решить систему из трех уравнений с
тремя неизвестными A, B, C.
Плоскость
Слайд 6I. Углы
1. Угол межу прямыми -
2. Угол межу плоскостями
-
3. Угол межу прямой и плоскостью -
это угол
между их направляющими векторамиэто угол между их нормалями
это угол равный разности 90°−угол между их
направляющим вектором и нормалью
Слайд 7Введение системы координат
В задачах типа C2 никаких координат и векторов нет.
Поэтому их придется вводить самостоятельно. Заметим, что координаты точек верхней плоскости отличаются от соответствующих координат точек нижней плоскости только
координатой z.
Стандартное введение системы координат для куба показано на рис.
Теперь у каждой вершины куба есть координаты.
Выпишем их:
А(0; 0; 0) В(1; 0; 0) С(1; 1; 0) D(0; 1; 0)
А1(0; 0; 1) В1(1; 0; 1) С1(1; 1; 1) D1(0; 1; 1)
1. Куб
Слайд 8Обозначим АВ = а, AD = b, АА1 = с.
Выпишем
координаты точек:
А(0; 0; 0) В(а; 0; 0)
С(a; b; 0) D(0; b; 0)А1(0; 0; c) В1(a; 0; c) С1(a; b; c) D1(0; b; c)
2. Прямоугольный параллелепипед
Введение системы координат
Слайд 9Введение системы координат
3. Правильная треугольная призма
Вводим систему координат:
Начало координат — в точке A;
Сторону
призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
Ось x направляем
по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.ГЛАВНОЕ учесть, что ось y НЕ совпадает с ребром AC, т.к. треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому вид сверху будет выглядеть так: рис.1.
Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому
AH = 1 · cos A = cos 60°;
CH = 1 · sin A = sin 60°.
Это надо для вычисления координат точки С.
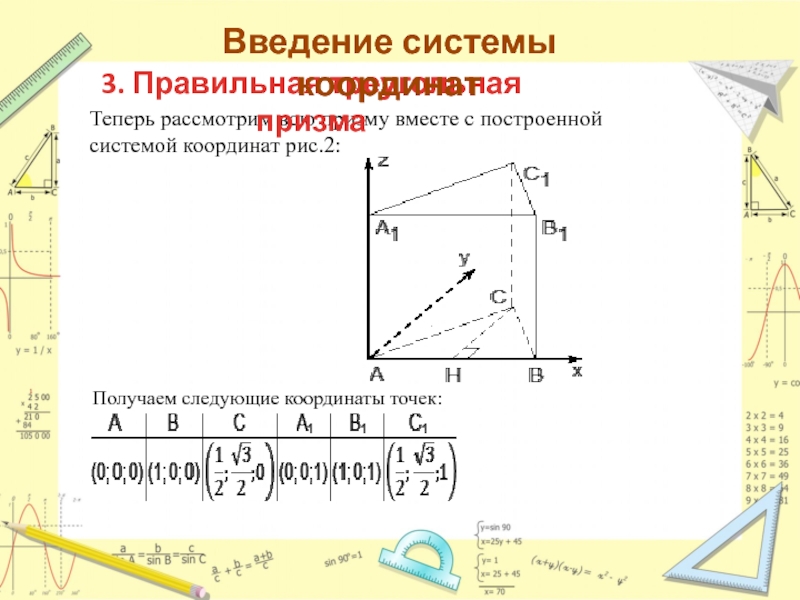
Слайд 10Теперь рассмотрим всю призму вместе с построенной системой координат рис.2:
Получаем следующие координаты
точек:
3. Правильная треугольная призма
Введение системы координат
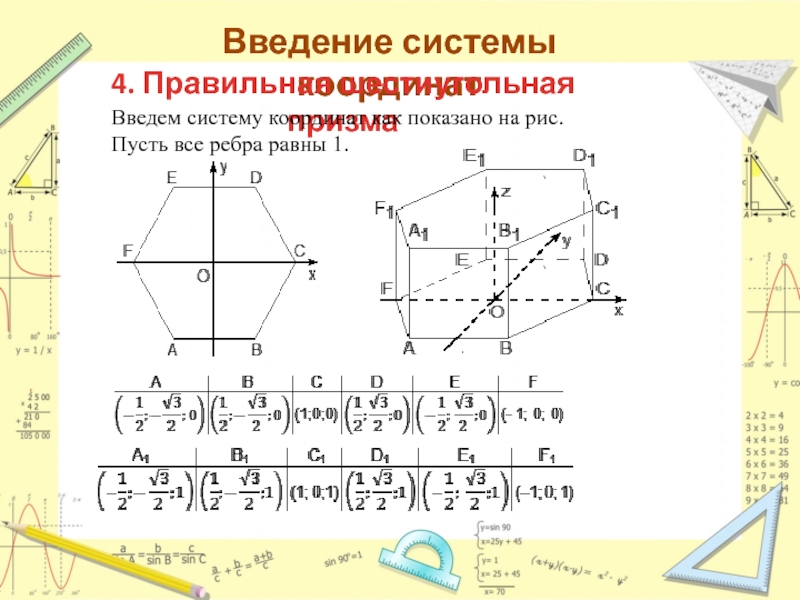
Слайд 11Введение системы координат
4. Правильная шестиугольная призма
Введем систему координат как показано
на рис.
Пусть все ребра равны 1.
Слайд 12Введение системы координат
5. Правильная четырехугольная пирамида
Обозначим ее SABCD, где S — вершина. Введем систему
координат.
Рассмотрим плоскость OXY.
В основании лежит квадрат, его
координаты известны.
Найдем
координаты точки S. Т.к. SH — высота к плоскости OXY,
точки S и H отличаются лишь координатой z.
Длина отрезка SH — это и есть координата z
для точки S, координаты точки H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам
(AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно,
SH = BH. Но BH — половина диагонали квадрата ABCD,
т.е. BH = AB · sin 45°. Т.о. получаем координаты всех точек:
Слайд 13II. Расстояния
1. Расстояние от точки до прямой
M
S
В
А
находим cosα
( * Если он «-», то находим cos β )
из
прямоугольного ΔMBS ( * или ΔMАS ) находим MS
MS − ?
Слайд 15B1
C1
А
DII. Расстояния
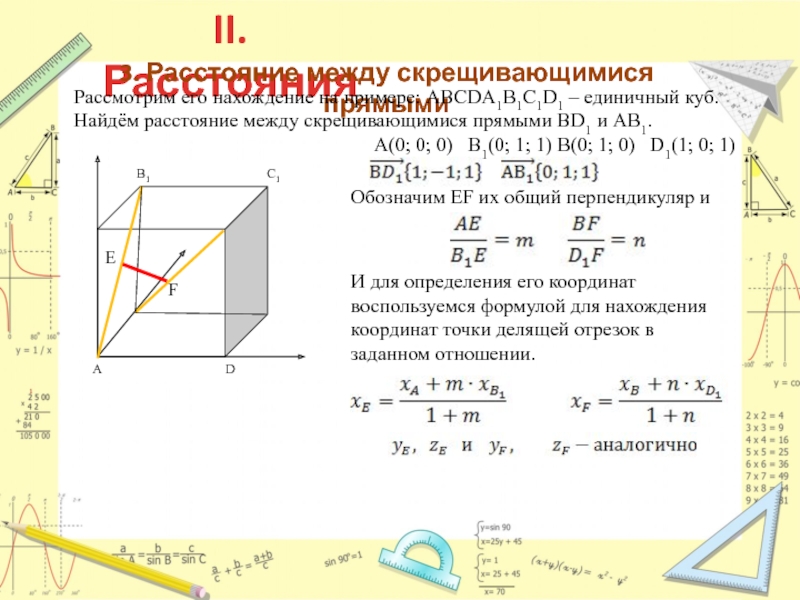
3. Расстояние между скрещивающимися прямыми
Рассмотрим его нахождение на примере: ABCDA1B1C1D1 – единичный куб. Найдём расстояние между скрещивающимися прямыми BD1 и AB1.
И для определения его координат воспользуемся формулой для нахождения координат точки делящей отрезок в заданном отношении.
E
F
A(0; 0; 0) В1(0; 1; 1) В(0; 1; 0) D1(1; 0; 1)
Обозначим EF их общий перпендикуляр и
Слайд 16Получаем
Делаем замену
Получаем E(0; p; p)
F(q; 1-q; q)
Т.к.
и
то их скалярное произведение
равно нулю.Решив систему
получаем
Следовательно
.
(Продолжение) Расстояние между скрещивающимися прямыми