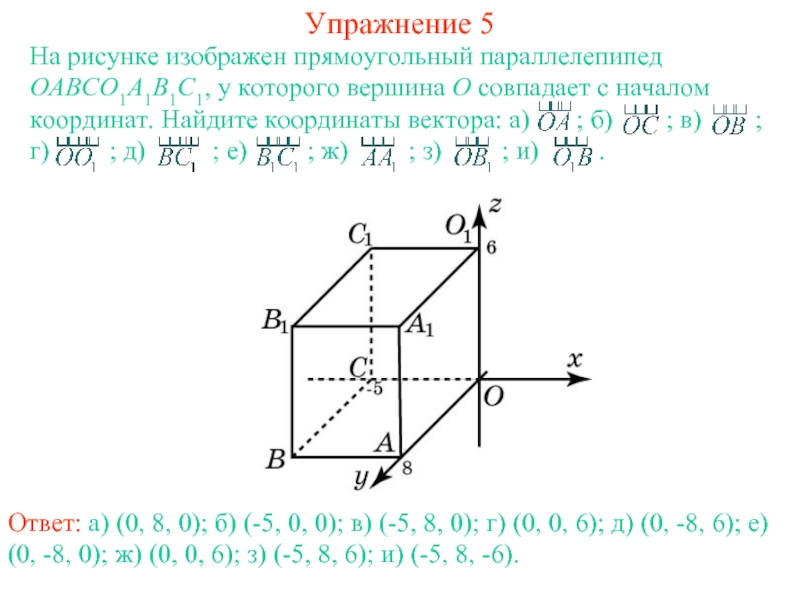
координат. Тогда координаты его конца называются координатами вектора. Обозначим
, , векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.