Математика в жизни

увидеть.
Почему геометрию часто называют холодной и сухой? Одна из

причин лежит в ее неспособности описать форму облаков, гор или деревьев. Облака - это не сферы, горы - не углы, линия побережья - не окружность, кора не гладкая, а молния не прямая линия…

но и несравненную
красоту.

Бертран Рассел

помощью простой
рекурсивной (повторяющейся)
процедуры превратил линию
в набор несвязанных

точек
(так называемая Пыль Кантора).
Он брал линию и удалял
центральную треть
и после этого повторял то же
самое с оставшимися отрезками.

Сantor Georg

алгоритм.
На первом шаге он брал прямую линию
и заменял ее

на 9 отрезков длиной
в 3 раза меньшей, чем длина исходной линии
(Часть 1 и 2 рисунка 1).
Далее он делал то же самое с
каждым отрезком получившейся
линии. И так до бесконечности.

Peano

странных объектах, без
какой либо попытки их систематизировать.
Так было,

пока за них не взялся Бенуа
Мандельброт – отец современной
фрактальной геометрии и слова
фрактал. Работая в IBM математическим
аналитиком, он изучал шумы в
электронных схемах, которые невозможно
было описать с помощью статистики.
Постепенно сопоставив факты, он
пришел к открытию нового направления
в математике –
фрактальной геометрии.

Benoît
Mandelbrot

геометрии. В 1993 году он стал лауреатом премии Вольфа по

физике. Бенуа Мандельброт был рожден в 1924 году в Варшаве. В 1936 году его семья уезжает в Париж, где юный Бенуа попадает под влияние своего дяди Шолема Мандельбройта, бывшего известным математиком, входящим в группу математиков с общим псевдонимом «Николя Бурбаки».

геометрическая фигура,
состоящая из частей и которая
может быть поделена

на части,
каждая из которых будет представлять
уменьшенную копию целого
(по крайней мере, приблизительно)

классическим пример - "Какова длина берега Британии?"

первый - снежинка Коха. Строится она на основе равностороннего треугольника.

Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длина кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длины. Получается, что наша бесконечная кривая покрывает ограниченную площадь

эту же процедуру для трех образовавшихся треугольников (за исключением центрального)

и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.

на основе алгебраических формул иногда весьма простых.
Методов получения алгебраических

фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:
С течением времени стремится к бесконечности.
Стремится к 0
Принимает несколько фиксированных значений и не выходит за их пределы.
Поведение хаотично, без каких либо тенденций.

- это число, состоящее из двух частей - действительной и

мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а вот мнимая часть bi интересней, i - называют мнимой единицей. Почему мнимой? А потому, что если мы возведем i в квадрат, то получим -1.
Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень, нельзя только их сравнивать. Комплексное число можно изобразить как точку на плоскости, у которой координата Х- это действительная часть a, а Y- это коэффициент при мнимой части b.
Функционально множество Мандельброта определяется как Zn+1=Zn*Zn+C.

Справа - небольшой участок множества Мандельброта, увеличенное до размеров предыдущего

рисунка.

Майкла Барнсли из технологического института штата Джорджия. Он пытался кодировать

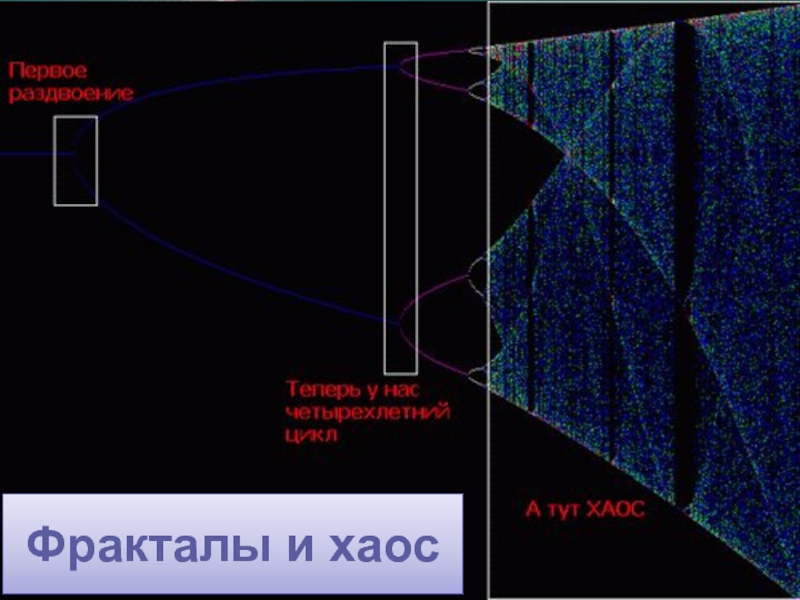
изображения с помощью фракталов.

отсутствие предсказуемости. Хаос возникает в динамических системах, когда для двух

очень близких начальных значений система ведет себя совершенно по-разному.

Фракталы и хаос

процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя,

облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Радиотехника
Фрактальные антенны
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.
фракталов (программа).

о том, что вместо самого изображения можно хранить сжимающее отображение,

для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.
Компьютерная графика
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений(Генератор фракталов (программа)).
Децентрализованные сети
Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
Экономика и финансы
А. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс.

рождение новых представлений неизбежно сложного и красивого мира.