Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объёмы и поверхности тел вращения
Содержание
- 1. Объёмы и поверхности тел вращения
- 2. Тела вращения
- 3. оглавление1.Виды тел вращения 2.Определения тел вращения: а)цилиндр б)конус в)шар3.Сечения тел вращения: а)цилиндр б)конус в)шар4.Объёмы тел вращения 5.Площади поверхностей тел вращенияЗавершить работу
- 4. ВИДЫ ТЕЛ ВРАЩЕНИЯЦилиндр-тело, которое описывает прямоугольник при
- 5. ОПРЕДЕЛЕНИЕ ЦИЛИНДРАЦилиндром называется тело, которое состоит из
- 6. ОПРЕДЕЛЕНИЕ КОНУСАКонусом называется тело,которое состоит из круга-основания
- 7. СЕЧЕНИЯ ЦИЛИНДРАСечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник.Осевое
- 8. ОПРЕДЕЛЕНИЕ ШАРАШаром называется тело, которое состоит из
- 9. СЕЧЕНИЕ КОНУСАСечение конуса плоскостью,проходящей через его вершину,
- 10. СЕЧЕНИЯ ШАРАСечение шара плоскостью есть круг. Центр
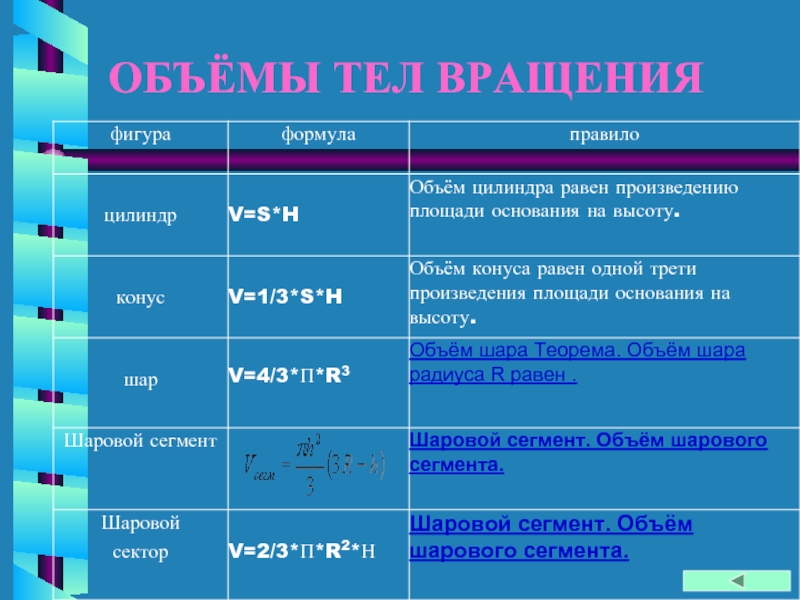
- 11. ОБЪЁМЫ ТЕЛ ВРАЩЕНИЯ
- 12. ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ
- 13. Объём шара Теорема. Объём шара радиуса R
- 14. Шаровой сегмент. Объём
- 15. Шаровой сектор . Объём шарового сектора.Шаровой сектор, тело, которое получается из шарового сегмента и конуса.Объём сектораV=2/3ПR2H
- 16. Задача № 1. Цистерна имеет форму цилиндра
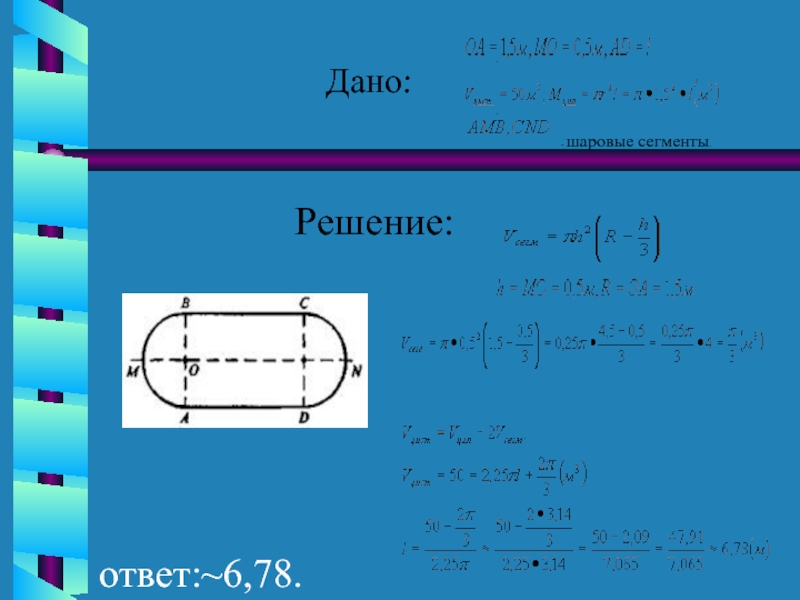
- 17. Дано: . . - шаровые сегменты.
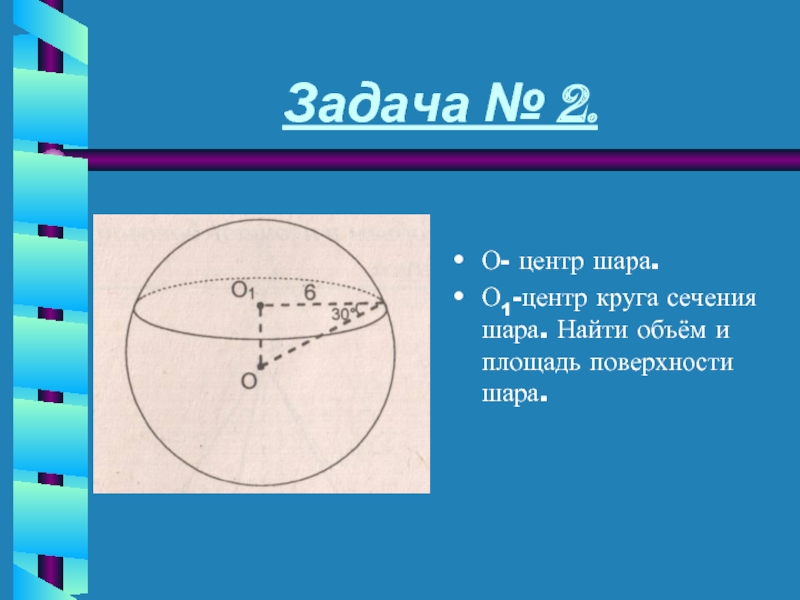
- 18. Задача № 2.О- центр шара. О1-центр круга сечения шара. Найти объём и площадь поверхности шара.
- 19. Дано: шар
- 20. Задача № 3 Полуцилиндрический свод подвала
- 21. Дано: Цилиндр.АВСД-осевое сечение.
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3оглавление
1.Виды тел вращения
2.Определения тел вращения:
а)цилиндр
б)конус
в)шар
3.Сечения тел вращения:
а)цилиндр
б)конус
в)шар
4.Объёмы тел вращения
5.Площади поверхностей
тел вращения
Завершить работу
Слайд 4ВИДЫ ТЕЛ ВРАЩЕНИЯ
Цилиндр-тело, которое описывает прямоугольник при вращении его около
стороны как оси
Конус-тело, которое получено при вращении прямоугольного треугольника вокруг
его катета как осиШар-тело полученное при вращении полукруга вокруг его диаметра как оси
Слайд 5ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Цилиндром называется тело, которое состоит из двух кругов, не
лежащих в одной плоскости и совмещаемых параллельным переносом, и всех
отрезков, соединяющих соответствующие точки этих кругов.Круги называются основаниями цилиндра, а отрезки,соединяющие соответствующие точки окружностей кругов,образующими цилиндра.
Слайд 6ОПРЕДЕЛЕНИЕ КОНУСА
Конусом называется тело,которое состоит из круга-основания конуса,точки, не лежащей
в плоскости этого круга,вершины конуса и всех отрезков,соединяющих вершину конуса
с точками основания.
Слайд 7СЕЧЕНИЯ ЦИЛИНДРА
Сечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник.
Осевое сечение-сечение цилиндра плоскостью,проходящей
через его ось
Сечение цилиндра плоскостью, параллельной основаниям, представляет собой круг.
Слайд 8ОПРЕДЕЛЕНИЕ ШАРА
Шаром называется тело, которое состоит из всех точек пространства,
находящихся на расстоянии,не большем данного, от данной точки. Эта точка
называется центром шара, а данное расстояние радиусом шара.
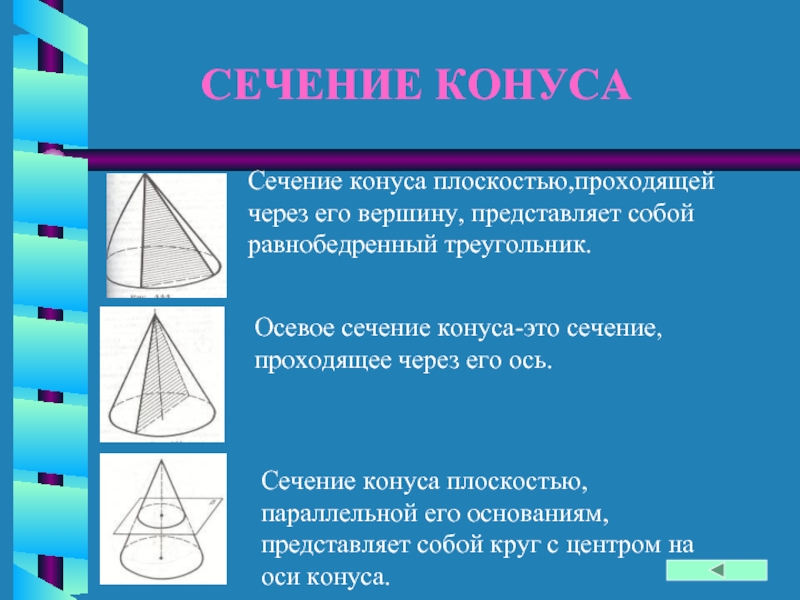
Слайд 9СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью,проходящей через его вершину, представляет собой равнобедренный
треугольник.
Осевое сечение конуса-это сечение, проходящее через его ось.
Сечение конуса плоскостью,
параллельной его основаниям, представляет собой круг с центром на оси конуса.
Слайд 10СЕЧЕНИЯ ШАРА
Сечение шара плоскостью есть круг. Центр этого шара есть
основание перпендикуляра,опущенного из центра шара на секущую плоскость.
Сечение шара диаметральной
плоскостью называется большим кругом.
Слайд 13Объём шара
Теорема. Объём шара радиуса R равен .
Доказательство. Рассмотрим шар
радиуса R с центром в точке О и выберем ось
Ох произвольным образом (рис. ). Сечение шара плоскостью, перпендикулярной к оси Ох и проходящей через точку М этой оси, является кругом с центром в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим:(2.6.1)
Так как , то (2.6.2)
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х,удовлетворяющих условию . Применяя основную формулу для вычисления объемов тел при
, получим
Теорема доказана.
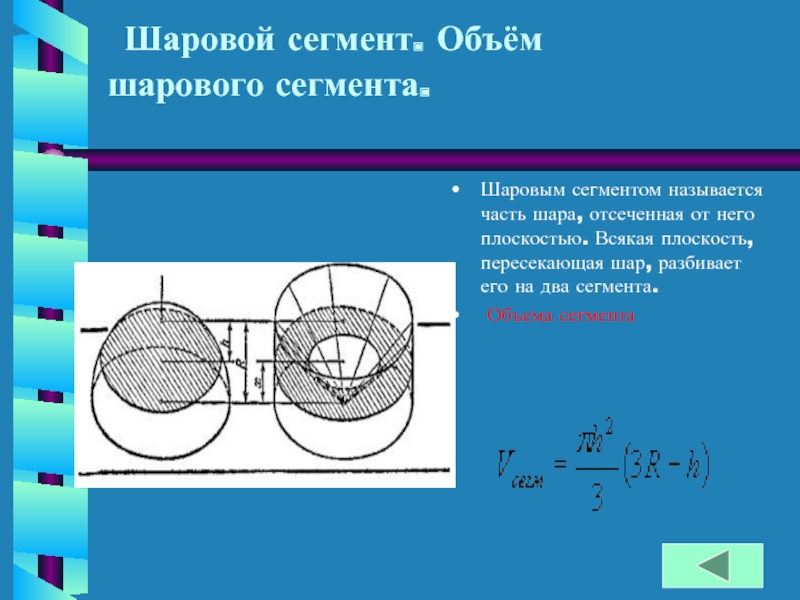
Слайд 14 Шаровой сегмент. Объём шарового сегмента.
Шаровым
сегментом называется часть шара, отсеченная от него плоскостью. Всякая плоскость,
пересекающая шар, разбивает его на два сегмента.Объема сегмента
Слайд 15Шаровой сектор . Объём шарового сектора.
Шаровой сектор, тело, которое получается
из шарового сегмента и конуса.
Объём сектора
V=2/3ПR2H
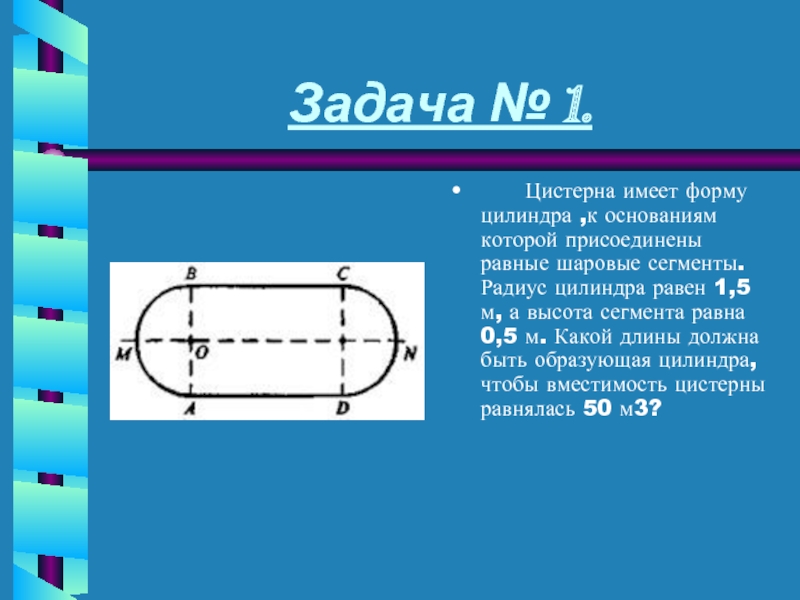
Слайд 16Задача № 1.
Цистерна имеет форму цилиндра ,к основаниям которой
присоединены равные шаровые сегменты. Радиус цилиндра равен 1,5 м, а
высота сегмента равна 0,5 м. Какой длины должна быть образующая цилиндра, чтобы вместимость цистерны равнялась 50 м3?Слайд 18Задача № 2.
О- центр шара.
О1-центр круга сечения шара. Найти
объём и площадь поверхности шара.
Слайд 19Дано: шар сечение
с центром О1.Rсеч.=6см. Угол
ОАВ=300.Vшара=? Sсферы=?Решение:
V=4/3ПR2 S=4ПR2
В ∆ ОО1А:угол О1=900,О1А=6,
угол ОАВ=300.tg300=ОО1/О1А ОО1=О1А*tg300.ОО1=6*√3÷3=2√3
ОА=R=OO1(по св-ву катета леж.против угла 300).
ОА=2√3÷2=√3
V=4П(√3)2÷3=(4*3,14*3)÷3=12,56
S=4П(√3)2=4*3,14*3=37,68
Ответ:V=12,56; S=37,68.
Слайд 20Задача № 3
Полуцилиндрический свод подвала имеет 6м. длины
и 5,8м. в диаметре.Найдите полную поверхность подвала.
Слайд 21Дано: Цилиндр.АВСД-осевое сечение.
АД=6м. D=5,8м.
Sп.под.=?Решение :
Sп.под.=(Sп÷2)+SАВСД
Sп÷2=(2ПRh+2ПR2)÷2=2(ПRh+ПR2)÷2=ПRh+ПR2
R=d÷2=5,8÷2=2,9 м.
Sп÷2=3,14*2,9+3,14*(2,9)2=
54,636+26,4074=81,0434
АВСД-прямоуг.(по опр.осев.сеч.)
SАВСД=АВ*АД=5,8*6=34,8м2
Sп.под.=34,8+81,0434≈116м2.
Ответ:Sп.под.≈116м2.