Открытый урок "Тригонометрические формулы" 10 класс

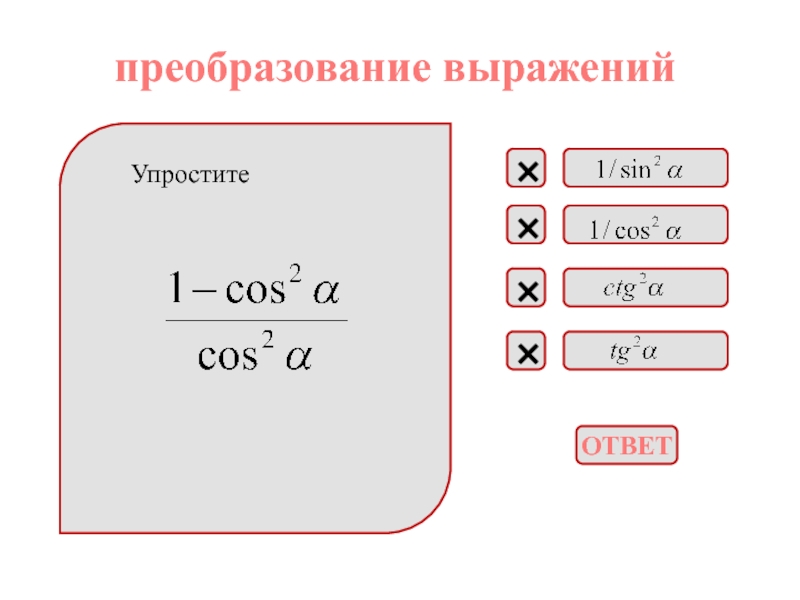
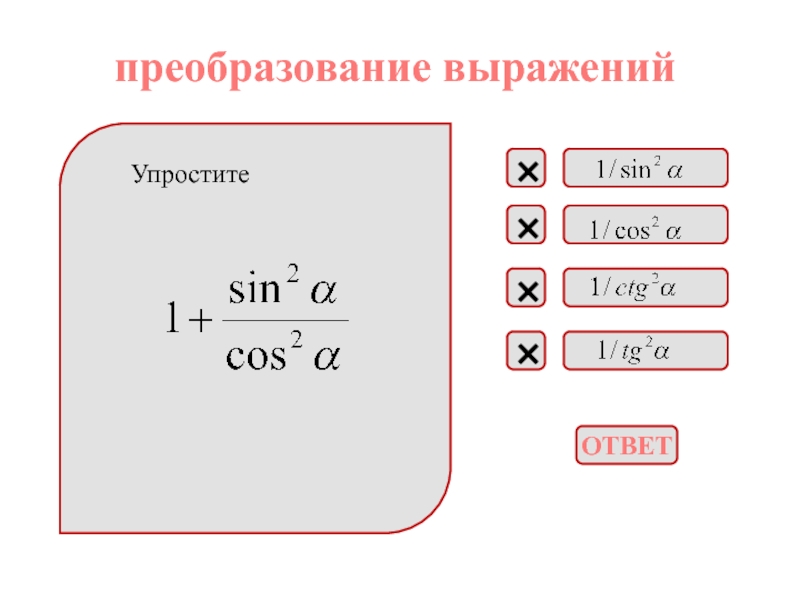
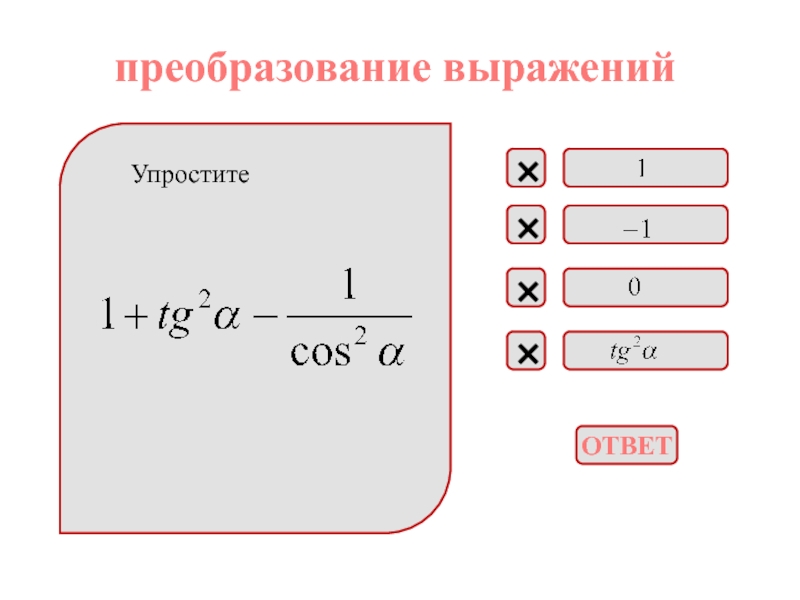
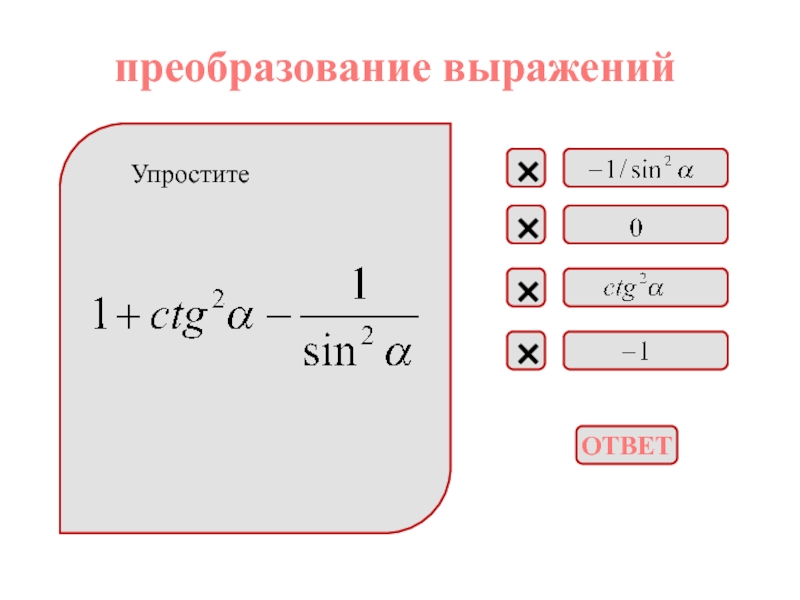
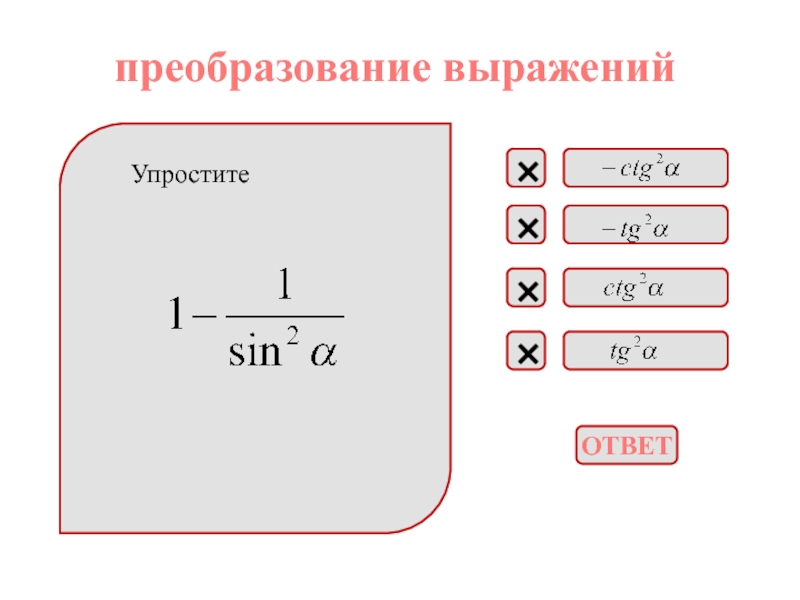
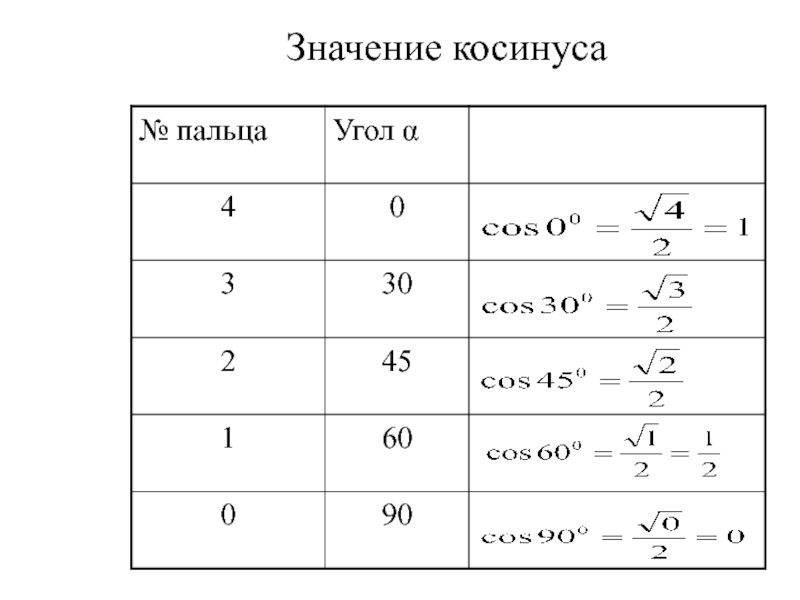
приведения, формулы двойного угла, формулы сложения;
Повторить основное тригонометрическое тождество и

интересно
Итог урока
Домашнее задание

вокруг начала координат на угол α

tg α =

sin2 α +cos2

Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
tg α =

sin2 α +cos2 α=

1+ tg2 α=

sin(-α)=
tg (-α) =
cos (α+β)=
sin (α-β)=
sin 2α=

tg (α+β)=

sin(π- α)=

cos ( + α)=

начала координат на угол α
ctg α=
tg α∙ ctg α=

1+

Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α

сtg α=
tg α∙ ctg α = 1

1+ ctg2 α=

cos (-α) = cos α
ctg (-α) = -ctg α
cos (α-β)=cosα cosβ +sinα sinβ
sin (α+β)= sinα cosβ + cosα sinβ
cos 2α=cos2 α-sin2 α

tg 2α=
cos(π- α)= - cos α

sin ( + α)=-cos α

ОТВЕТ:

3,25.
2) Дано:

Найдите значение:

а) б) в)

вариант 2
1) Найдите значение

а) -3,5; б) 9,5; в) -0,5; г) 6,5.

2) Дано:

Найдите значение:

а) б) в) г)

3) Упростите выражение:



а) б) в) г)

происхождения, обозначающее «измерение треугольников».
Гиппарх является автором первых тригонометрических таблиц

Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры.

, k=1, a=1
Детская школа Гауди в Барселоне
В архитектуре

или синуса (гармоническому закону), называются гармоническими колебаниями.
Выражение, стоящее под

Тригонометрия в физике

среды
α-угол падения, β-угол преломления света

Теория радуги


sin β
sin α
n1
n2
=
Северное

ладони

а),б)

Доказать: