Перпендикуляр и наклонная 10 класс

Содержание

1. Перпендикуляр и наклонная 10 класс
2. Теорема о перпендикуляре и наклоннойТеорема. Перпендикуляр, опущенный
3. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮУглом между наклонной
4. Теорема о трех перпендикулярахТеорема. Если прямая, лежащая
5. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ И ПЛОСКОСТИРасстоянием
6. Верно ли утверждение: «Если из одной точки,
7. К плоскости прямоугольника ABCD в точке пересечения
8. Основание ABCD пирамиды SABCD – прямоугольник, AB
9. Из точки A к данной плоскости проведены
10. Из точки A к данной плоскости проведены
11. Из точки A к данной плоскости проведены
12. Отрезки двух наклонных, проведенных из одной точки
13. Найдите диагональ прямоугольного параллелепипеда, ребра которого равны a, b, c.Упражнение 5
14. Упражнение 6В кубе найдите угол между: а)
15. Упражнение 4 (Пример 2. с. 362)В правильном
16. Отрезок BC длиной 12 см является проекцией
17. Упражнение 8В правильной треугольной пирамиде сторона основания
18. Упражнение 9Через сторону квадрата проведена плоскость, составляющая
19. Дан прямоугольный треугольник ABC, катеты которого AC
20. Сторона ромба равна a, острый угол 60°.
21. Скачать презентанцию

Теорема о перпендикуляре и наклоннойТеорема. Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости.Доказательство. Пусть AB – наклонная к плоскости α, AO

Главная
Геометрия
Перпендикуляр и наклонная 10 класс

Слайды и текст этой презентации

Слайд 1ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Пусть точка A не принадлежит плоскости π. Проведем

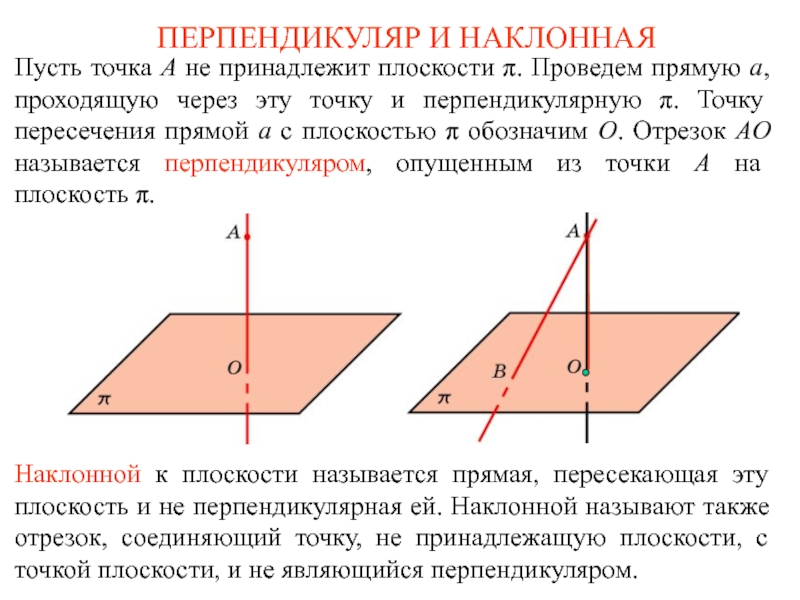
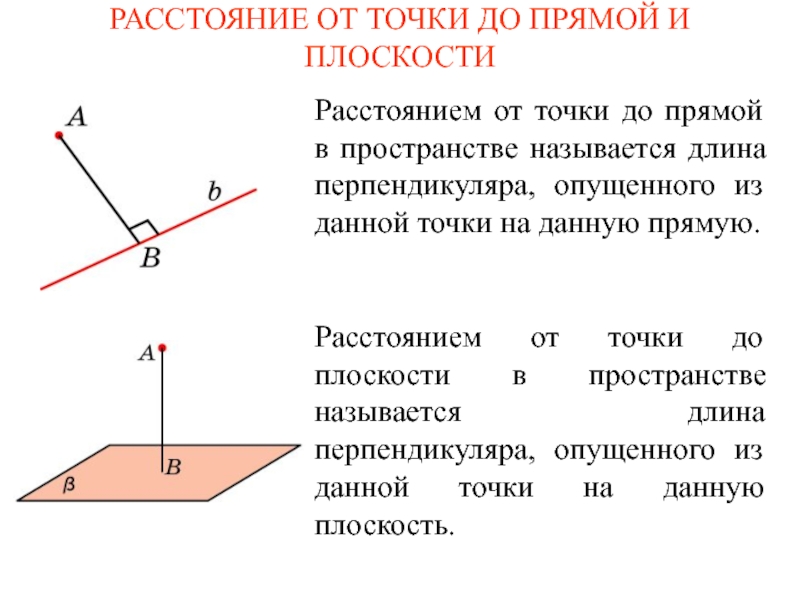
прямую a, проходящую через эту точку и перпендикулярную π. Точку

пересечения прямой a с плоскостью π обозначим O. Отрезок AO называется перпендикуляром, опущенным из точки A на плоскость π.

Наклонной к плоскости называется прямая, пересекающая эту плоскость и не перпендикулярная ей. Наклонной называют также отрезок, соединяющий точку, не принадлежащую плоскости, с точкой плоскости, и не являющийся перпендикуляром.

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯПусть точка A не принадлежит плоскости π. Проведем прямую a, проходящую через эту точку и

Слайд 2Теорема о перпендикуляре и наклонной
Теорема. Перпендикуляр, опущенный из точки на

плоскость, короче всякой наклонной, проведенной из той же точки к

той же плоскости.

Доказательство. Пусть AB – наклонная к плоскости α, AO – перпендикуляр, опущенный на эту плоскость, OB-ортогональная проекция. Треугольник AOB прямоугольный, AB – гипотенуза, AO – катет. Следовательно, AO < AB.

Теорема о перпендикуляре и наклоннойТеорема. Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той

Слайд 3УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между наклонной и плоскостью называется

угол между этой наклонной и ее ортогональной проекцией на данную

плоскость.
Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮУглом между наклонной и плоскостью называется угол между этой наклонной и ее ортогональной

Слайд 4Теорема о трех перпендикулярах
Теорема. Если прямая, лежащая в плоскости, перпендикулярна

ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и

самой наклонной.

Доказательство. Т.к.АО - перпендикуляр к плоскости α, то АО перпендикулярна прямой а плоскости α. Прямая а плоскости α перпендикулярна проекции OB наклонной АВ. Тогда она будет перпендикулярна двум пересекающимся прямым OB и AO. По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости АOВ и, следовательно, она будет перпендикулярна наклонной АВ, принадлежащей этой плоскости.

Дано:

Д-ть: