Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильная треугольная пирамида
Содержание
- 1. Правильная треугольная пирамида
- 2. Треугольная пирамида—многогранник, основание которого —правильный треугольник , а
- 3. Элементы пирамиды апофема — высота боковой грани правильной
- 4. Пирамида называется правильной треугольной, если основанием её
- 5. Свойства правильной треугольной пирамиды Все диагонали пирамиды
- 6. Формулы, связанные с правильной треугольной пирамидой Объём
- 7. Для нахождения боковой поверхности в правильной треугольной
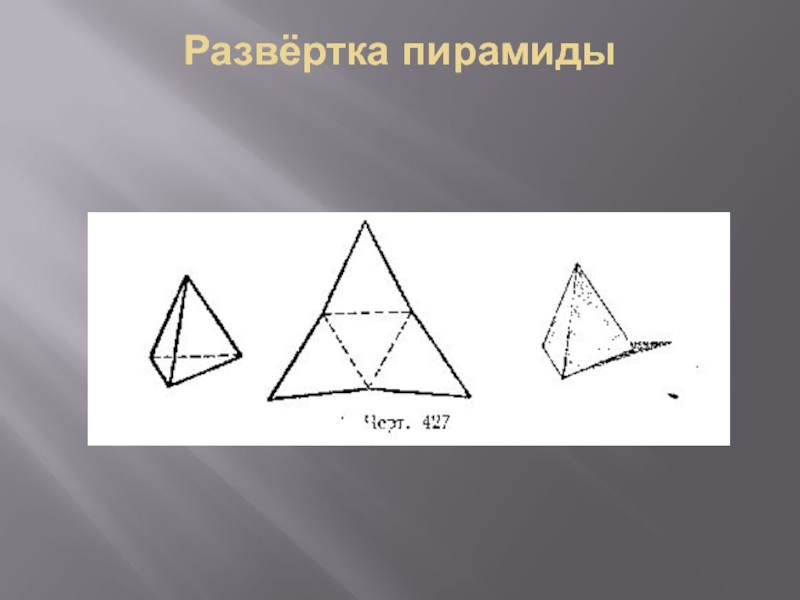
- 8. Развёртка пирамиды
- 9. Развёртка треугольной пирамиды При построении развёртки пирамиды
- 10. Алгоритм построения Определяют натуральную величину основания пирамиды
- 11. Теоремы, связывающие пирамиду с другими геометрическими телами
- 12. КонусКонус называется вписанным в пирамиду, если вершины
- 13. ЦилиндрЦилиндр называется вписанным в пирамиду, если вершина
- 14. Скачать презентанцию
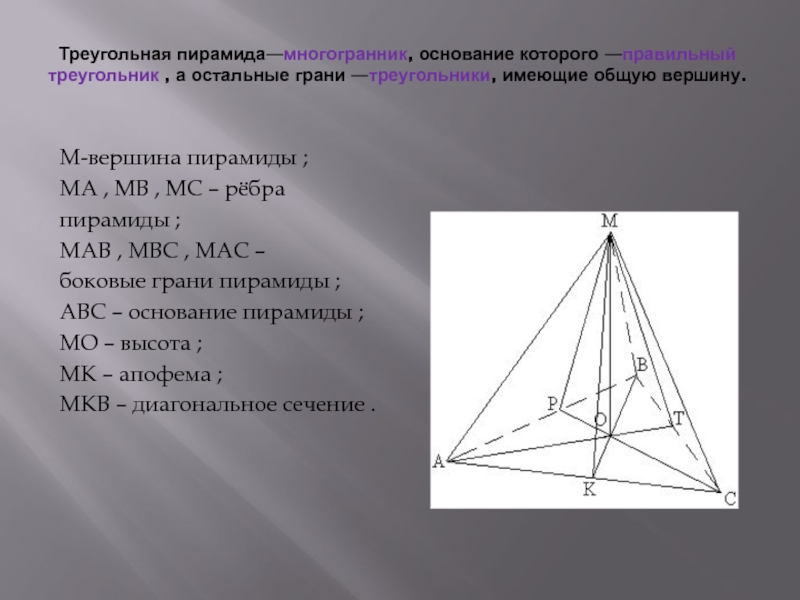
Треугольная пирамида—многогранник, основание которого —правильный треугольник , а остальные грани —треугольники, имеющие общую вершину. M-вершина пирамиды ;MA , MB , MC – рёбра пирамиды ;MAB , MBC , MAC – боковые грани
Слайды и текст этой презентации
Слайд 1Правильная Треугольная пирамида
Выполнила учитель МБОУ СОШ №67 Кожеурова Галина Владимировна
г.Воронеж
Слайд 2Треугольная пирамида—многогранник, основание которого —правильный треугольник , а остальные грани —треугольники, имеющие
общую вершину.
M-вершина пирамиды ;
MA , MB , MC –
рёбра пирамиды ;
MAB , MBC , MAC –
боковые грани пирамиды ;
ABC – основание пирамиды ;
MO – высота ;
MK – апофема ;
MKB – диагональное сечение .
Слайд 3Элементы пирамиды
апофема — высота боковой грани правильной пирамиды;
боковые грани — треугольники, сходящиеся
в вершине пирамиды;
боковые ребра — общие стороны боковых граней;
вершина пирамиды — точка,
соединяющая боковые рёбра и не лежащая в плоскости основания;высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
основание — многоугольник, которому не принадлежит вершина пирамиды.
осью правильной пирамиды называется прямая, содержащая её высоту.
Слайд 4Пирамида называется правильной треугольной, если
основанием её является правильный треугольник,
а вершина проецируется в центр основания. Тогда она обладает такими
свойствами:боковые ребра - равны;
все боковые грани — равные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания;
площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему.
Усеченная пирамида, которая получается из правильной, также называется правильной. Боковые грани правильной усеченной пирамиды- равные равнобокие трапеции; их высоты называются апофемами.
Слайд 5Свойства правильной треугольной пирамиды
Все диагонали пирамиды принадлежат её граням.
Если все
боковые ребра равны, то:
около основания пирамиды можно описать окружность, причём
вершина пирамиды проецируется в её центр;боковые ребра образуют с плоскостью основания равные углы.
Если боковые грани наклонены к плоскости основания под одним углом, то:
в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
высоты боковых граней равны;
площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.
Слайд 6Формулы, связанные с правильной треугольной пирамидой
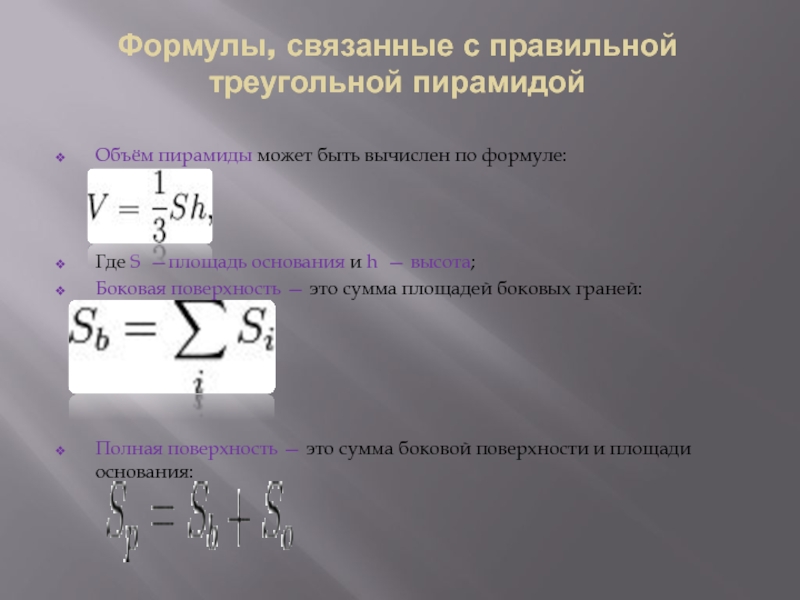
Объём пирамиды может быть вычислен
по формуле:
Где S —площадь основания и h — высота;
Боковая поверхность —
это сумма площадей боковых граней:Полная поверхность — это сумма боковой поверхности и площади основания:
Слайд 7Для нахождения боковой поверхности в правильной треугольной пирамиде можно использовать
формулы:
где а - апофема боковой грани, P —периметр основания, n — число
сторон основания ( для треугольной пирамиды – 3 ), b— боковое ребро, α — плоский угол при вершине пирамиды.Слайд 9Развёртка треугольной пирамиды
При построении развёртки пирамиды применяется способ треугольника. Развёртка
боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников
— граней пирамиды и правильного теугольника — основания. Поэтому построение развёртки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трём сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину рёбер и сторон основания. Определение истинной величины основания и рёбер пирамиды.Слайд 10Алгоритм построения
Определяют натуральную величину основания пирамиды (например методом замены плоскостей
проекций);
Определяют истинную величину всех рёбер пирамиды любым из известных способов
(в данном примере натуральная величина всех рёбер пирамиды определена методом вращения вокруг оси, перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды);Строят основание пирамиды и по найденным трём сторонам строят какую-либо из боковых граней, пристраивая к ней следующие.
Точки, расположенные внутри контура развёртки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех рёбер, по которым многогранник разрезан, на развёртке соответствуют две точки, принадлежащие контуру развёртки.
Слайд 11Теоремы, связывающие пирамиду с другими геометрическими телами
Сфера
около пирамиды можно описать
сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (необходимое
и достаточное условие).[Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Слайд 12Конус
Конус называется вписанным в пирамиду, если вершины их совпадают, а
его основание вписано в основание пирамиды. Причём вписать конус в
пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие);
Высоты у таких конусов и пирамид равны между собой.
Слайд 13Цилиндр
Цилиндр называется вписанным в пирамиду, если вершина пирамиды принадлежит его
одному основанию, а другое его основание совпадает с окружностью вписанной
в сечение пирамиды плоскостью, параллельной основанию. Причём вписать цилиндр в пирамиду можно только тогда, когда в основании пирамиды — описанный многоугольник (необходимое и достаточное условие);Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания цилиндра. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).