Геометрические задачи на экстремум

которых некоторая величина принимает наибольшее и наименьшее значение, принято называть

задачами «на экстремум» или задачами «на максимум и минимум».
Extremum (лат.)-крайний
Maximum (лат.)-наибольший
Minimum (лат.)-наименьший
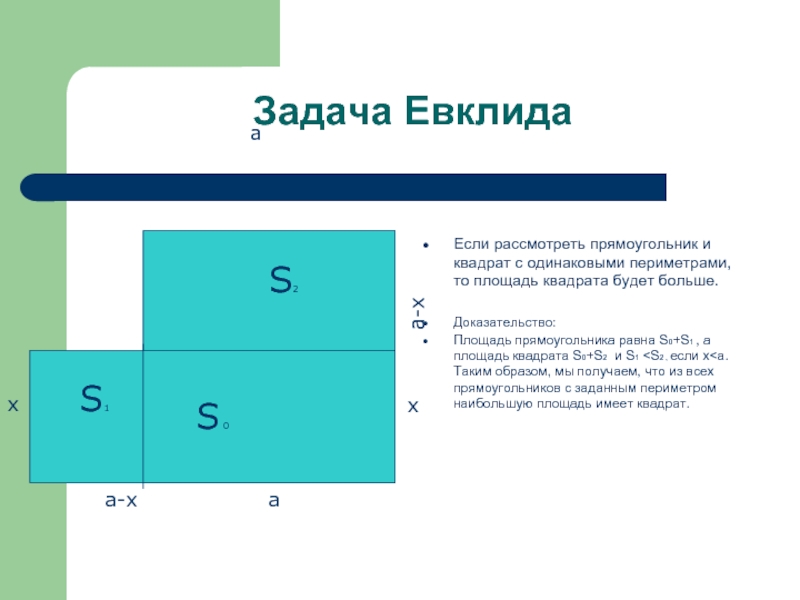
Задачи, в которых фигура с экстремальными свойствами отыскивается среди других с равными периметрами. Называются изопериметрическими или «задачами Дидоны».

площадь квадрата будет больше.

Доказательство:
Площадь прямоугольника равна S0+S1 , а площадь

квадрата S0+S2 и S1

S 0

а

а

а-х

х

а-х

х

S2

S1

Вынужденная бежать из своего города, Диона вместе со своими

спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Диона разрезала воловью шкуру на узкие ремешки и, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть воловьей одной шкурой .

и равным числом сторон наибольшую площадь имеет правильный многоугольник
Из двух

правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше

Из всех плоских фигур с равным периметром наибольшую площадь имеет круг.

ограничиваемый участок прямоугольной формы, то наибольшую площадь будет иметь прямоугольник

с длинами сторон р/4 и р/2.
Р-ПЕРИМЕТР УЧАСТКА.

море

берег

участок

р/4

Р/2

поверхности его объем был наибольшим?
Решение. Пусть а, b и с-

длины ребер. S-площадь полной поверхности, V- объем.
S=2(ab+bc+ac), V=abc. Применим неравенство: среднее арифметическое больше или равно среднему геометрическому Знак равенства достигается при a=b=c и при этом объем будет наибольшим. Итак, наибольший объем имеет куб.

ПРИМЕНЕНИЕ НЕРАВЕНСТВ