Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Призма Объем наклонной призмы
Содержание
- 1. Призма Объем наклонной призмы
- 2. ПРИЗМА.
- 3. Евклид определяет призму как телесную
- 4. Определение 1.Многогранник, две грани которого - одноименные
- 5. Свойства призмы. 1. Основания призмы являются
- 6. Все призмы делятся на прямые и наклонные.
- 7. Определение 2. Прямая призма, основанием которой
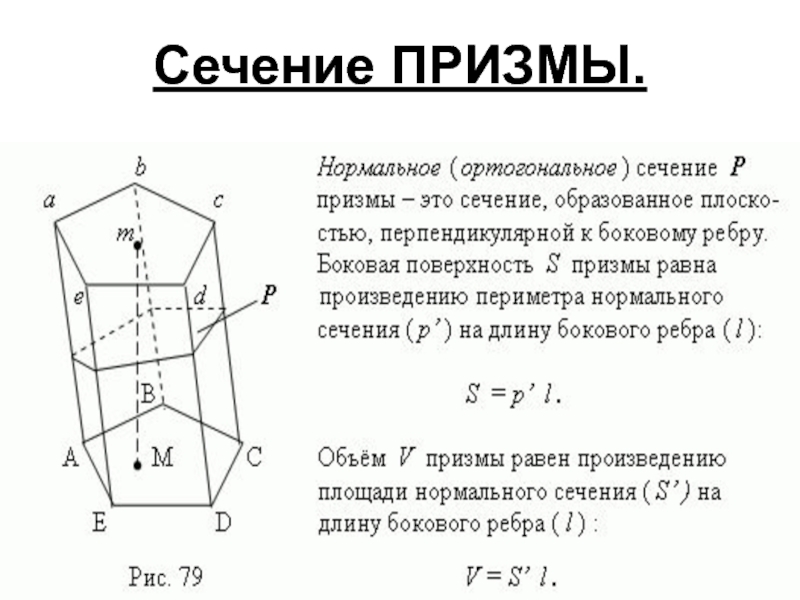
- 8. Сечение ПРИЗМЫ.
- 9. A1B1C1Расстояния между ребрами наклоннойтреугольной призмы равны: 2см,
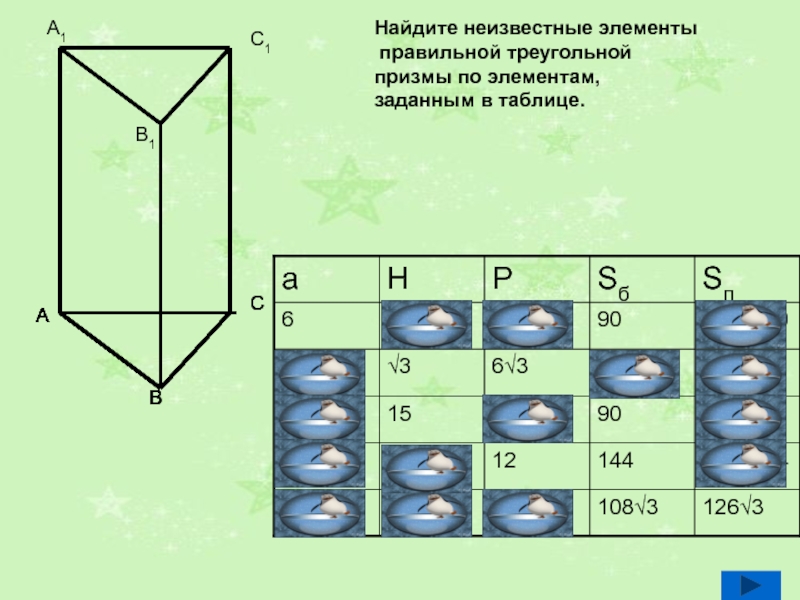
- 10. Найдите неизвестные элементы правильной треугольной призмы по элементам, заданным в таблице.ABCAABCABCABCABCABCABA
- 11. Слайд 11
- 12. Скачать презентанцию
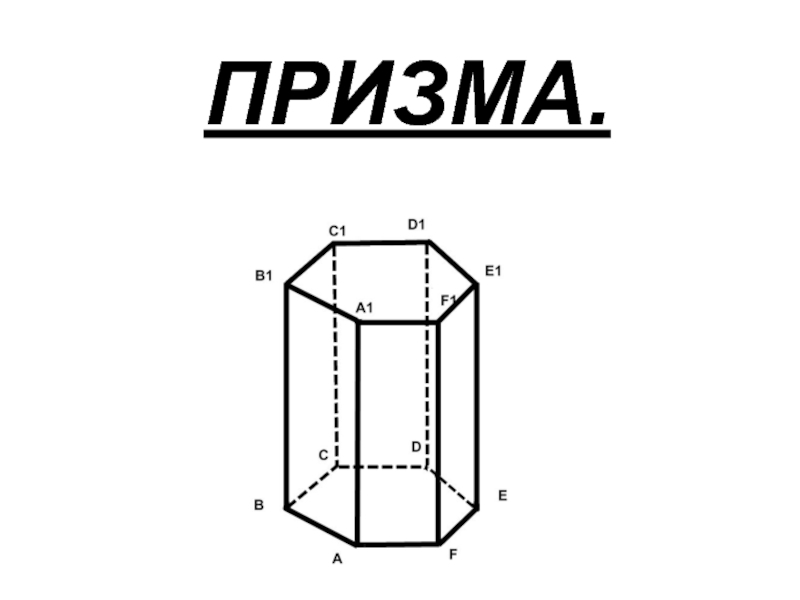
ПРИЗМА.
Слайды и текст этой презентации
Слайд 4Определение 1.
Многогранник, две грани которого - одноименные многоугольники, лежащие в
параллельных плоскостях, а любые два ребра, не лежащие в этих
плоскостях, параллельны, называется призмой.Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями. Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.
Слайд 5Свойства призмы.
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы
являются параллелограммами.
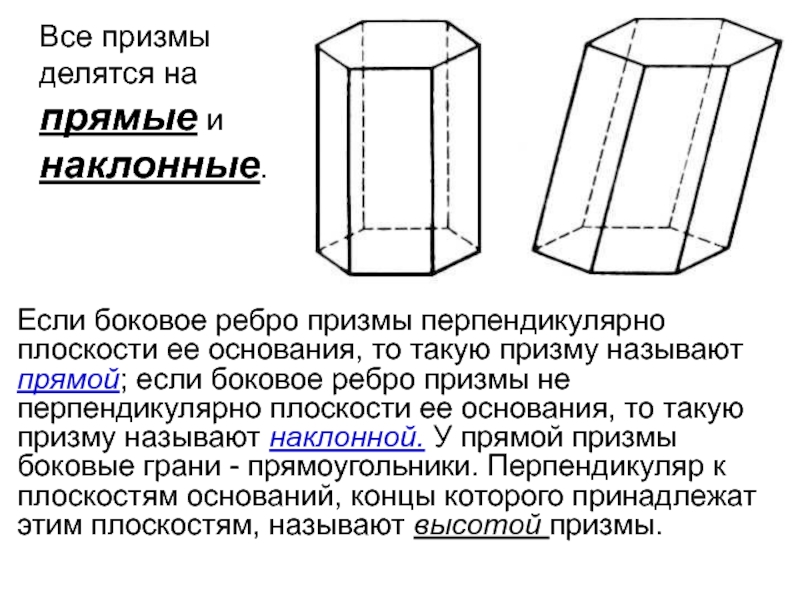
3. Боковые ребра призмы равны.Слайд 6Все призмы делятся на прямые и наклонные.
Если боковое ребро призмы
перпендикулярно плоскости ее основания, то такую призму называют прямой; если
боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.Слайд 7Определение 2.
Прямая призма, основанием которой служит правильный многоугольник,
называется правильной призмой.
Свойства правильной призмы :
1. Основания
правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны. Слайд 9A1
B1
C1
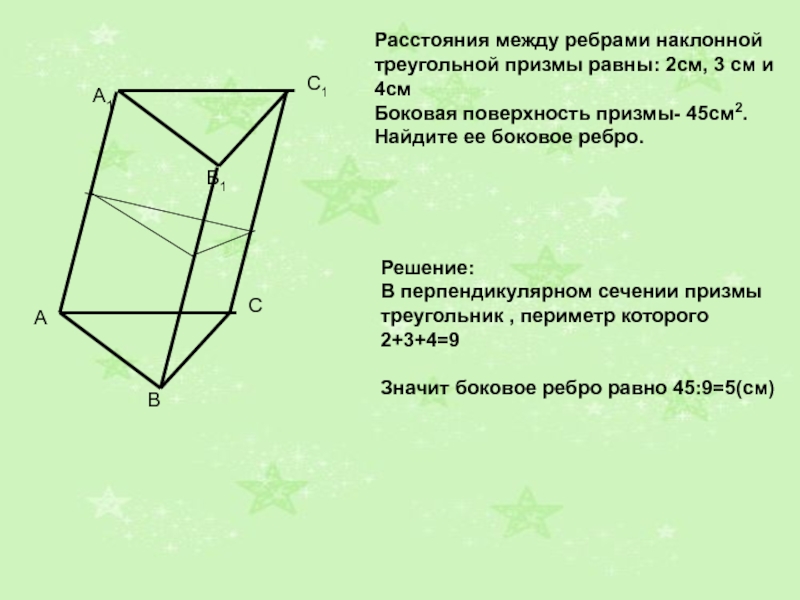
Расстояния между ребрами наклонной
треугольной призмы равны: 2см, 3 см и
4см
Боковая поверхность призмы- 45см2.Найдите ее боковое ребро.
Решение:
В перпендикулярном сечении призмы
треугольник , периметр которого 2+3+4=9Значит боковое ребро равно 45:9=5(см)