Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойство биссектрисы равнобедренного треугольника
Содержание
- 1. Свойство биссектрисы равнобедренного треугольника
- 2. Свойство биссектрисы равнобедренного треугольникаПовторение.Треугольник, у которого
- 3. Теорема: В равнобедренном треугольнике биссектриса, проведенная к
- 4. Свойство биссектрисы равнобедренного треугольникаAСDBБиссектрисаМедианаВысотаБиссектриса равнобедренного треугольника,
- 5. Свойство биссектрисы равнобедренного треугольникаЗадача. В
- 6. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Свойство биссектрисы равнобедренного
треугольника
Задачи для школьников:
Знать свойство
биссектрисы равнобедренного треугольника.
Слайд 2Свойство биссектрисы равнобедренного
треугольника
Повторение.
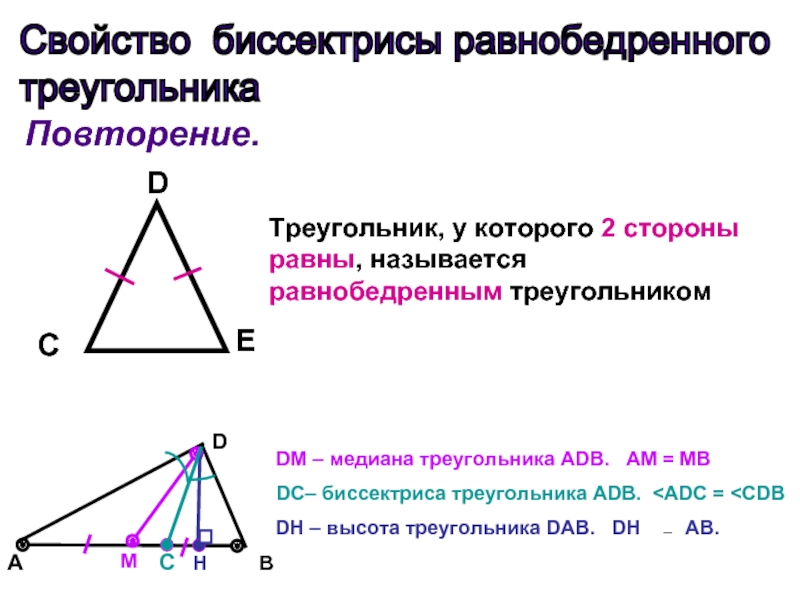
Треугольник, у которого 2 стороны равны, называется
равнобедренным треугольником
D
С
E
B
D
A
C
H
M
DM – медиана треугольника АDВ. AM = MB
DC– биссектриса треугольника АDВ. DH – высота треугольника DAB. DH AB.
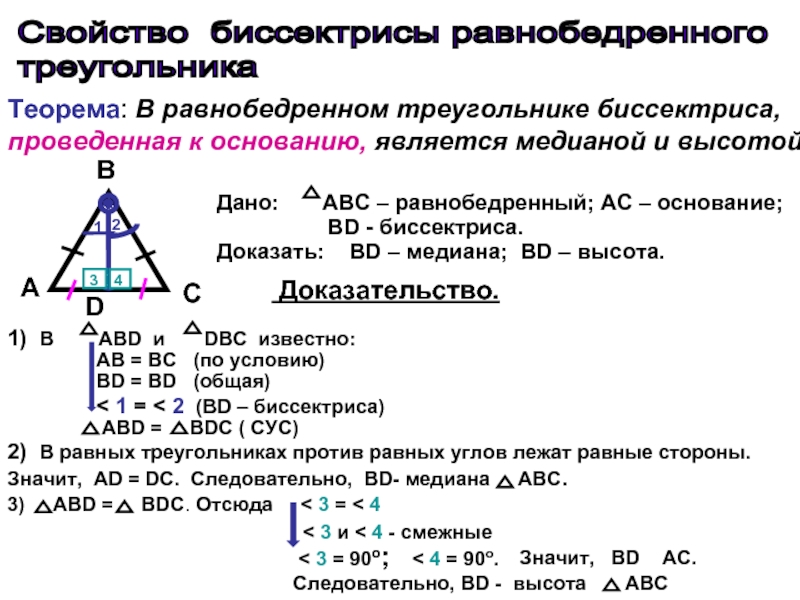
Слайд 3Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой
и высотой.
A
С
B
Дано: ABC – равнобедренный; АC –
основание;BD - биссектриса.
Доказать: BD – медиана; BD – высота.
Доказательство.
1
2
1) В ABD и DBC известно:
AB = BC (по условию)
BD = BD (общая)
< 1 = < 2 (BD – биссектриса)
ABD = ВDС ( СУС)
2) В равных треугольниках против равных углов лежат равные стороны. Значит, АD = DС. Следовательно, BD- медиана ABC.
D
Свойство биссектрисы равнобедренного
треугольника
3) ABD = ВDС. Отсюда < 3 = < 4
4
3
< 3 и < 4 - смежные
< 3 = 90о; < 4 = 90о.
Значит, BD AC.
Следовательно, BD - высота ABC
Слайд 4Свойство биссектрисы равнобедренного
треугольника
A
С
D
B
Биссектриса
Медиана
Высота
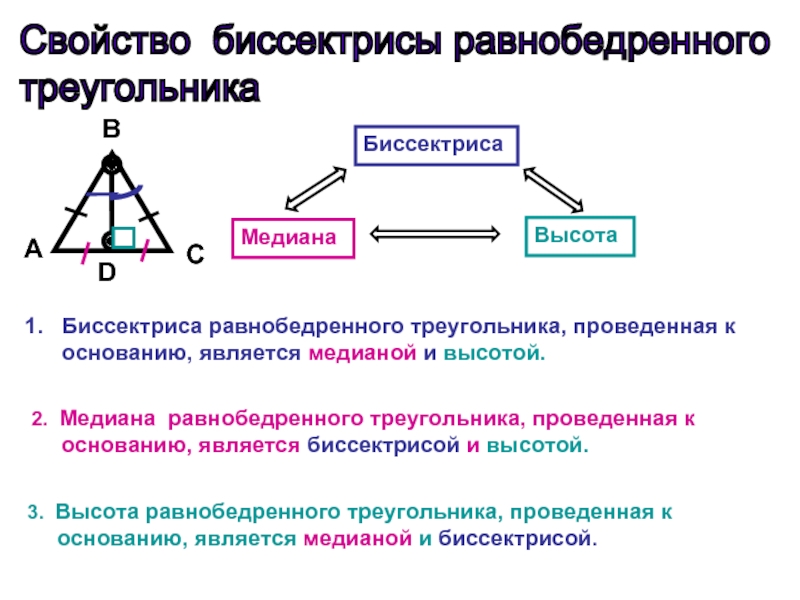
Биссектриса равнобедренного треугольника, проведенная к основанию, является
медианой и высотой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является
биссектрисой и высотой.3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Слайд 5Свойство биссектрисы равнобедренного
треугольника
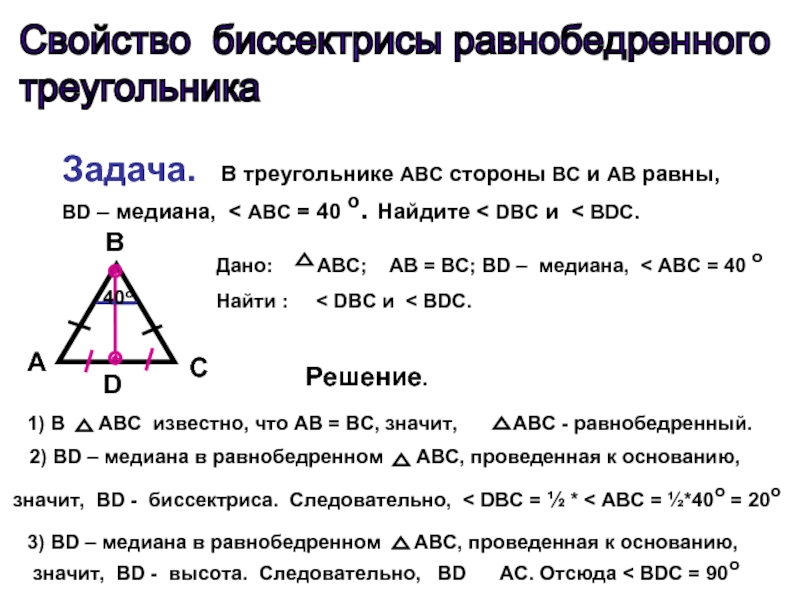
Задача. В треугольнике ABC стороны ВС
и АВ равны, BD – медиана, < АВС = 40
о. Найдите < DBC и < BDC.A
С
B
D
Дано: ABC; AB = BC; BD – медиана, < АВС = 40 о
Найти : < DBC и < BDC.
Решение.
1) В АВС известно, что АВ = ВС, значит, АВС - равнобедренный.
2) BD – медиана в равнобедренном АВС, проведенная к основанию,
значит, ВD - биссектриса. Следовательно, < DBC = ½ * < ABC = ½*40o = 20o
3) BD – медиана в равнобедренном АВС, проведенная к основанию,
значит, ВD - высота. Следовательно, BD AC. Отсюда < BDC = 90o
40о