Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак перпендикулярности прямой и плоскости 10 класс (по учебнику Атанасяна)
Содержание
- 1. Признак перпендикулярности прямой и плоскости 10 класс (по учебнику Атанасяна)
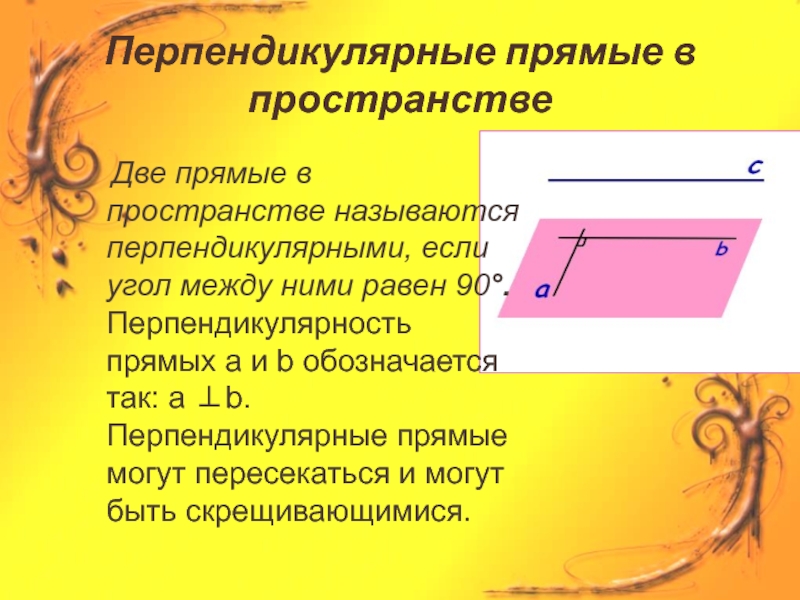
- 2. Перпендикулярные прямые в пространстве Две
- 3. Прямая называется перпендикулярной к плоскости, если
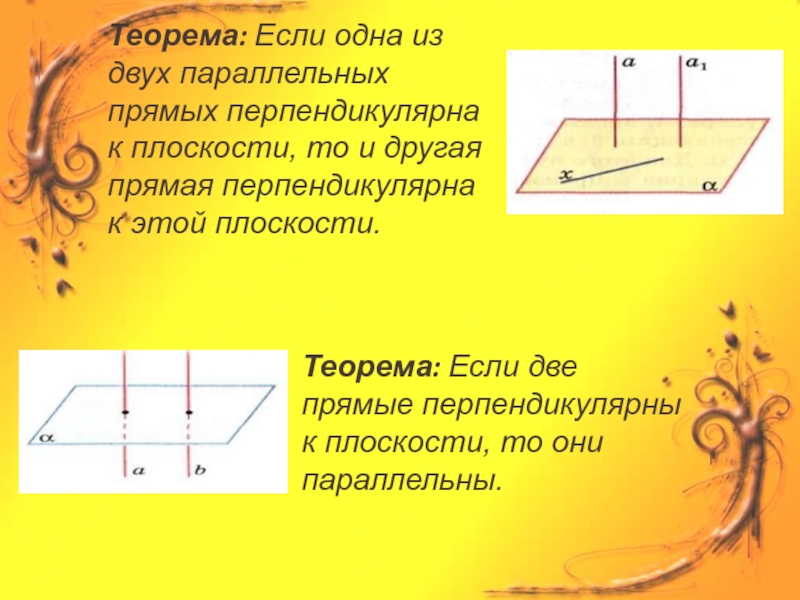
- 4. Теорема: Если две прямые перпендикулярны к плоскости,
- 5. Если прямая перпендикулярна к двум пересекающимся прямым,
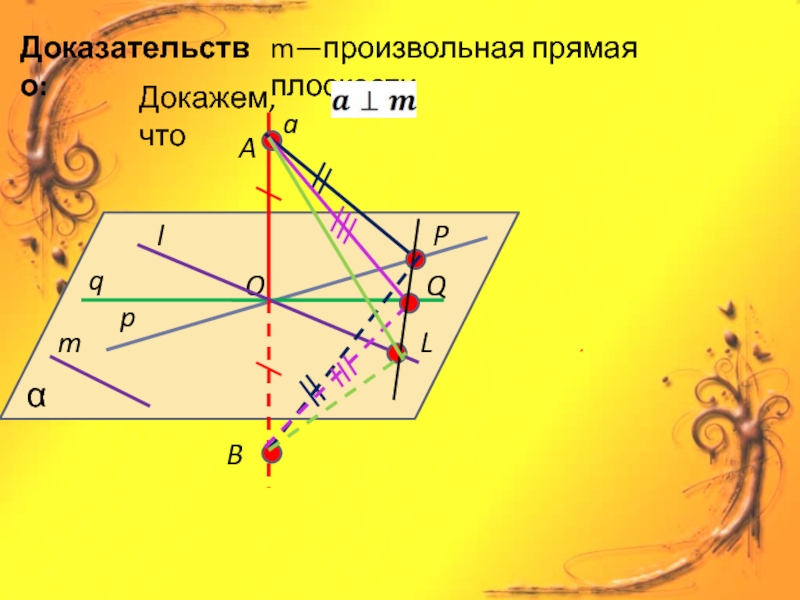
- 6. Доказательство:Om—произвольная прямая плоскости Докажем, что ABPQL
- 7. Скачать презентанцию
Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: а ⊥b. Перпендикулярные прямые могут пересекаться
Слайды и текст этой презентации
Слайд 3 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к
любой прямой, лежащей в этой плоскости.
Лемма
Если одна из двух параллельных
прямых перпендикулярна к этой прямой, то и другая прямая перпендикулярна к этой прямой
Слайд 4Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
Теорема:
Если одна из двух параллельных прямых перпендикулярна к плоскости, то
и другая прямая перпендикулярна к этой плоскости.
Слайд 5Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна к этой плоскости.
Дано:
Доказать:
Признак перпендикулярности
прямой и плоскости
