Решение прямоугольного треугольника

= cosB
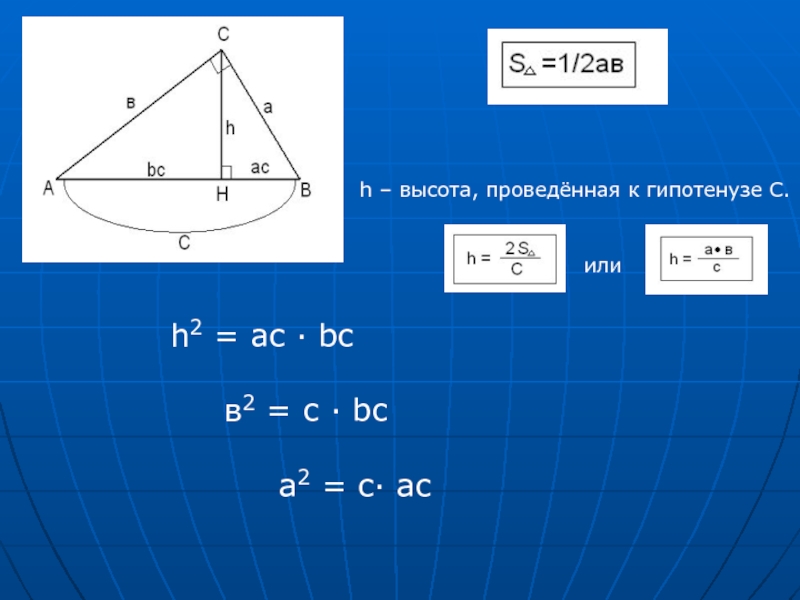
2)с2 = а2 + в2
3)а =

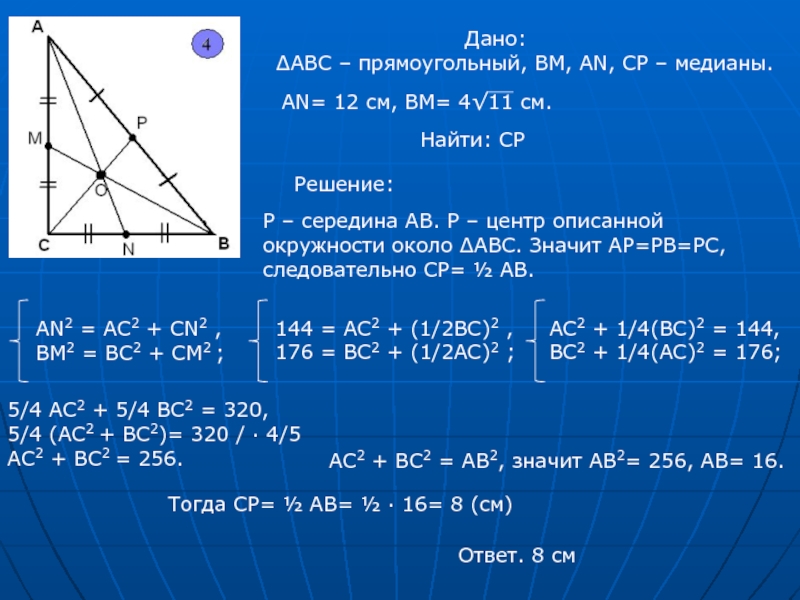
О – середина АВ ( О – центр описанной окружности)

R- радиус описанной окружности,
АВ- диаметр описанной окружности.

r- радиус вписанной окружности

∙ bc

в2 = c ∙ bc

∟HCC1
Биссектриса прямого угла делит угол между высотой и медианой пополам,

),
CH – высота

АС = 10, АH =

Найти: S∆АВС

Решение:

1) ∆АCH: AH= 8; AC= 10; CH= √AC2 – AH2 = √102 – 82 = √36 = 6

2) CH2 = AH ∙ HB, HB= CH2/AH = 62/8 = 9/2 = 4.5

3) AB = AH + HB = 8 + 4.5 = 12.5

4) S∆= 1/2АB ∙ CH= 1/2 ∙ 6 ∙ 12.5= 37.5

Ответ. 37.5

расстояние от точки пересечения медиан прямоугольного треугольника до его гипотенузы.
АВ=

Решение:

Проведём CH – высоту, тогда ОТ

OH, как перпендикуляры, проведённые к АВ.

Значит ∆ОТМ ∞ ∆ОHМ, следовательно

СМ – медиана, значит

ОМ / CM= 1/3

Тогда ОТ / CH= 1/3, т.к. CH- высота, проведённая из вершины прямого угла, то
CH= AC∙ BC / AB

AC = √AB2 – BC2 = √ 252- 202 = √225 = 15 (см)

CH= 15 ∙ 20 /25= 12 (см)

OT= CH / 3= 12/3= 4 (см)

Ответ. 4 см

6см. Найти диаметр описанной окружности.
Дано:
∆АВС – прямоугольный ( ∟С

P= 72см, r = 6см.

Найти: АВ

Решение:

АВ- диаметр описанной окружности. О - центр вписанной окружности ( точка пересечения биссектрис углов).

r = 6, (а + в – с)/ 2 = 6

P= а + в + с, а + в = P – c = 72 – c , тогда

(72 –с –с)/ 2= 6,
72 -2c = 12,
2c= 60,
C=30, AB= 30.

Ответ. 30 см

Дано:
∆АВС – прямоугольный, ВМ, АN,

АN= 12 см, ВМ= 4√11 см.

Найти: СР

Решение:

Р – середина АВ. Р – центр описанной окружности около ∆АВС. Значит АР=РВ=РС, следовательно СР= ½ AB.

AN2 = AC2 + CN2 ,
BM2 = BC2 + CM2 ;

144 = AC2 + (1/2BC)2 ,
176 = BC2 + (1/2AC)2 ;

AC2 + 1/4(BC)2 = 144,
BC2 + 1/4(AC)2 = 176;

5/4 AC2 + 5/4 BC2 = 320,
5/4 (AC2 + BC2)= 320 / ∙ 4/5
AC2 + BC2 = 256.

AC2 + BC2 = AB2, значит AB2= 256, АВ= 16.

Тогда СР= ½ AB= ½ ∙ 16= 8 (см)

Ответ. 8 см

Дано:
∆АВС – прямоугольный ( ∟С

Найти: S∆АВС

Решение:

S∆АВС = ½ AC ∙ BC

S∆СBM = ½ MC ∙ BC , ½ MC ∙ BC = 8, MC ∙ BC = 16. (1)

sinA= 0.8, значит cosB= 0.8

tgв/2= √1- cosB / √1+ cosB= √1- 0.8 / √1+ 0.8= √0.2/1.8= √1/9= 1/3

tgв/2= MC/BC, MC/BC= 1/3, MC= 1/3 BC. (2)

Подставим в (1) равенство, получим: BC ∙ 1/3BC= 16, 1/3 BC2= 16

Значит BС2= 48, ВС= 4√3 (см)

∆АВС: BC= 4√3, sinA= 0.8

: 0.8 / √1-(0.8)2=
= 4√3 ∙ 0.6/0.8= 3√3 (см).
S∆АВС= ½

Ответ. 18 (см)2

прямого угла, равна 3, АС= 5. Найти SABC

2) В прямоугольном треугольнике АВС(∟С= 900), проведена биссектриса ВК. Найти 9√5S, где S- площадь ∆СВК. S∆ABC= 3√5, а sinA= 2/7.
Ответ. 63.

3) В прямоугольном треугольнике АВС(∟С= 900). Через центр О – вписанной в треугольник окружности проведён луч ВО, пересекающий катет АС в точке М. Известно, что АМ= 8√3, ∟А= ∟МВС. Найти гипотенузу.
Ответ. 24.

второго катета на гипотенузу равна 16см. Найти диаметр окружности, описанной

5) Гипотенуза АВ прямоугольного треугольника АВС равна 2√22, а катет ВС равен 6.
Найти длину медианы ВК.
Ответ. 7.