Решение задач на применение признаков равенства треугольников

треугольника:
а)медиана б)биссектриса

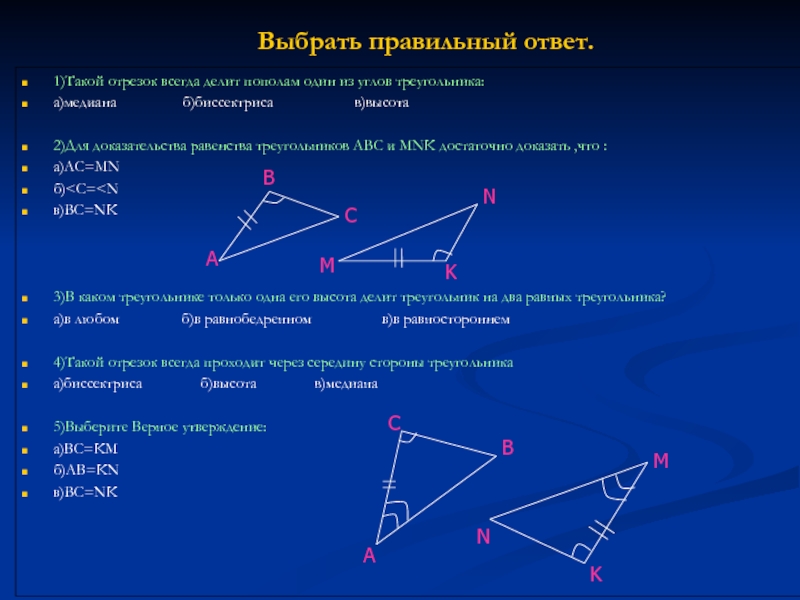
в)высота

2)Для доказательства равенства треугольников АВС и MNK достаточно доказать ,что :
а)AC=MN
б)в)BC=NK



3)В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а)в любом б)в равнобедренном в)в равностороннем

4)Такой отрезок всегда проходит через середину стороны треугольника
а)биссектриса б)высота в)медиана

5)Выберите Верное утверждение:
а)BC=KM
б)AB=KN
в)BC=NK

AO=4 см
BC=5

см
CD=4,5 см

Найти : P ABO

№ 1

Евклид, и оно несколько отлично от равенства в арифметике или

алгебре. Определение «равенства» фигур содержится в первой книге «Начал»: «совмещающиеся друг с другом равны между собой». Итак, под равенством фигур Евклид, а вслед за ним другие геометры понимали возможность совмещения фигур наложением.

Признаки равенства треугольников имели издавна важнейшее значение в геометрии. Так как доказательство многочисленных теорем сводится к доказательству равенству тех или иных треугольников.

Милетским (ок. 625 – ок. 547 гг. до н.э.). Известно,

что в молодости Фалес совершил поездку в Египет, и обучался там, в школах Мемфиса и Фив. Вернувшись в Милет он создает свою ионийскую школу. Считается что именно Фалес Милетский научил греков геометрии. Именно ему приписывается первое применение циркуля и угломера – большого транспортира, позволявшего измерять углы между двумя направлениями. Так же поразил египетских жрецов своим определением высоты пирамиды Хеопса. Он дождался момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды. Фалес первый вписал прямоугольный треугольник в круг. Помимо математики Фалес был хорошим астрономом, географом и т.д. До нашего времени не дошли сочинения Фалеса. Однако ему приписываются следующие теоремы:

круг делится диаметром пополам;
углы при основании равнобедренного треугольника равны;
противоположные углы между двумя пересекающимися прямыми (т.е. вертикальные углы) равны; и другие теоремы.

по двум углам и прилежащей к ним стороне.
Эту теорему

Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно. Предполагают, что его способ состоял в следующем: пусть A – точка берега, B – корабль на море. Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC AB; в противоположном направлении восстанавливают CE AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB. Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).

сторонам и углу между ними) и третьего признака равенств треугольников

(по трем соответственно равным сторонам), практически ничего не известно. Предполагается, что этим занимались пифагорейцы, ученики пифагорейской школы, последователи Пифагора. Однако более точных имен и сведений о людях которые нашли и доказали эти две теоремы до наших дней не дошло.
Доподлинно известно, что Пифагору и его ученикам удалось сделать множество открытий и теорем. Из геометрических работ пифагорейцев на первом месте стоит знаменитая теорема Пифагора. Но ведь кроме математики они занимались философией, космологией и астрономией, так же сам Пифагор основал математическое учение о музыкальной гармонии.

№141; №142.
Дополнительная Задача:
Два равнобедренных треугольника ABC и ADC имеют общее

основание AC.
Вершины B и D расположены по разные стороны от AC.Точка E лежит на
отрезке BD, но не лежит на отрезке AC.
Докажите ,что