Симметрия

Математически строгое представление о симметрии сформировалось сравнительно недавно - в

19 веке. В наиболее простой трактовке современное определение симметрии выглядит примерно так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали (Г.Вейлю). 

Виды симметрии:
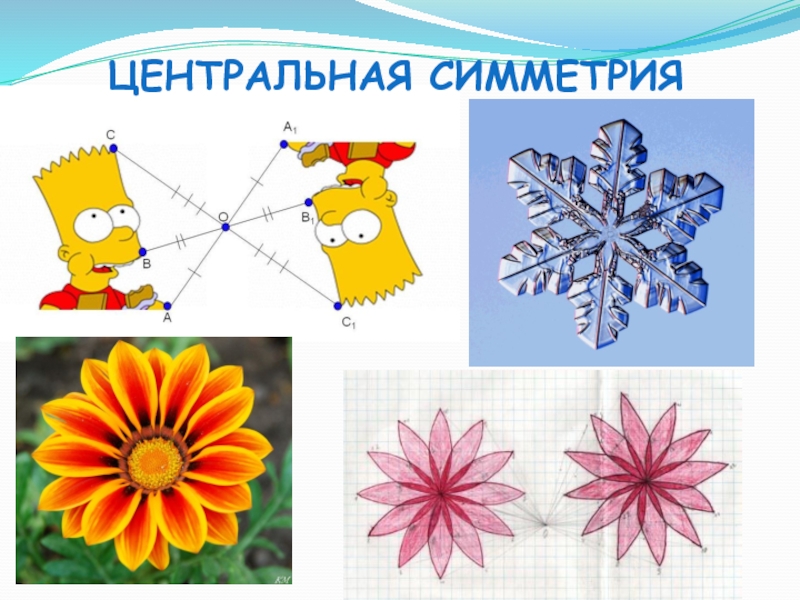
центральная симметрия (или симметрия относительно точки)
осевая симметрия (или симметрия относительно прямой)
зеркальная симметрия
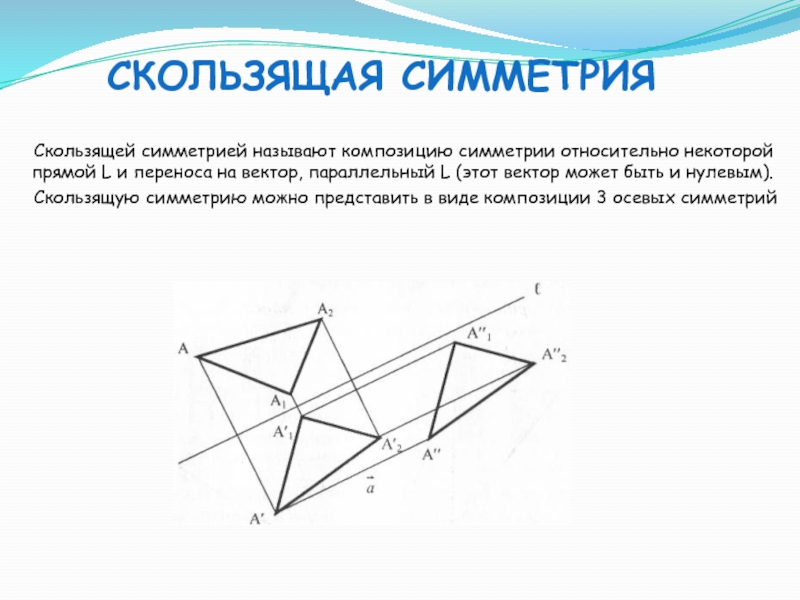
скользящая симметрия
винтовая симметрия

единственная точка (О – центр симметрии) остаётся на месте, остальные

же точки меняют своё положение: вместо точки А получаем точку А1 такую, что точка О середина отрезка АА1. Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно точки О, нужно через каждую точку фигуры Ф провести луч, проходящий через точку О (центр симметрии), и на этом луче отложить точку, симметричную выбранной относительно точки О. Множество построенных таким образом точек даст фигуру Ф1. 

Центральная симметрия

O

Q

Q1

точки прямой р остаются на месте (эта прямая является осью

симметрии), остальные же точки меняют своё положение: вместо точки В получаем такую точку В1, что прямая р является серединным перпендикуляром к отрезку ВВ1. Чтобы построить фигуру Ф1, симметричную фигуре Ф, относительно прямой р, нужно для каждой точки фигуры Ф построить точку, симметричную ей относительно прямой р. Множество всех этих построенных точек и дают искомую фигуру Ф1.

Осевая симметрия

точки одной плоскости сохраняют своё местоположение (α-плоскость симметрии), остальные точки

пространства меняют своё положение: вместо точки С получается такая точка С1, что плоскость α проходит через середину отрезка СС1, перпендикулярно к нему. 
Чтобы построить фигуру Ф1,симметричную фигуре Ф относительно плоскости α, нужно для каждой точки фигуры Ф выстроить симметричные относительно α точки, они в своём множестве и образуют фигуру Ф1.

Зеркальная симметрия

вектор может быть и нулевым).
Скользящую симметрию можно

представить в виде композиции 3 осевых симметрий

Скользящая симметрия

вдоль этой оси.
Винтовая симметрия

В Е З К С Э Ю - горизонтальная ось

Палиндромы:
Доход, казак,

мадам, комок, радар, шалаш, потоп и др.
А роза упала на лапу Азора.
Хил, худ, а дух лих.
Леша на полке клопа нашел.
Нажал кабан на баклажан.
У дуба буду.
Он в аду давно.

Симметрия в русском языке и литературе