Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства параллелограмма
Содержание
- 1. Свойства параллелограмма
- 2. Свойство 1. В параллелограмме противоположные
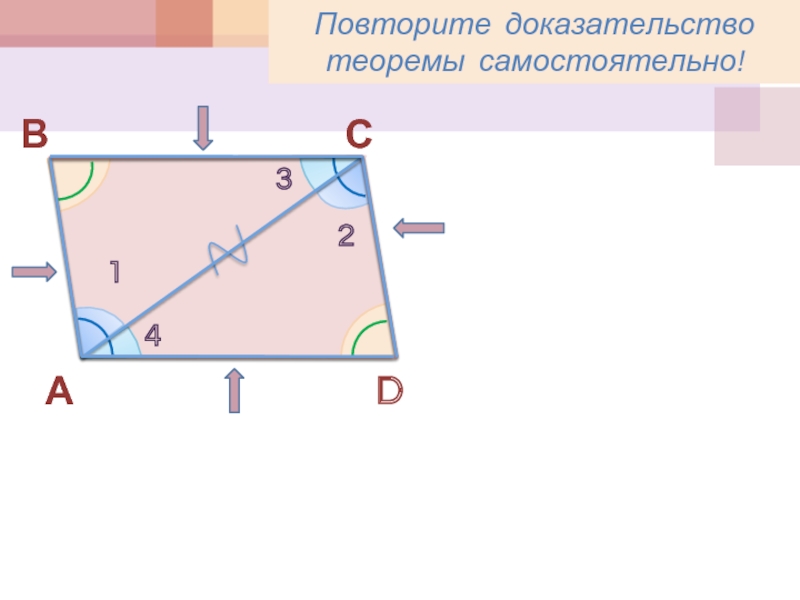
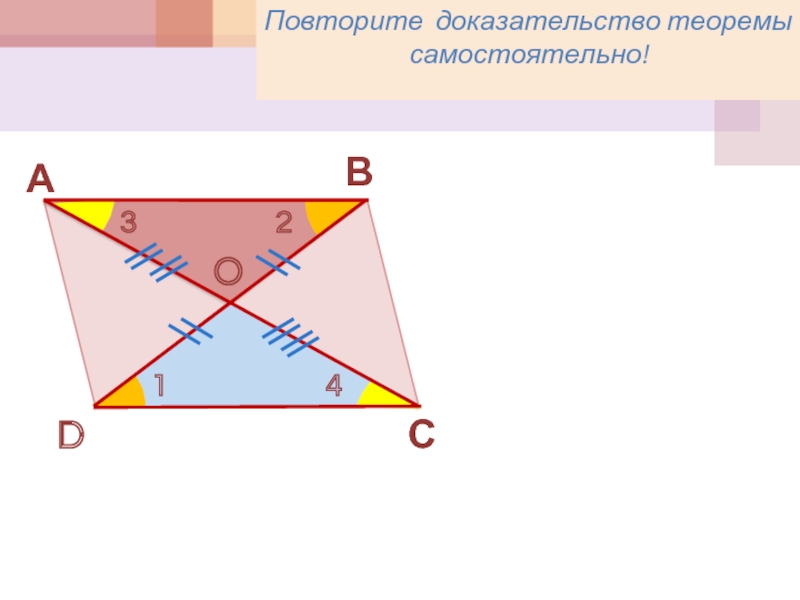
- 3. АСВD1234Повторите доказательство теоремы самостоятельно!
- 4. Решите задачи1MNPK7 см 4 см Найдите периметр параллелограмма MNPK270Найдите все углы параллелограмма MNPK
- 5. АВ СD, ВD, AC – секущие
- 6. ВАСD1234OПовторите доказательство теоремы самостоятельно!
- 7. Решите задачу. В параллелограмме ABCD:
- 8. Литература Л. С. Атанасян, В. Ф. Бутузов
- 9. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Геометрия 8 класс
Свойства параллелограмма
(приложения к уроку)
Сокирко Светлана Петровна
учитель математики
и физики
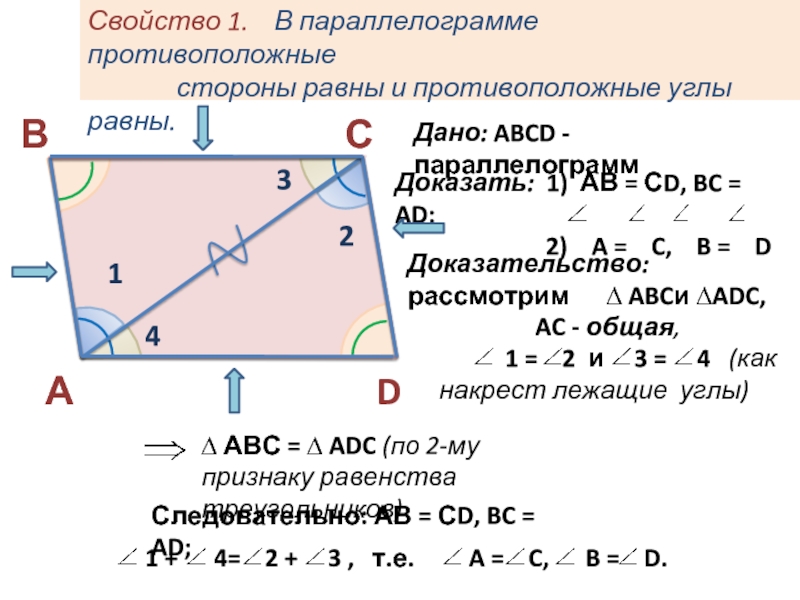
Слайд 2Свойство 1. В параллелограмме противоположные
стороны равны и противоположные углы равны.
А
С
В
D
1
2
3
4
Дано: ABCD
- параллелограммДоказать: 1) АВ = СD, BC = AD;
2) A = C, B = D
Доказательство: рассмотрим ∆ ABCи ∆ADC,
AC - общая,
1 = 2 и 3 = 4 (как накрест лежащие углы)
∆ АВС = ∆ ADC (по 2-му признаку равенства треугольников)
Следовательно: АВ = СD, BC = AD;
1 + 4= 2 + 3 , т.е. A = C, B = D.
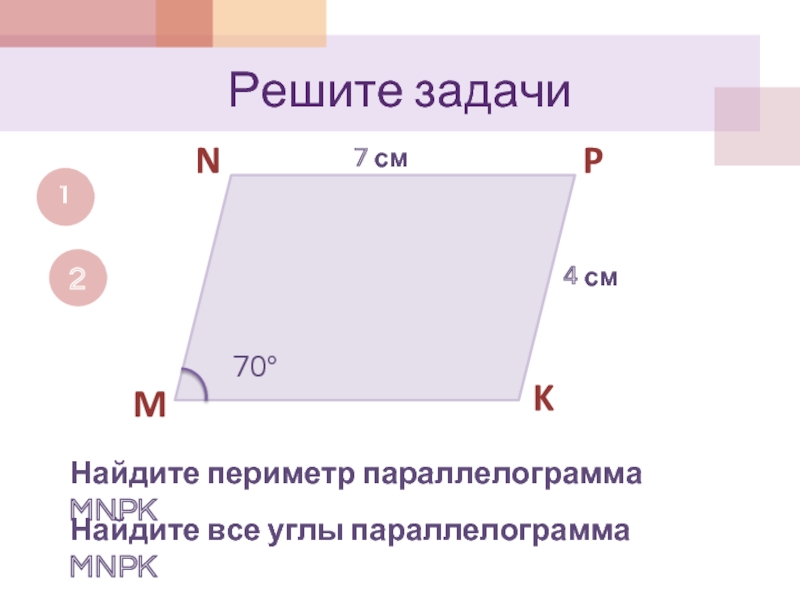
Слайд 4Решите задачи
1
M
N
P
K
7 см
4 см
Найдите периметр параллелограмма MNPK
2
70
Найдите все
углы параллелограмма MNPK
Слайд 5АВ СD, ВD, AC – секущие
1= 2 и 3=
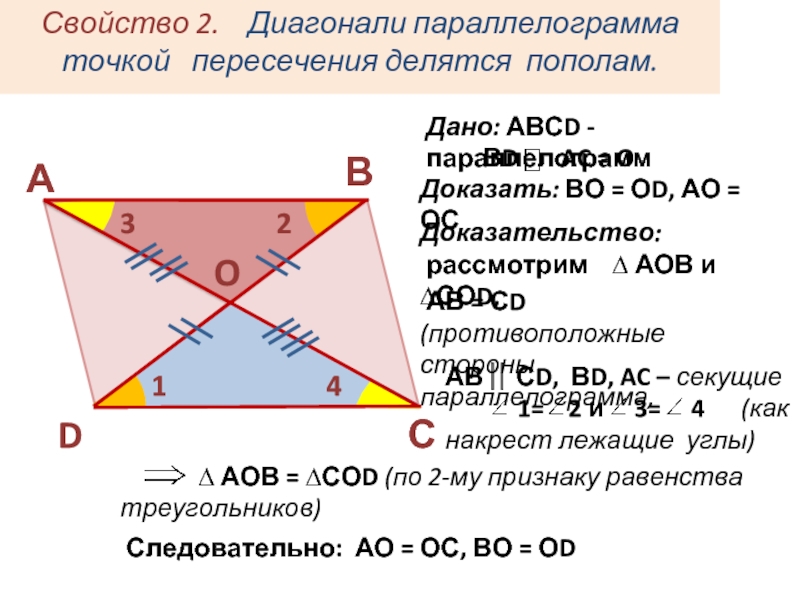
4 (как накрест лежащие углы)Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
В
А
С
D
1
2
3
4
Дано: АВСD - параллелограмм
ВD AC = O
Доказать: ВО = ОD, АО = ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
∆ АОВ = ∆СОD (по 2-му признаку равенства треугольников)
O
АВ = СD (противоположные стороны параллелограмма,
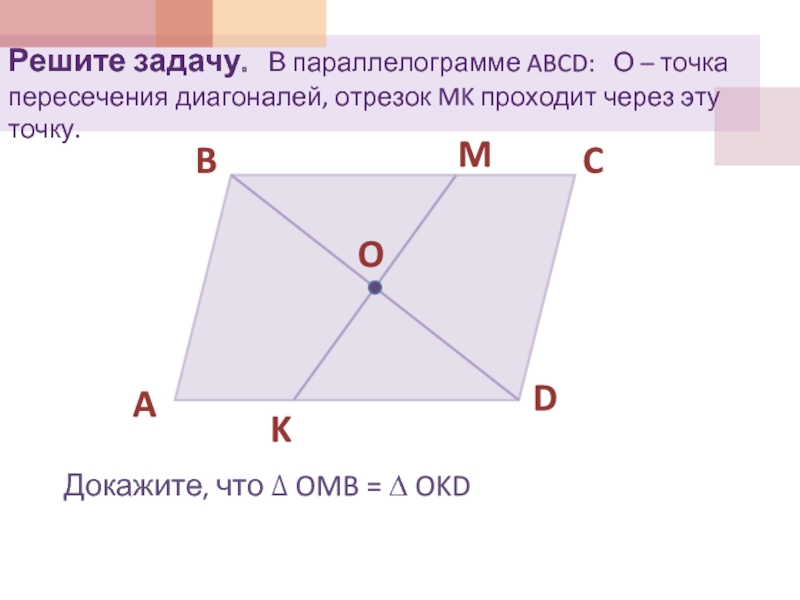
Слайд 7Решите задачу. В параллелограмме ABCD: О – точка
пересечения диагоналей, отрезок MK проходит через эту точку.
1
A
B
C
D
2
Докажите, что ∆
OMB = ∆ OKD O
K
M
Слайд 8Литература
Л. С. Атанасян, В. Ф. Бутузов и др.
Геометрия 7-9
Н. Ф. Гаврилова. Поурочные разработки по геометрии: 8
класс. M.: ВАКО, 2004. – 288с. – (В помощь школьному учителю)Мельникова Н. Б., Лепихова М. Тематический контроль по геометрии. 8 кл. - М.: Интеллект-Центр. 2007.