Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что изучает геометрия 7 класс
Содержание
- 1. Что изучает геометрия 7 класс
- 2. Мы узнаем откуда пришла, и какой раньше была геометрия.
- 3. Прежде, чем идти на урок. Давайте узнаем историю геометрии и области ее применения.
- 4. Геоме́трия (от греч. γη — Земля и
- 5. Муза геометрии, Лувр
- 6. История геометрии.Традиционно считается, что родоначальниками геометрии являются
- 7. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века.
- 8. Геометрия в Древнем Египте.
- 9. Vпрям. параллелепипеда
- 10. V = 1/6aS S - площадь
- 11. «…теоретическое естествознание, если оно хочет проследить историю
- 12. Геометрия в Древней Греции.
- 13. Фалес Милетский (ок.625 – 547 до н. э.) первый греческий геометр
- 14. По–гречески скалку называли «каландер», поэтому все тела
- 15. Слово «параллельный» происходит от греческого «параллелос» -
- 16. Геометрия в Древнем Вавилоне.
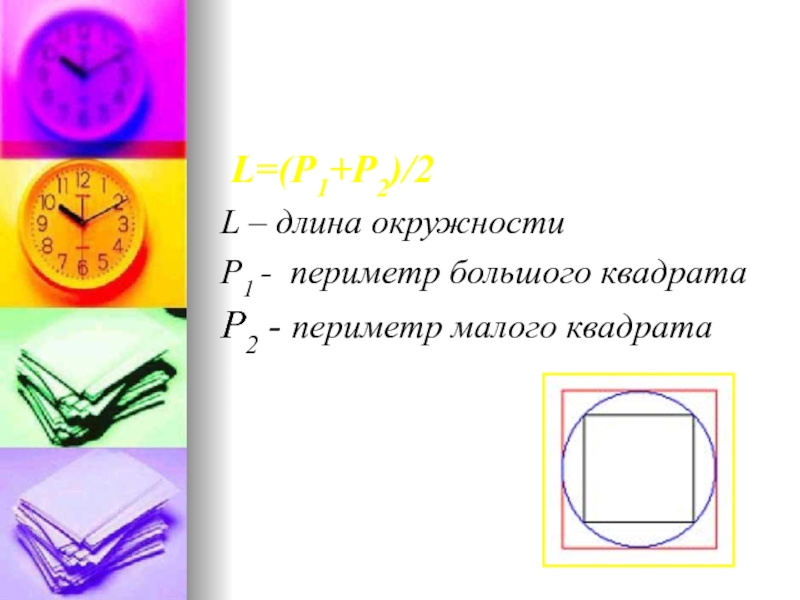
- 17. L=(Р1+Р2)/2L – длина окружностиР1 - периметр большого квадратаР2 - периметр малого квадрата
- 18. И в заключении. Самое древнее сочинение,
- 19. Скачать презентанцию
Мы узнаем откуда пришла, и какой раньше была геометрия.
Слайды и текст этой презентации
Слайд 4Геоме́трия (от греч. γη — Земля и μετρεω — мера,
измерение) — раздел математики, изучающий пространственные отношения и их обобщения. В
геометрии можно условно выделить следующие разделы: Классическая геометрия — геометрия точек, прямых и плоскостей, а также фигур на плоскости и тел в пространстве. Включает в себя планиметрию, стереометрию.и.т.д.. Аналитическая геометрия — геометрия координатного метода. Изучает линии, векторы, фигуры и преобразования, которые задаются алгебраическими уравнениями в аффинных или декартовых координатах, методами алгебры. Дифференциальная геометрия изучает линии и поверхности, задающиеся дифференцируемыми функциями, а также их отображения. Топология — наука о понятии непрерывности в самом общем виде.Слайд 6История геометрии.
Традиционно считается, что родоначальниками геометрии являются древние греки, перенявшие
у египтян ремесло землемерия и измерения объёмов тел и превратившие
его в науку. Превращение это произошло путём абстрагирования от всяких свойств тел, кроме взаимного положения и величины. Наукой геометрия стала, когда от набора рецептов перешли к установлению общих закономерностей. Греки составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд и поныне остаётся образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом. Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием.Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Ф. Клейн связал все виды геометрий, согласно ему геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.
Слайд 7Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал»,
начало XIV века.
Слайд 9
Vпрям. параллелепипеда = S *
h
V – объём
S – площадь основания
h – высота
Sкруга = (8/9
d)2 = 64/81d2d – поперечник круга (диаметр)
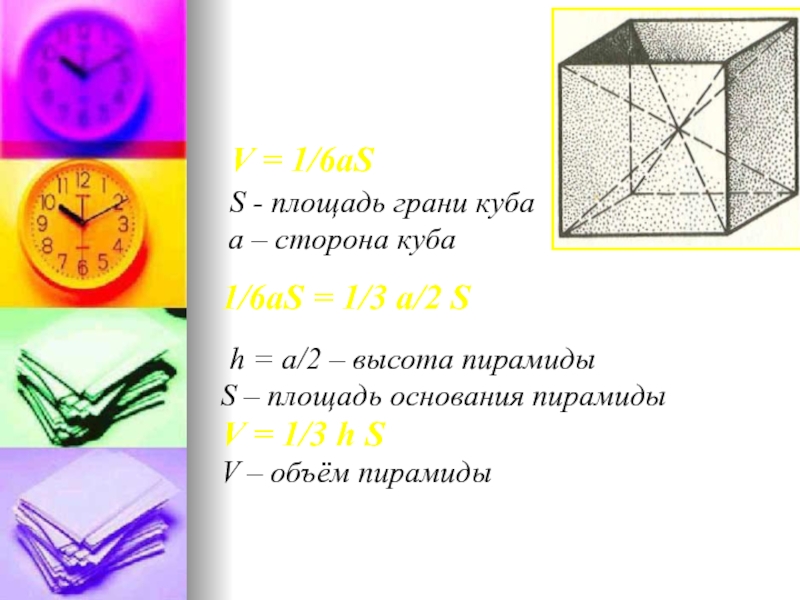
Слайд 10 V = 1/6aS
S - площадь грани куба
а
– сторона куба
1/6aS = 1/3 а/2 S
h =
а/2 – высота пирамидыS – площадь основания пирамиды
V = 1/3 h S
V – объём пирамиды