Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Средняя линия треугольника
Содержание
- 1. Средняя линия треугольника
- 2. Каким образом эти треугольники поделили на две группы?
- 3. АBCОтрезок, соединяющий середины двух сторон,называют СРЕДНЕЙ ЛИНИЕЙ
- 4. Теорема. Средняя линия треугольника параллельна одной из
- 5. Найдите периметр треугольника АВС.АСВ7 смFNO148 см5,5см1611Запомни!
- 6. АВСDОКПроверка:АО = ОСВК = КСКО - средняя
- 7. BАDОпределите вид четырехугольника, который получится от последовательного
- 8. Слайд 8
- 9. Какие новые знания получены на уроке?Что называют
- 10. Домашнее задание: Задачи № 566, 568 (а)
- 11. Скачать презентанцию
Каким образом эти треугольники поделили на две группы?
Слайды и текст этой презентации
Слайд 3
А
B
C
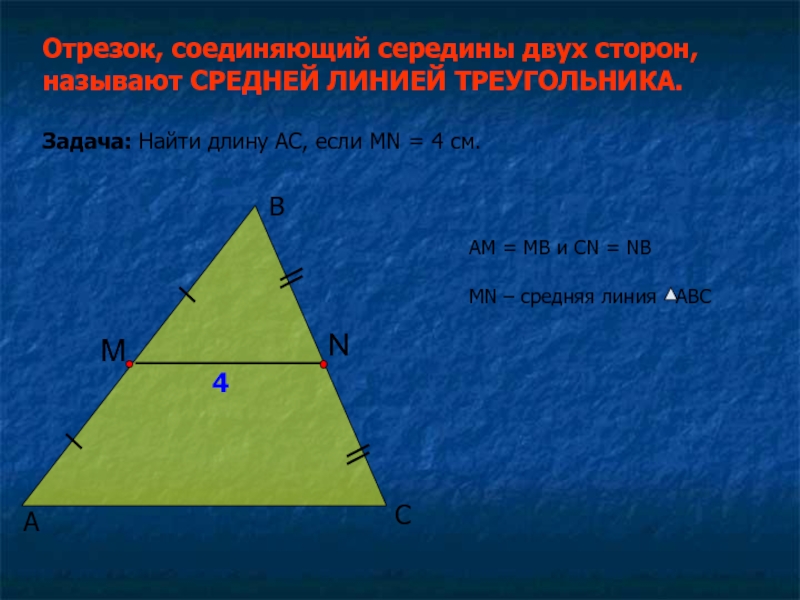
Отрезок, соединяющий середины двух сторон,
называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Задача: Найти длину
АС, если MN = 4 см.
4
AM = MB и CN
= NBMN – средняя линия ABC
Слайд 4
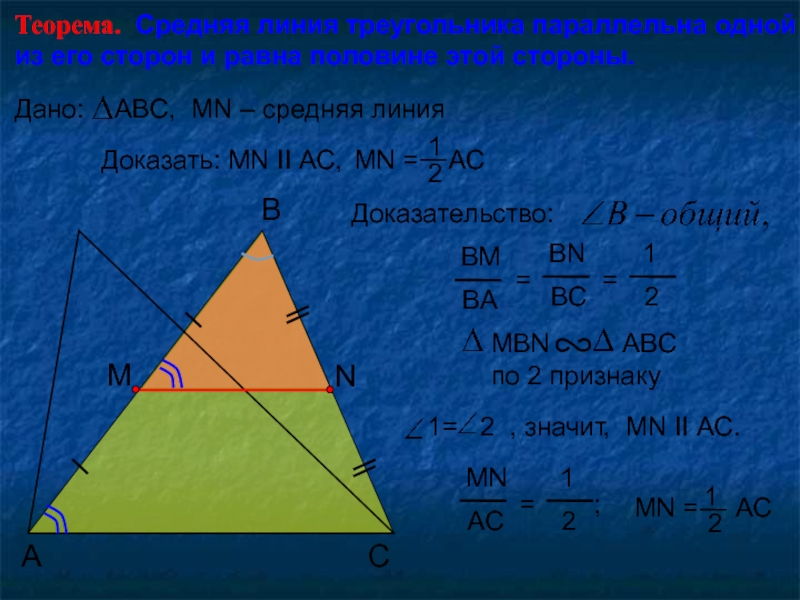
Теорема. Средняя линия треугольника параллельна одной из его сторон и
равна половине этой стороны.
Доказательство:
А
B
C
MN = АС
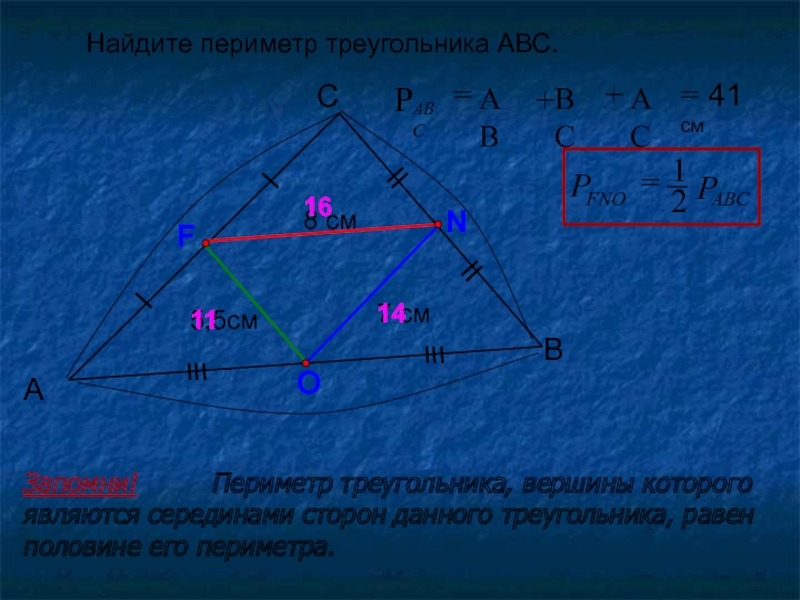
Слайд 5Найдите периметр треугольника АВС.
А
С
В
7 см
F
N
O
14
8 см
5,5см
16
11
Запомни!
Периметр треугольника, вершины которого являются серединами сторон данного треугольника, равен
половине его периметра.
Слайд 6
А
В
С
D
О
К
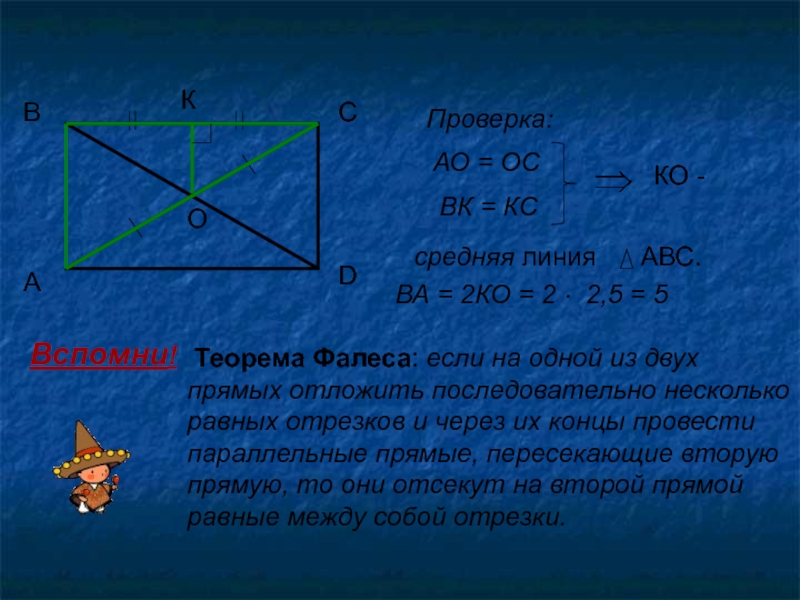
Проверка:
АО = ОС
ВК = КС
КО -
средняя линия
АВС.
ВА = 2КО
= 2 2,5 = 5
.
Вспомни!
Теорема Фалеса: если на
одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.2,5
?
Слайд 7
B
А
D
Определите вид четырехугольника, который получится от последовательного соединения середин сторон
любого выпуклого четырехугольника.
С
PQ – средняя линия ABD
EF –
средняя линия BDCPQ II BD
EF II BD
PQ II EF
PQ = BD
EF = BD
PQ = EF
PQFE – параллелограмм ( по I признаку )
7
Слайд 9Какие новые знания получены на уроке?
Что называют средней линией треугольника?
Сформулируйте
теорему о средней линии треугольника.
Итог урока
Слайд 10Домашнее задание:
Задачи № 566, 568 (а)
П. 62, вопрос
8
Дополнительная задача:
В прямоугольном треугольнике АВС < C =
900, < A = 300,СВ = 6 см. Найти периметр треугольника, вершины которого являются серединами сторон данного треугольника.