Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства параллелепипеда
Содержание
- 1. Свойства параллелепипеда
- 2. Планиметрия
- 3. Противоположные грани параллелепипедапараллельны и равныABCDA1B1C1Дано: ABCDA1B1C1D1
- 4. Теорема: Противоположные грани параллелепипеда параллельны и
- 5. Теорема: Противоположные грани параллелепипеда параллельны и
- 6. Изучите доказательство, представленное в учебнике.
- 7. Оформите доказательство теоремы для граней AA1D1D и
- 8. Применение изученной теоремы при решении задачТеорема:
- 9. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Свойства параллелепипеда
Подготовила: Преподаватель математики ГБОУ СПО БППК
Плющева А.В.
2013г.
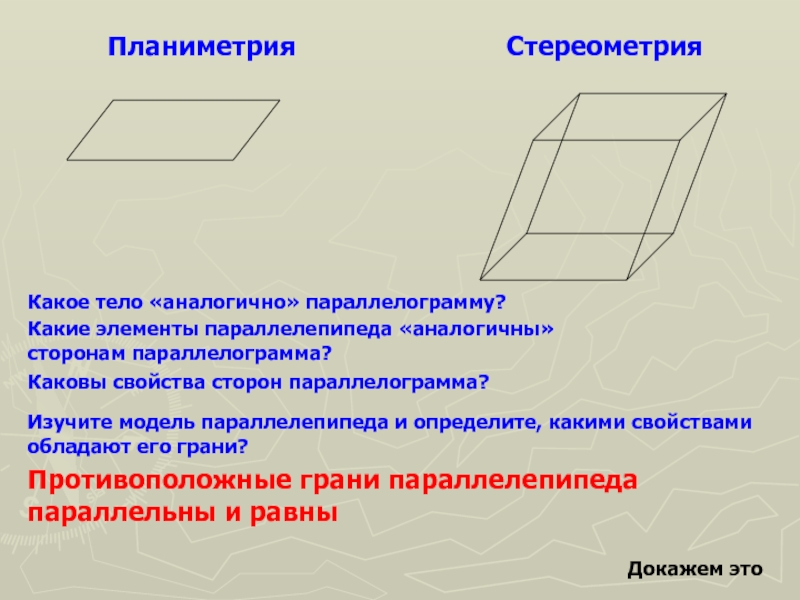
Слайд 2Планиметрия
Стереометрия
Какое тело «аналогично» параллелограмму?
Какие элементы параллелепипеда
«аналогичны»сторонам параллелограмма?
Каковы свойства сторон параллелограмма?
Изучите модель параллелепипеда и определите, какими свойствами обладают его грани?
Противоположные грани параллелепипеда параллельны и равны
Докажем это
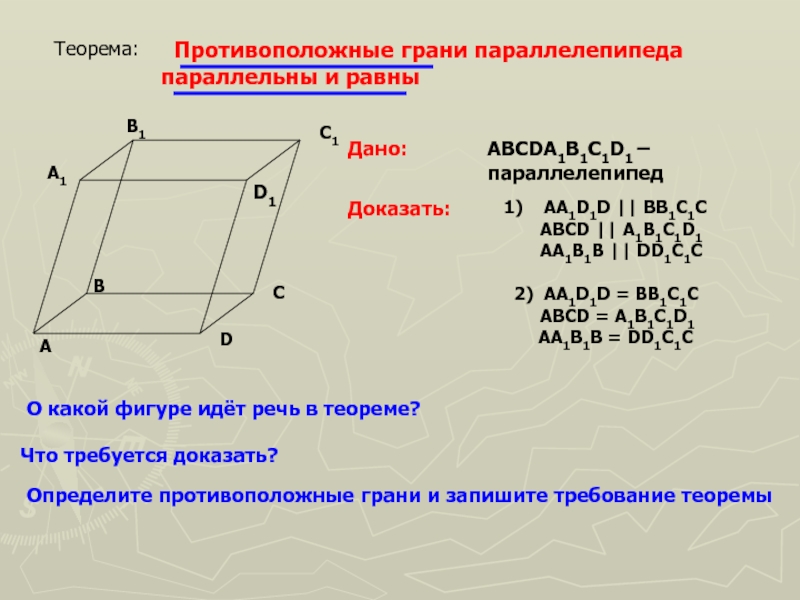
Слайд 3 Противоположные грани параллелепипеда
параллельны и равны
A
B
C
D
A1
B1
C1
Дано:
ABCDA1B1C1D1 – параллелепипед
Доказать:
AA1D1D ||
BB1C1C
ABCD || A1B1C1D1
AA1B1B ||
DD1C1C2) AA1D1D = BB1C1C
ABCD = A1B1C1D1
AA1B1B = DD1C1C
О какой фигуре идёт речь в теореме?
Что требуется доказать?
Определите противоположные грани и запишите требование теоремы
Теорема:
D1
Слайд 4
Теорема: Противоположные грани параллелепипеда параллельны и равны
A
D
C
B
A1
B1
C1
D1
Докажем параллельность граней
О
каких гранях идёт речь?
Сколько пар граней достаточно рассмотреть для
доказательства их
параллельности?Если взять грань AA1D1D, тогда какая будет ей противоположной?
BB1C1C
Что значит, что грани параллельны?
Лежат в параллельных плоскостях
Что используют для док-ва параллельности плоскостей?
Признак: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
Можно ли выделить такие пары прямых?
AA1 и BB1 , AD и BC
Из какой фигуры можно сделать вывод, что АА1|| BB1?
Почему AD||BC?
Что ещё нужно знать об выбранных прямых одной плоскости?
Они должны пересекаться
Какой вывод сделаем?
AA1D1D || BB1C1C
Одну
Выполняется это условие?
Слайд 5Теорема: Противоположные грани параллелепипеда параллельны и равны
Докажем равенство граней
О
каких гранях идёт речь?
А
В
С
D
A1
B1
C1
D1
Докажем для граней АА1D1D и ВВ1С1С.
В
каком случае два параллелограмма равны?Параллелограммы
Когда соответствующие элементы одного параллелограмма равны соответствующим другого параллелограмма
Сколько пар равных элементов достаточно найти?
3 пары
Можно ли взять стороны AD и AA1 и ∠A1AD параллелограмма АА1 D1D? Почему?
Тогда назовите соответствующие элементы второго параллелограмма
Какой сделаем вывод?
AA1D1D = BB1C1C
Это 2 смежные стороны и угол между ними
Будет ли выполнятся равенство соответствующих элементов?
∠A1AD = ∠ B1ВC, как углы с сонаправленными сторонами
Что представляют собой грани параллелепипеда?
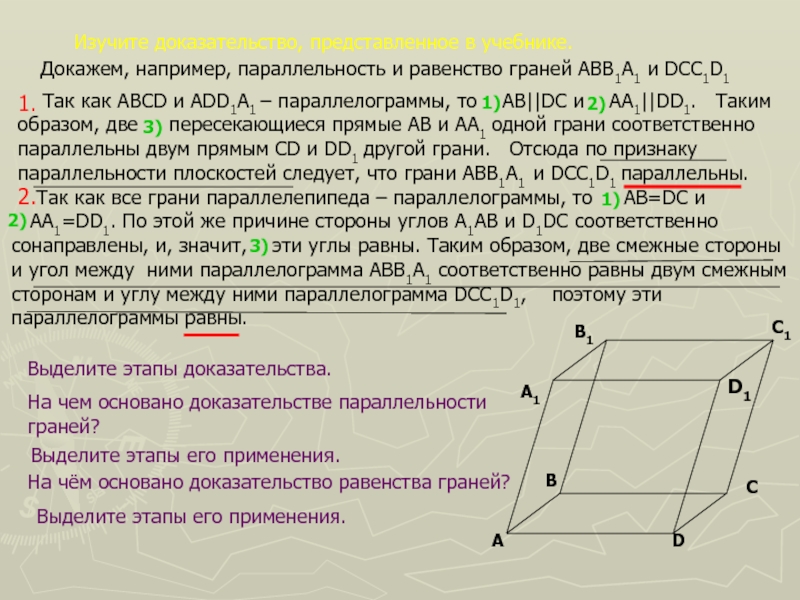
Слайд 6Изучите доказательство, представленное в учебнике.
Так как ABCD
и ADD1A1 – параллелограммы, то AB||DC и AA1||DD1.
Такимобразом, две пересекающиеся прямые AB и AA1 одной грани соответственно
параллельны двум прямым CD и DD1 другой грани. Отсюда по признаку
параллельности плоскостей следует, что грани ABB1A1 и DCC1D1 параллельны.
Так как все грани параллелепипеда – параллелограммы, то AB=DC и
AA1=DD1. По этой же причине стороны углов A1AB и D1DC соответственно сонаправлены, и, значит, эти углы равны. Таким образом, две смежные стороны и угол между ними параллелограмма ABB1A1 соответственно равны двум смежным сторонам и углу между ними параллелограмма DCC1D1, поэтому эти параллелограммы равны.
Выделите этапы доказательства.
1.
2.
1)
3)
1)
2)
3)
2)
На чем основано доказательстве параллельности граней?
На чём основано доказательство равенства граней?
A
B
C
D
A1
B1
C1
D1
Докажем, например, параллельность и равенство граней АВВ1А1 и DCC1D1
Выделите этапы его применения.
Выделите этапы его применения.
Слайд 7Оформите доказательство теоремы для граней AA1D1D и BB1C1C.
Теорема:
Противоположные грани параллелепипеда параллельны и равны
Дано: ABCDA1B1C1D1 - параллелограмм
Доказать:
1. ABCD || A1B1C1D1AA1B1B || DD1C1C
AA1D1D || BB1C1C
2. ABCD = A1B1C1D1
AA1B1B = DD1C1C
AA1D1D = BB1C1C
Сравните свое оформление с предложенным и сделайте выводы для себя
Слайд 8Применение изученной теоремы при решении задач
Теорема: Противоположные грани параллелепипеда
параллельны и равны
Дано: АВСDА1В1С1D1 - параллелепипед
АА1 = 6 см; AD
= 4 см∠A1AD = 60°
Найти: B1C
Дано: AD1 =8 см
A1D =6 см
AD1∩ A1D = O
∠AOD = 30°
Найти: CB
8
6
O
30
?
Решение:
A1D=√36+16-2*6*4*cos60°=√22
Т.к. A1D = B1C ,то B1C = √22
Решение:
AD=√16+9-2*3*4*cos30°=√25-12√3
Т.к. AD = BC, то BC =√25-12√3
Составьте задачу по чертежу
Решите задачу
Нанесите данные на чертеж
Решите задачу