Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства параллелограмма 8 класс
Содержание
- 1. Свойства параллелограмма 8 класс
- 2. Цель урока: организация деятельности обучающихся по формированию понятия «параллелограмм» и умению самостоятельно доказывать его свойства
- 3. Задачисоздать организационные и содержательные условия для усвоения
- 4. Результат обучения: воспроизведение своими словами определения параллелограмма,
- 5. Ход урокаОрганизационный момент (1-2 минуты)Актуализация знаний (5
- 6. Четырехугольники
- 7. Дано: параллелограмм АВСDДоказать: АD=СВ, DС=АВ, А=
- 8. ВыводВ параллелограмме противоположные стороны и углы равны.
- 9. Дано: параллелограмм АВСDДоказать: АО= СО, DО=ОВ.Доказательство: Рассмотрим
- 10. ВыводВ параллелограмме диагонали точкой пересечения делятся пополам
- 11. Дано: ABCD – параллелограмм Доказать: A
- 12. Дано:ABCD – параллелограмм
- 13. 3.Дано: ABCD – параллелограммБиссектриса D
- 14. Математический диктант Назвать фигуры, у которых
- 15. Математический диктант квадрат, прямоугольник квадрат, прямоугольник, ромб, параллелограмм квадрат, ромб квадрат, прямоугольник, ромб, параллелограмм квадрат, ромб
- 16. Критерии оценивания домашнего заданияОтметка «5» Если
- 17. Скачать презентанцию
Цель урока: организация деятельности обучающихся по формированию понятия «параллелограмм» и умению самостоятельно доказывать его свойства
Слайды и текст этой презентации
Слайд 1Конспект урока
«Свойства параллелограмма» (8 класс)
Автор: Банникова Татьяна Витальевна
Учитель
математики г. Екатеринбург
Слайд 2Цель урока:
организация деятельности обучающихся по формированию понятия «параллелограмм» и умению
самостоятельно доказывать его свойства
Слайд 3Задачи
создать организационные и содержательные условия для усвоения учащимися определения параллелограмм
способствовать
деятельности учащихся по самостоятельному доказательству свойств параллелограмма
создать условия по
развитию логического мышления, памяти, умения правильно обобщать данные и делать выводы, сравнивать и анализировать полученные выводысоздать условия для воспитания у обучающихся навыка работы в группах
воспитания чувства ответственности, самоконтроля
Слайд 4Результат обучения:
воспроизведение своими словами определения параллелограмма, развитие умения обобщать,
сравнивать, анализировать на примере доказательства свойств параллелограмма; развитие умения
решать задачи по теме «Параллелограмм», используя при решении доказательства свойств параллелограмма.Оборудование:
компьютер, мультимедийный проектор, презентация к уроку.
Слайд 5Ход урока
Организационный момент (1-2 минуты)
Актуализация знаний (5 минут)
Мотивация (3 минуты)
Изучение
нового материала(10 минут)
Первичное применение знаний (10 минут)
Подведение итогов урока (рефлексия
10 минут)Домашнее задание
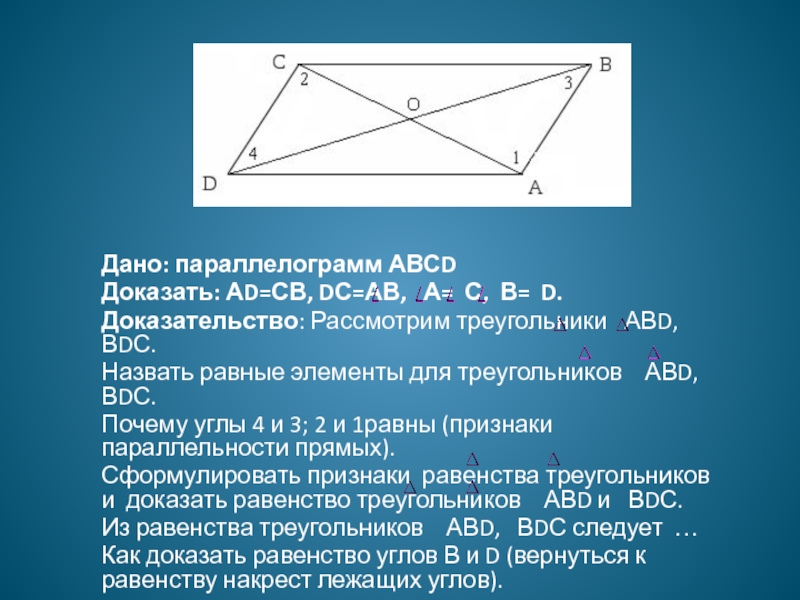
Слайд 7Дано: параллелограмм АВСD
Доказать: АD=СВ, DС=АВ, А= С, В= D.
Доказательство:
Рассмотрим треугольники АВD, ВDС.
Назвать равные элементы для треугольников
АВD, ВDС. Почему углы 4 и 3; 2 и 1равны (признаки параллельности прямых).
Сформулировать признаки равенства треугольников и доказать равенство треугольников АВD и ВDС.
Из равенства треугольников АВD, ВDС следует …
Как доказать равенство углов В и D (вернуться к равенству накрест лежащих углов).
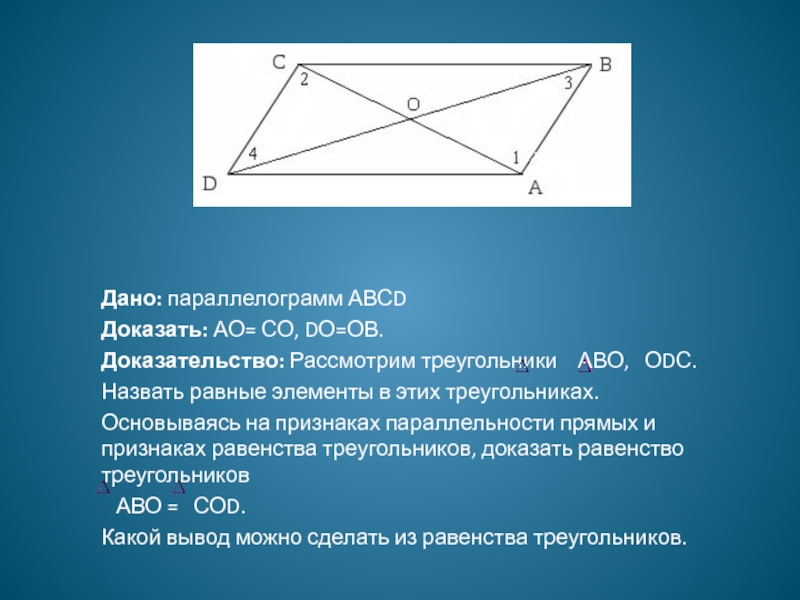
Слайд 9Дано: параллелограмм АВСD
Доказать: АО= СО, DО=ОВ.
Доказательство: Рассмотрим треугольники АВО,
ОDС.
Назвать равные элементы в этих треугольниках.
Основываясь на
признаках параллельности прямых и признаках равенства треугольников, доказать равенство треугольников АВО = СОD.
Какой вывод можно сделать из равенства треугольников.
Слайд 11Дано:
ABCD – параллелограмм
Доказать:
A + B
=
Доказательство: Пусть А = х и В
= у. Используем 1 свойство параллелограмма …
Сумма углов четырехугольника равна…
Составим уравнение…
Следовательно А + В=
Сформулируйте свойство параллелограмма. Сумма односторонних углов параллелограмма равна
Слайд 12
Дано:
ABCD – параллелограмм
АЕ – биссектриса угла А
Доказать:
АВЕ – равнобедренный
Доказательство:
Рассмотрите параллельные прямые АД и ВС и секущую АЕ.
Какова величина ВЕА, ЕАД, ВАЕ?
Обоснуйте свой ответ.
Вывод ( АВЕ – равнобедренный, так как ….. ).
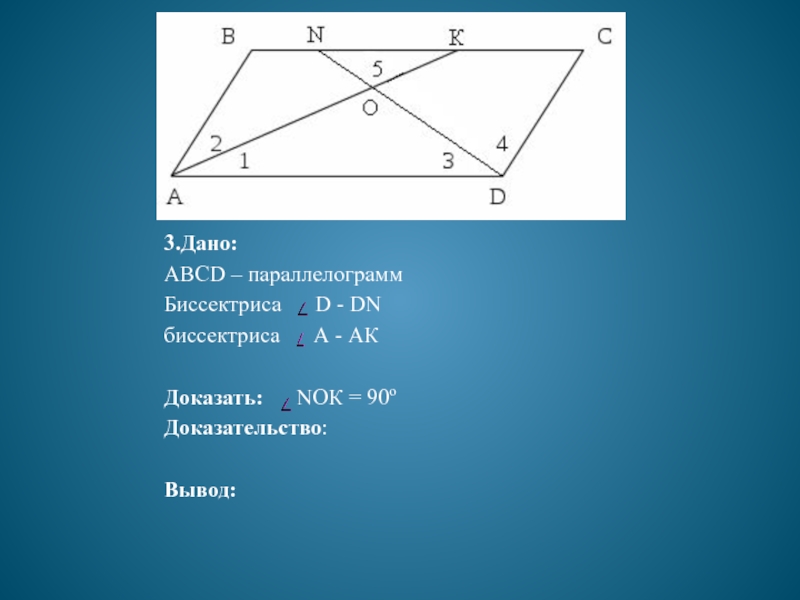
Слайд 133.Дано:
ABCD – параллелограмм
Биссектриса D - DN
биссектриса
А - АК
Доказать: NОК = 90о
Доказательство:
Вывод:
Слайд 14Математический диктант
Назвать фигуры, у которых диагонали равны
Назвать фигуры,
у которых противолежащие углы равны
Назвать фигуры, у которых диагонали
взаимно перпендикулярны Назвать фигуры, у которых противолежащие стороны равны
Назвать фигуры, у которых диагонали являются биссектрисами
Слайд 15Математический диктант
квадрат, прямоугольник
квадрат, прямоугольник, ромб, параллелограмм
квадрат, ромб
квадрат, прямоугольник, ромб, параллелограмм
квадрат, ромб
Слайд 16Критерии оценивания домашнего задания
Отметка «5»
Если выполнен 1 и
2 или 1 и 3 уровень домашнего задания;
В решении нет
математических ошибок, в логических рассуждениях и обосновании решения нет пробелов и ошибок;Геометрические задачи составлены без ошибок, отсутствуют излишние данные в условии, отсутствуют ошибки и недочеты в чертежах;
Кроссворд содержит не менее 20 понятий по теме «параллелограмм», составлен без ошибок и повторений.
Отметка «4»
Если выполнен 1 и 2 или 3 уровень домашнего задания, но обоснования шагов решения недостаточны;
Допущена одна ошибка или два-три недочета в чертежах, допущены недочеты при составлении геометрических задач;
Кроссворд содержит не менее 15 понятий по теме «параллелограмм», составлен без ошибок и повторений.
Отметка «3»
Если выполнен 1 и 2 уровень домашнего задания, но обоснования шагов решения недостаточны;
Кроссворд содержит не менее 10 понятий по теме «параллелограмм», составлен без ошибок и повторений.
Допущены более одной ошибки или более двух-трех недочетов в чертежах или при решении задач, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2»
Допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.