Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Установление соотношения между сторонами и углами прямоугольного треугольника
Содержание
- 1. Установление соотношения между сторонами и углами прямоугольного треугольника
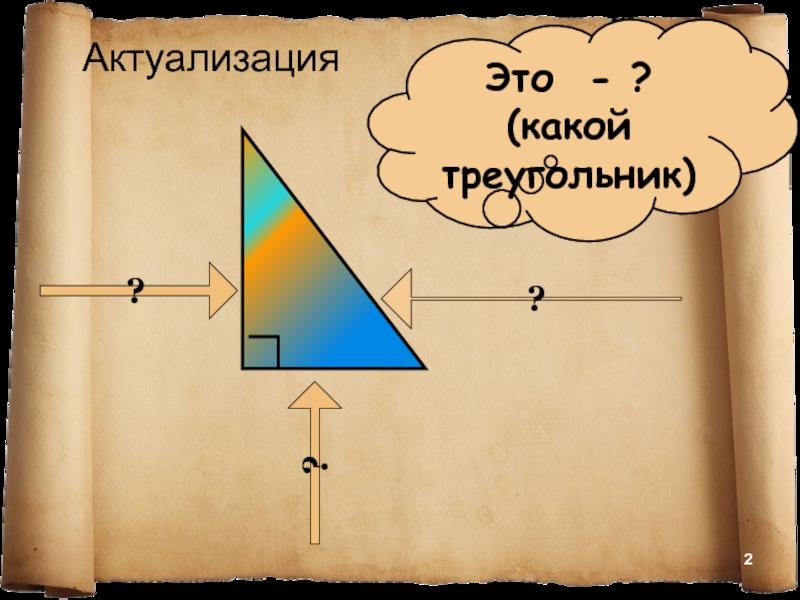
- 2. ???Это - ? (какой треугольник) Актуализация
- 3. Практическая работа «Установление соотношения между сторонами и
- 4. Теорема Пифагора*
- 5. РефлексияЧто нового вы узнали о прямоугольном треугольнике?На
- 6. 1. Указать прямоугольный треугольник2. Записать для него
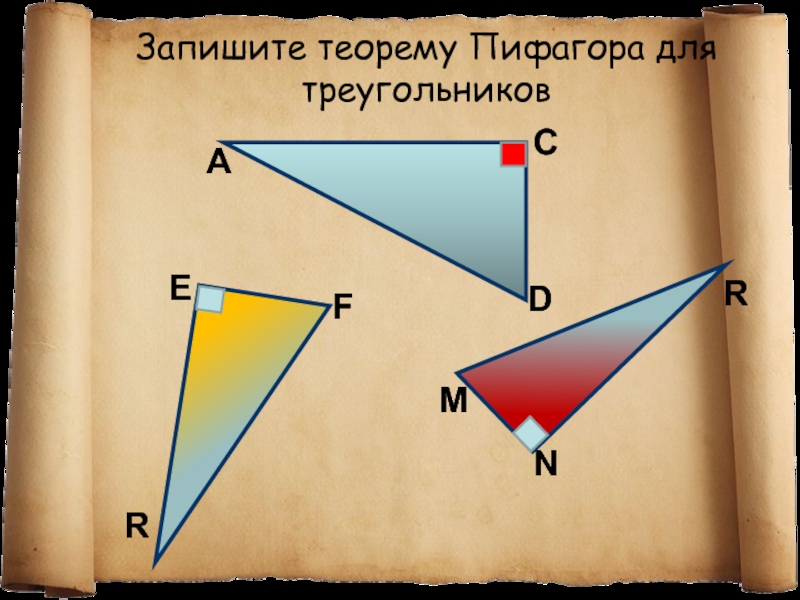
- 7. Запишите теорему Пифагора для треугольниковCDFERMRNA
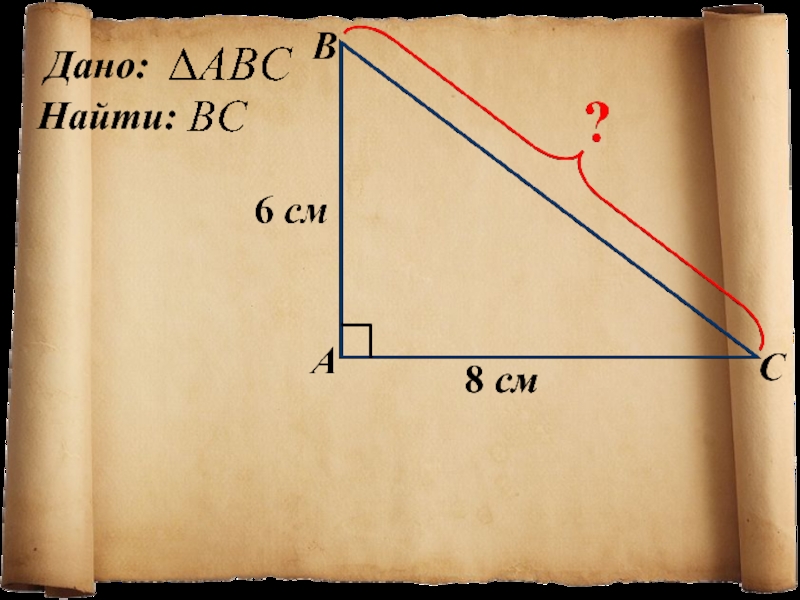
- 8. Найти:Дано:8 см
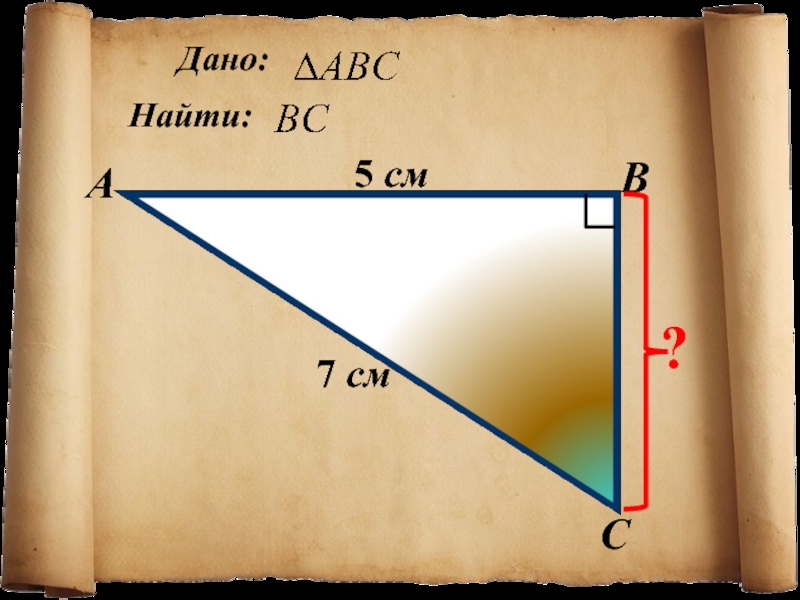
- 9. Дано:Найти:
- 10. (ок. 580 – 500 г. до н.э.)
- 11. Слайд 11
- 12. Древние репродукции доказательства теоремы Пифагора
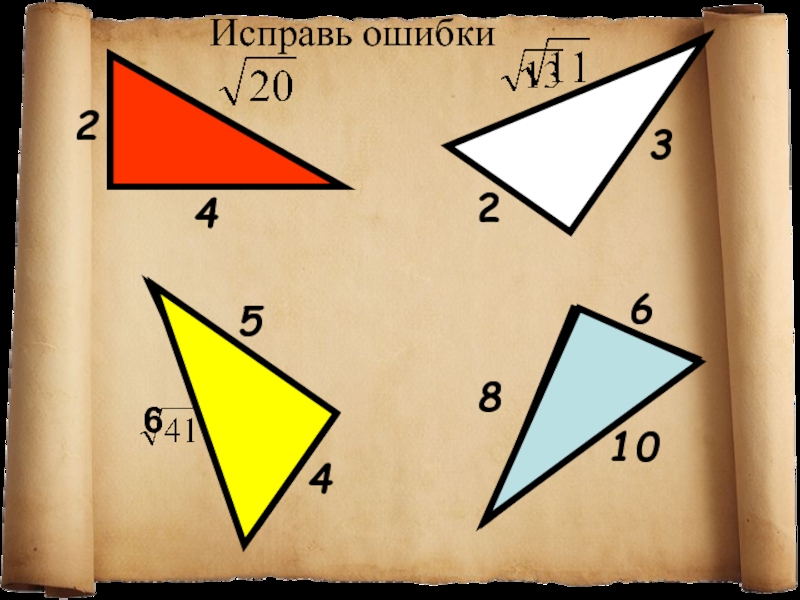
- 13. 6Исправь ошибки
- 14. Домашнее заданиеП 54, вопрос 7, стр 134№№483(а, в), 484(а, б)_ обязательно№ 513_ по желанию
- 15. Слайд 15
- 16. СертификатНастоящим подтверждается успешное усвоение учащимися 8 Г класса теоремы Пифагора в ходе урока геометрии*
- 17. Пребудет вечной истина, как скоро Ее познает
- 18. Пифагоровы тройкиПрямоугольные треугольники с целочисленными сторонами называют
- 19. Пифагоровы тройкиПифагоровы числа обладают рядом свойств Один
- 20. Скачать презентанцию
???Это - ? (какой треугольник) Актуализация
Слайды и текст этой презентации
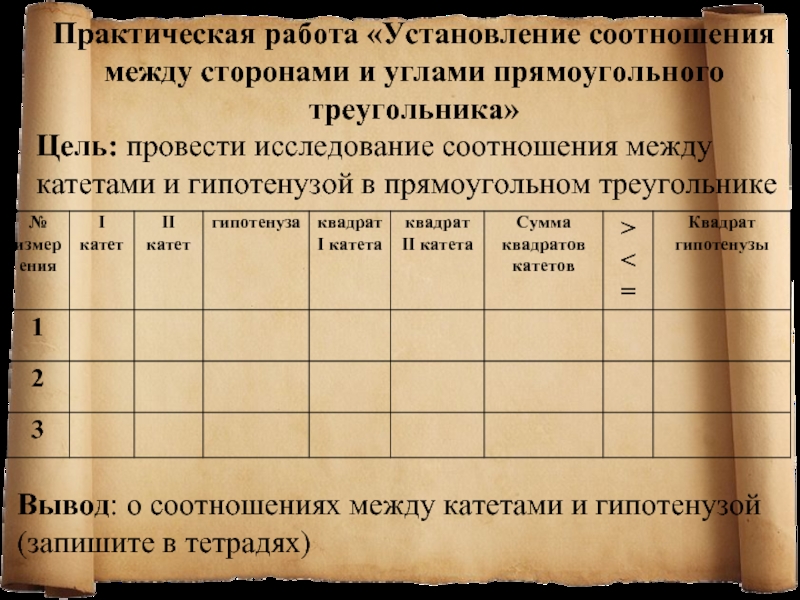
Слайд 3Практическая работа «Установление соотношения между сторонами и углами прямоугольного треугольника»
Цель:
провести исследование соотношения между катетами и гипотенузой в прямоугольном треугольнике
Вывод: о соотношениях между катетами и гипотенузой (запишите в тетрадях)
Слайд 5Рефлексия
Что нового вы узнали о прямоугольном треугольнике?
На какие свойства площадей
опирались при доказательстве теоремы Пифагора?
Какие ранее изученные формулы площади мы
использовали?Слайд 61. Указать прямоугольный треугольник
2. Записать для него теорему Пифагора
с2 = а2+b2
Подставить известные значения сторон.
Найти неизвестную сторону, произведя вычисления.
Алгоритм применения теоремы Пифагора
Слайд 16Сертификат
Настоящим подтверждается успешное усвоение учащимися 8 Г класса теоремы Пифагора
в ходе урока геометрии
*
Слайд 17Пребудет вечной истина, как скоро
Ее познает слабый человек!
И
ныне теорема Пифагора Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, свету вслед.
Они не в силах свету помешать ,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Слайд 18Пифагоровы тройки
Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки
целых чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника,
– пифагоровыми тройками.Слайд 19Пифагоровы тройки
Пифагоровы числа обладают рядом свойств
Один из «катетов»
должен быть кратным трём.
Один из «катетов» должен быть кратным
четырём.Одно из пифагоровых чисел должно быть кратно пяти.
Теги