Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Активные методы обучения на уроках математики"
Содержание
- 1. "Активные методы обучения на уроках математики"
- 2. Активные методы обучения - методы, стимулирующие познавательную деятельность
- 3. Что же такое АМО? АКТИВНЫЕ МЕТОДЫ
- 4. Активные методы обучения,
- 5. Для каждого этапа урока используются
- 6. Неизменным успехом пользуется у школьников конкурс "Художников",
- 7. Игра «Горячий стул» Ученик садится на
- 8. Математическое домино – состоит из 12-30 карточек
- 9. Игра «Теорема - пазл» Учащимся предлагается
- 10. Игра «Формула - пазл».(a + b)(a+b)(a+b)a +
- 11. Игра «Определение - пазл» (составить логическую цепочку)
- 12. Заметно повышают интерес учащихся математические кроссворды, ребусы.
- 13. Мозговой штурм (мозговая атака) широко применяемый способ
- 14. Пример использования приёма «Мозговой штурм» на
- 15. Приём «Синквейн» Приём «Синквейн» - это
- 16. Прием "Кластеры"Прием "Кластеры" используется как на стадии
- 17. Кластер по теме «Квадратные уравнения»Квадратные уравненияПриведённое
- 18. Прием «Ромашка» Делается цветок на каждом
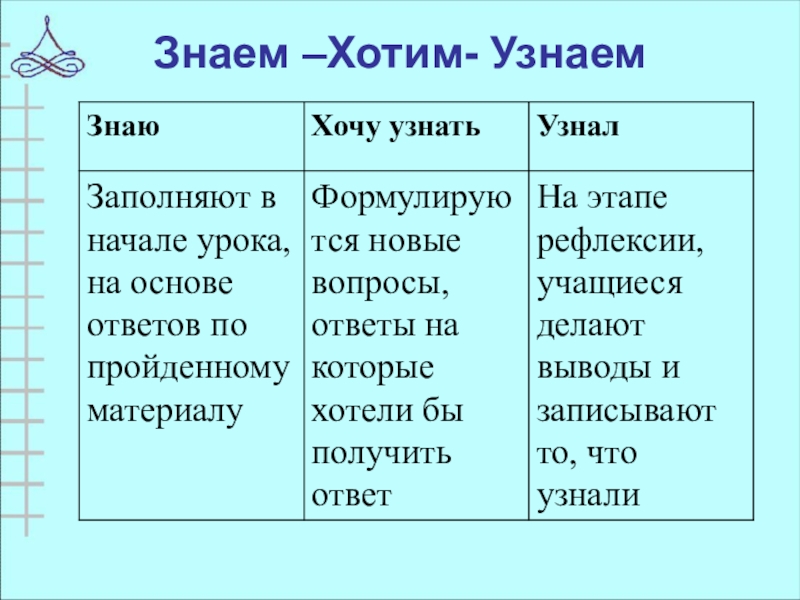
- 19. Знаем –Хотим- Узнаем
- 20. Метод рецензирования. В развитии творческой
- 21. Кейсовые технологии Кейсовые технологии получили
- 22. Тема: «Сложение и вычитание десятичных дробей»
- 23. Далее дается занимательная задача: «А
- 24. С давних времен разные растения,
- 25. Карточки с названиями деревьев расставить по алфавиту
- 26. Ключ: лиственница – смелость, сосна – верность,
- 27. Использование метода деловой игры.
- 28. Тема: «Проценты» (5 класс) Примерный
- 29. Слайд 29
- 30. Правила игры Чтобы приобрести товар, покупатели
- 31. Игра «Верю - Не верю». Например,
- 32. Игра «Самый, самый…» У учащихся на партах лежат
- 33. Эффективность АМО Как показали исследования немецких
- 34. Параллельно с обучением и воспитанием,
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Учитель математики филиала
МБОУ Луганской СОШ в с.Бобрик
Комаричского района
из опыта работы)
Слайд 2Активные методы обучения - методы, стимулирующие познавательную деятельность обучающихся.
Если верить некоторым источникам, активные методы и формы обучения
впервые появились еще в античности, где в гимназиях устраивались состязания между учениками, целью которых было получение знаний и умений. Однако в средневековой Европе сложилась схоластическая система обучения («учитель спрашивает, ученики отвечают»). В XX веке вместе с мощными шагами вперед таких наук как психология и педагогика начали развиваться и активные методы обучения.Слайд 3Что же такое АМО?
АКТИВНЫЕ МЕТОДЫ ОБУЧЕНИЯ – методы,
стимулирующие познавательную деятельность обучающихся.
АМО строятся:
в основном на
диалоге, предполагающем свободный обмен мнениями о путях разрешения той или иной проблемына практической направленности, игровом действие и творческом характере обучения;
интерактивности, разнообразных коммуникациях,
на использовании знаний и опыта обучающихся, групповой форме организации их работы,
деятельностном подходе к обучению, движении и рефлексии.
Слайд 4 Активные методы обучения, игровые методы –
очень гибкие методы, многие из них
можно использовать с разными возрастными группами и в разных условиях.Если привычной и желанной формой деятельности для ребенка является игра, значит надо использовать эту форму организации деятельности для обучения, объединив игру и учебно-воспитательный процесс, точнее, применив игровую форму организации деятельности обучающихся для достижения образовательных целей. Таким образом, мотивационный потенциал игры будет направлен на более эффективное освоение школьниками образовательной программы.
Слайд 5 Для каждого этапа урока используются свои активные методы,
позволяющие эффективно решать конкретные задачи этапа.
Каждый метод активным
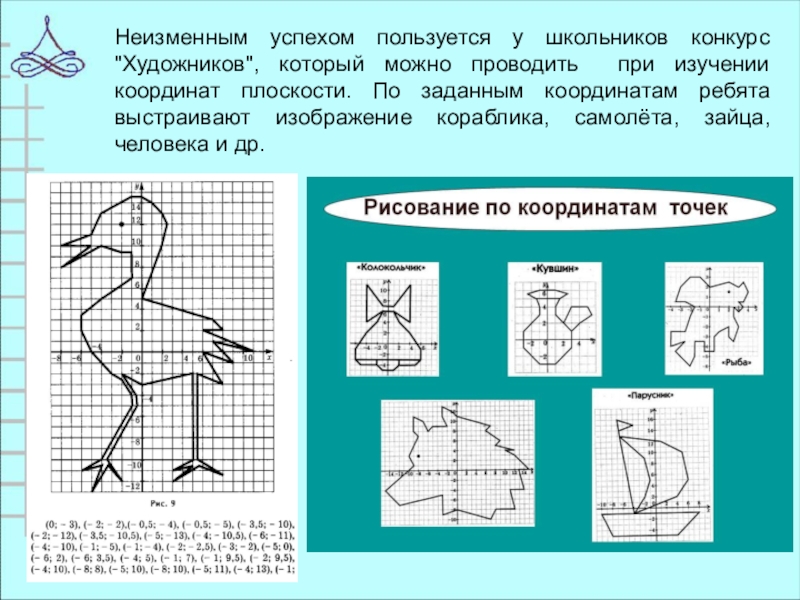
делает тот, кто его применяет.Слайд 6Неизменным успехом пользуется у школьников конкурс "Художников", который можно проводить
при изучении координат плоскости. По заданным координатам ребята выстраивают изображение
кораблика, самолёта, зайца, человека и др.Слайд 7Игра «Горячий стул»
Ученик садится на стул, а учащиеся
задают примеры для устного решения до тех пор, пока он
не собьется, затем его сменяет тот, кто предложил последний пример, игра продолжается. Побеждает тот, кто решил больше примеров.Слайд 8Математическое домино – состоит из 12-30 карточек каждая карточка разделена
чертой на две части – на одной записано задание, на
другой – ответ к другому заданию.Слайд 9Игра «Теорема - пазл»
Учащимся предлагается собрать теорему из
4 фрагментов. На одном содержится формулировка теорем, на другом –
чертеж к теореме, на третьем - что дано и что требуется доказать, на четвертом - доказательство.Слайд 10Игра «Формула - пазл».
(a + b)
(a+b)(a+b)
a + 2ab + b
a
- 2ab + b
Квадрат суммы двух выражений равен квадрату первого
выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения
Квадрат суммы двух выражений равен квадрату
первого выражения, минус удвоенное
произведение первого и второго выражений,
плюс квадрат второго выражения
a – b
(a - b)
Слайд 11Игра «Определение - пазл»
(составить логическую цепочку)
Тема «Треугольники».
Треугольник
называется
Если все три угла равны
Прямоугольный треугольник
Остроугольный треугольник
один прямой угол
если два
угла равныЕсли в треугольнике
треугольник тупоугольный
это треугольник, у которого
то треугольник равносторонний
равнобедренным
имеет все острые углы
один тупой угол, то
(Ответы: 1-11-6; 2-10; 3-9-5; 4-12; 7-13-8)
Слайд 13Мозговой штурм (мозговая атака)
широко применяемый способ продуцирования новых идей
для решения научных и практических проблем. Его цель — организация
коллективной мыслительной деятельности по поиску нетрадиционных путей решения проблем.Слайд 14Пример использования приёма «Мозговой штурм» на уроке алгебры в 8
классе по теме: «Преобразование выражений, содержащих квадратные корни»
Ситуация: Над вашей Компанией
нависла угроза банкротства. В случае невыполнения
следующего задания:
докажите, что выражения:
а) (5 ) + 3 ; б) ( – )( + )
в) ( + 2 ) – 4
являются натуральными числами
Компания будет объявлена банкротом.
Спасите Компанию.
Слайд 15Приём «Синквейн»
Приём «Синквейн» - это стихотворение, представляющее собой
синтез информации в лаконичной форме, что позволяет описывать суть понятия
или осуществлять рефлексию на основе полученных знаний.Для его написания существуют следующие правила:
Название – 1 существительное, описание – 2 прилагательных, действия – 3 глагола, чувство – фраза из 4 слов, повторение сути – синоним (1 слово)
Примеры синквейнов, составленных учениками:
Треугольник
Равнобедренный, равносторонний
Строится, является, называется
Сумма сторон треугольника – периметр
Призма Правильная, наклонная Рисовать, измерять, строить Мир, как через призму. Радуга
Слайд 16Прием "Кластеры"
Прием "Кластеры" используется как на стадии вызова, так и
на стадии рефлексии, т.е. может быть способом мотивации к размышлению
до изучения темы или формой систематизирования информации при подведении итогов. В зависимости от цели организуется индивидуальная или самостоятельная работа учащихся или коллективная – в виде общего совместного обсуждения. Например, составление кластера по теме «Квадратные уравнения»Слайд 17Кластер по теме
«Квадратные уравнения»
Квадратные
уравнения
Приведённое
квадратное
уравнение
Неприведённое
квадратное
уравнение
Х
– 3х + 1 = 0
Неполное
квадратное
уравнение
(b = 0)5х = 0
Неполное
квадратное
уравнение
4х + 5х + 1 = 0
Х – 3 = 0
Полное
квадратное
уравнение
Неполное
квадратное
уравнение (b=c= 0)
Неполное
квадратное
уравнение (c = 0)
3х – 2х = 0
Х + 3х + 2 = 0
0,2х – 2х = 0
3х – 5х + 2 = 0
Слайд 18Прием «Ромашка»
Делается цветок на каждом лепестке, которого содержится
пример или вопрос или указан термин, понятие. Каждый ученик отрывает
по одному лепестку и решает пример или отвечает на вопрос или дает определение термину.6,9 – 3, 8
8 + 4,4
1,2 * 5
4,8 : 0,8
10 – 3,6
2,5 + 4,2
3,2 * 0,3
2,4 : 3
десятичные
дроби
Слайд 20Метод рецензирования.
В развитии творческой активности учащихся большую роль
играет метод рецензирования.
Умение увидеть свою ошибку, указать ее
причину и исправить всегда приводит к возрастанию активности учащихся на уроке. Например: при объяснении нового материала решаю сама уравнение, а ученики прилежно списывают:(4х + 15) * 2 – 3 = 43;
8х + 30 – 3 = 43;
8х = 43 + 27 (умышленная ошибка), естественно при проверке ответ не сходится, среди учеников ажиотаж. Я говорю громко: «Найдите ошибку!».
В результате все решают устно самостоятельно и увлеченно.
Слайд 21Кейсовые технологии
Кейсовые технологии получили широкое применение в
образовательной среде. Эту методику успешно применяют в качестве тренинговой как
в высшей школе, так и в средней.Кейс - стади позволяет закрепить полученные на занятиях знания в конкретных игровых ситуациях, активизируют учебный процесс.
На уроках математики в средней школе эффективно применяются ситуации – иллюстрации и ситуации – упражнения.
Слайд 22
Тема: «Сложение и вычитание десятичных дробей»
Разминочные
упражнения.
Великий греческий математик Пифагор имел к числам
особенное отношение, присваивал каждому числу какой-либо символ, например, «5» - символ цвета, «6» - холода, «7» обозначало разум и здоровье, «8» - любовь и дружбу. Именно Пифагор разделил все числа на четные и нечетные. Слайд 23 Далее дается занимательная задача: «А сейчас вы попробуйте
повторить открытие, сделанное Пифагором. На доске записаны все нечетные числа
от 1 до 19 (1,3,5,7,9,11,13,15,17,19). Найдите сумму первых двух, потом первых трех, затем четырех и т.д. Полученные ответы запишите в строчку. Какое открытие сделал Пифагор (4,9,16,25,36,49,64,81,100!)?Слайд 24 С давних времен разные растения, деревья и кустарники
люди наделяли определенной символикой. Так, например, лавр символизирует славу, олива
– мир.После этого выполняются вычисления с определением соответствия чисел и растений. По совпадающим ответам выясняем, какие деревья символами каких качеств являются:
Слайд 26Ключ: лиственница – смелость, сосна – верность, рябина – благоразумие,
апельсин – щедрость, вишня – стойкость.
Оставшееся дерево (грецкий орех) символизирует
хитрость.Слайд 27
Использование метода деловой игры.
Игра в качестве средства
обучения и воспитания детей используется давно. В настоящее время деловая
игра используется в учебном процессе в качестве одного из методов активного обучения. В деловой игре обучение происходит в процессе совместной деятельности. При этом каждый ученик решает свою отдельную задачу в соответствии со своей ролью и функцией.Слайд 28Тема: «Проценты» (5 класс)
Примерный сценарий деловой игры: в
витрине магазина «Детский мир» повесили объявление; «Предпраздничная распродажа! Цены снижены
на 20%, 25%, 50%, 60%». Действующие лица: директор магазина (учитель), продавец (1 ученик), кассир (1 ученик), покупатели (остальные ученики в классе). На распродаже продаются мягкие игрушки (Мишка или Зайчик, Кот или Лев, Слоник или Бегемот, Дельфин или Обезьянка).Слайд 29 20%
25% 50% 60%
Старая
цена
Мишка Кот Слоник Дельфин
Зайчик Лев Бегемот Обезьянка
Новая
цена
100
400
450
800
Распродажа игрушек
Слайд 30Правила игры
Чтобы приобрести товар, покупатели решают задачи и
выясняют изменения в ценниках на товары. Продавцы контролируют ход игры,
при необходимости помогают в выборе товара. Кассиры убеждаются в правильности решения задач. Директор магазина осуществляет решение задач при наличии конфликтных ситуаций. Вся игровая деятельность происходит на фоне и в соответствии с дидактической моделью игры, включающей такие элементы, как игровую модель деятельности, систему оценивания.Слайд 31Игра «Верю - Не верю».
Например, на уроке математики
в 6 классе по теме «Рациональные числа» можно использовать такие
вопросы:-12 - число отрицательное? (да)
56 - число положительное?(да)
При сложении отрицательных чисел получается число положительное (нет)
-13+(-15) = 28 (нет)
-5 +(-24)= -29 (да)
Нуль больше любого отрицательного числа (да)
Из двух отрицательных чисел то больше, модуль которого больше (нет)
Из двух чисел то число больше, которое находится правее на координатной прямой(да)
Слайд 32Игра «Самый, самый…»
У учащихся на партах лежат карточки с целыми
числами от -10 до 10 (20 штук) в произвольном порядке.
По ходу урока учащимся предлагается следующее: - встаньте, чей модуль равен 7; - встаньте, чья сумма равна нулю (за одной партой); - встаньте, у кого числа одинаковых знаков; назовите сумму; - встаньте, чье число не является положительным; - для каждой парты: назовите расстояние между вами на координатной прямой; - для каждой парты: назовите количество целых чисел, расположенных между вами и т.п.Слайд 33Эффективность АМО
Как показали исследования немецких ученых, человек запоминает
только 10% того, что он читает, 20% того, что слышит,
30% того, что видит; 50-70% запоминается при участии в групповых дискуссиях, 80% - при самостоятельном обнаружении и формулировании проблем.И лишь когда обучающийся непосредственно участвует в реальной деятельности, в самостоятельной постановке проблем, выработке и принятии решения, формулировке выводов и прогнозов, он запоминает и усваивает материал на 90%. Близкие к приведенным данные были получены также американскими и российскими исследователями.
Слайд 34 Параллельно с обучением и воспитанием, применение АМО в
образовательном процессе обеспечивает становление и развитие у обучающихся универсальных навыков:
способность принимать
решения и умение решать проблемы,коммуникативные умения и качества,
умения ясно формулировать сообщения и четко ставить задачи,
умение выслушивать и принимать во внимание разные точки зрения и мнения других людей,
лидерские умения и качества,
умение работать в команде и др.