Аликвотные дроби

Содержание

1. Аликвотные дроби
2. Аликвотными дробями, называют дроби вида, 1/nгде числитель
3. Это нужно было для того:1. чтобы разделить
4. Дробей вида 1/nЕщё в древнем Египте у
5. Все дробные числа записывались в виде аликвотных
6. глаз «Хора» - единица для измерения ёмкостей
7. Такие дроби имели разные названия , но
8. Дроби в Древнем ЕгиптеЧасть папируса АхмесаЗадача «о хлебах» Разделить 7 хлебов между 8 людьми.РЕШЕНИЕ:
9. Складывать такие дроби было неудобно. Ведь в
10. Дроби вида 2/n и 2/(2n + 1)
11. Скажем, число 2/43 оказалось более сложно разложить
12. Разложить в виде разности двух аликвотных
13. Таким образом, при разработке данной темы, мы
14. Скачать презентанцию

Аликвотными дробями, называют дроби вида, 1/nгде числитель 1, а n – натуральное число.В переводе от латинского aliguot- "несколько'‘.Определение

Слайды и текст этой презентации

Слайд 1
Презентация по математике на тему:
«Аликвотные дроби».

Выполнила: учитель математики Попок Л.А.

г.

Ростов-на-Дону
2015г.

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №31

Презентация по математике на тему:«Аликвотные дроби». Выполнила: учитель математики Попок Л.А. г. Ростов-на-Дону2015г.Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа

Слайд 2Аликвотными дробями,
называют дроби вида, 1/n
где числитель 1, а n

– натуральное число.
В переводе от латинского aliguot- "несколько'‘.
Определение

Аликвотными дробями, называют дроби вида, 1/nгде числитель 1, а n – натуральное число.В переводе от латинского aliguot-

Слайд 3
Это нужно было для того:

1. чтобы разделить добычу после охоты,

ведь, нужно было знать, сколько частей составляет целое и кому

какая часть добычи станет принадлежать.

2. чтобы поделить основную меру объёма в Древнем Египте - «хекат».

1/2, 1/3, 1/4 - первые дроби, с которыми нас знакомит история. Причиной появления этих дробей являлась необходимость разбить единицу на доли.

Это нужно было для того:1. чтобы разделить добычу после охоты, ведь, нужно было знать, сколько частей составляет

Слайд 4Дробей вида 1/n
Ещё в древнем Египте у людей возникла потребность

записывать дроби как суммы долей.
У египтян и у вавилонян эти

дроби имели специальные обозначения.

1
2

Дробей вида 1/nЕщё в древнем Египте у людей возникла потребность записывать дроби как суммы долей.У египтян и

Слайд 5Все дробные числа записывались в виде
аликвотных (единичных) дробей:

8/15 = 1/3 + 1/5;

1/2 = 1/3 + 1/6,
1/4 = 1/5 + 1/20.

Все дробные числа записывались в виде аликвотных (единичных) дробей: 8/15 = 1/3 +

Слайд 6глаз «Хора» - единица для измерения ёмкостей и объемов.

Была представлена

в виде суммы аликвотных дробей:

63/64 = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64

Слайд 7Такие дроби имели разные названия , но все вместе назывались

аликвотами.
Вот несколько названий
Некоторые дошли до нас
1/100- процент
1/1000-промилли
1/288-скрупулус
1/24-семиунция
1/8-сескунция

Такие дроби имели разные названия , но все вместе назывались аликвотами.Вот несколько названийНекоторые дошли до нас1/100- процент1/1000-промилли1/288-скрупулус1/24-семиунция1/8-сескунция

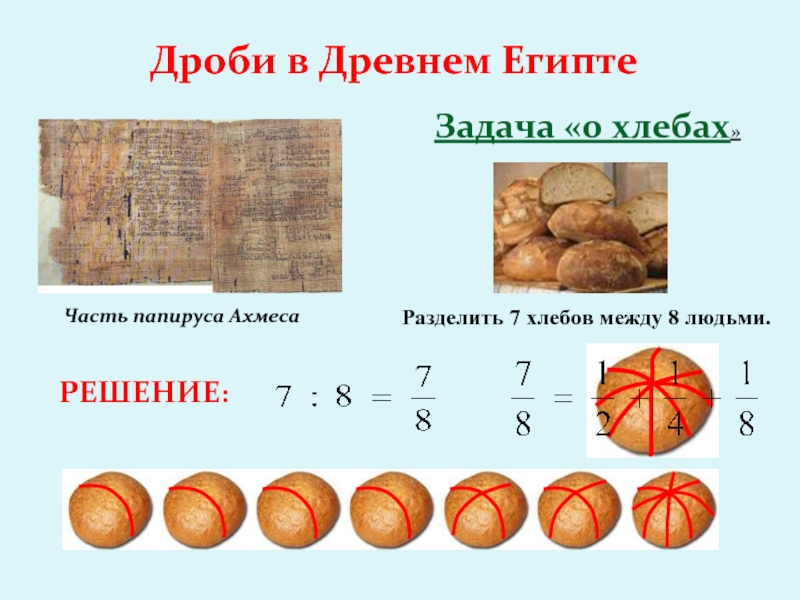
Слайд 8Дроби в Древнем Египте
Часть папируса Ахмеса
Задача «о хлебах»
Разделить 7

хлебов между 8 людьми.
РЕШЕНИЕ:

Слайд 9Складывать такие дроби было неудобно.
Ведь в оба слагаемых могут

входить одинаковые доли, и тогда при сложении появится дробь вида

2/n. А таких дробей египтяне не допускали.

Поэтому папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде сумм долей (в виде суммы двух, трёх или четырёх аликвот).

Складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении

Слайд 10Дроби вида 2/n и 2/(2n + 1) можно записать по

формулам:
2/n = 1/n + 1/n,
2/(2n + 1) = 1/(2n +1)

+ 1 /(2n + 1),

или
2/(2n + 1) = 1/(n +1) + 1 (2n + 1)(n +1).

Дроби вида 2/n и 2/(2n + 1) можно записать по формулам:2/n = 1/n + 1/n,2/(2n + 1)

Слайд 11Скажем, число 2/43 оказалось более сложно разложить на сумму 4

аликвотных дробей.
2/42 = 1/42 + 1/86 + 1/129 +

1/301

ДЕЙСТВИЯ С АЛИКВОТАМИ

Аликвоты можно складывать.
Аликвоты можно вычитать.
Аликвоты можно умножать.
Аликвоты можно делить.

Скажем, число 2/43 оказалось более сложно разложить на сумму 4 аликвотных дробей. 2/42 = 1/42 + 1/86

Слайд 12 Разложить в виде разности двух аликвотных дробей можно по

формуле:

1/n(n +1) = 1/n - 1/(n + 1)
Разложить в

виде суммы двух аликвотных дробей можно по формуле: 1/n = 1/(n +1) + 1/n(n + 1)

Разложить в виде разности двух аликвотных дробей можно по формуле: 1/n(n +1) = 1/n - 1/(n

Слайд 13Таким образом, при разработке данной темы, мы узнали, что первыми

дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием

аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Таким образом, аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек.

Заключение

Таким образом, при разработке данной темы, мы узнали, что первыми дробями, которыми оперировали люди, были аликвотные дроби.

Скачать презентацию

Теги

дроби

Разделы презентаций

Аликвотные дроби

Содержание

Слайды и текст этой презентации

Слайд 1
Презентация по математике на тему:
«Аликвотные дроби».

Выполнила: учитель математики Попок Л.А.

г.

Ростов-на-Дону
2015г.

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №31

Слайд 2Аликвотными дробями,
называют дроби вида, 1/n
где числитель 1, а n

– натуральное число.
В переводе от латинского aliguot- "несколько'‘.
Определение

Слайд 3
Это нужно было для того:

1. чтобы разделить добычу после охоты,

ведь, нужно было знать, сколько частей составляет целое и кому

Слайд 4Дробей вида 1/n
Ещё в древнем Египте у людей возникла потребность

записывать дроби как суммы долей.
У египтян и у вавилонян эти

Слайд 5Все дробные числа записывались в виде
аликвотных (единичных) дробей:

8/15 = 1/3 + 1/5;

Слайд 6глаз «Хора» - единица для измерения ёмкостей и объемов.

Была представлена

в виде суммы аликвотных дробей:

Слайд 7Такие дроби имели разные названия , но все вместе назывались

аликвотами.
Вот несколько названий
Некоторые дошли до нас
1/100- процент
1/1000-промилли
1/288-скрупулус
1/24-семиунция
1/8-сескунция

Слайд 8Дроби в Древнем Египте
Часть папируса Ахмеса
Задача «о хлебах»
Разделить 7

хлебов между 8 людьми.
РЕШЕНИЕ:

Слайд 9Складывать такие дроби было неудобно.
Ведь в оба слагаемых могут

входить одинаковые доли, и тогда при сложении появится дробь вида

Слайд 10Дроби вида 2/n и 2/(2n + 1) можно записать по

формулам:
2/n = 1/n + 1/n,
2/(2n + 1) = 1/(2n +1)

Слайд 11Скажем, число 2/43 оказалось более сложно разложить на сумму 4

аликвотных дробей.
2/42 = 1/42 + 1/86 + 1/129 +

Слайд 12 Разложить в виде разности двух аликвотных дробей можно по

формуле:

1/n(n +1) = 1/n - 1/(n + 1)
Разложить в

Слайд 13Таким образом, при разработке данной темы, мы узнали, что первыми

дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Аликвотные дроби

Содержание

Слайды и текст этой презентации

Слайд 1Презентация по математике на тему:«Аликвотные дроби». Выполнила: учитель математики Попок Л.А. г.

Ростов-на-Дону2015г.Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №31

Слайд 2Аликвотными дробями, называют дроби вида, 1/nгде числитель 1, а n

– натуральное число.В переводе от латинского aliguot- "несколько'‘.Определение

Слайд 3Это нужно было для того:1. чтобы разделить добычу после охоты,

ведь, нужно было знать, сколько частей составляет целое и кому

Слайд 4Дробей вида 1/nЕщё в древнем Египте у людей возникла потребность

записывать дроби как суммы долей.У египтян и у вавилонян эти

Слайд 5Все дробные числа записывались в виде аликвотных (единичных) дробей:

8/15 = 1/3 + 1/5;

Слайд 6глаз «Хора» - единица для измерения ёмкостей и объемов.Была представлена

в виде суммы аликвотных дробей:

Слайд 7Такие дроби имели разные названия , но все вместе назывались

аликвотами.Вот несколько названийНекоторые дошли до нас1/100- процент1/1000-промилли1/288-скрупулус1/24-семиунция1/8-сескунция

Слайд 8Дроби в Древнем ЕгиптеЧасть папируса АхмесаЗадача «о хлебах» Разделить 7

хлебов между 8 людьми.РЕШЕНИЕ:

Слайд 9Складывать такие дроби было неудобно. Ведь в оба слагаемых могут

входить одинаковые доли, и тогда при сложении появится дробь вида

Слайд 10Дроби вида 2/n и 2/(2n + 1) можно записать по

формулам:2/n = 1/n + 1/n,2/(2n + 1) = 1/(2n +1)

Слайд 11Скажем, число 2/43 оказалось более сложно разложить на сумму 4

аликвотных дробей. 2/42 = 1/42 + 1/86 + 1/129 +

Слайд 12 Разложить в виде разности двух аликвотных дробей можно по

формуле: 1/n(n +1) = 1/n - 1/(n + 1)Разложить в

Слайд 13Таким образом, при разработке данной темы, мы узнали, что первыми

дробями, которыми оперировали люди, были аликвотные дроби. Задачи с использованием

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1
Презентация по математике на тему:
«Аликвотные дроби».

Выполнила: учитель математики Попок Л.А.

г.

Ростов-на-Дону
2015г.

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №31

Слайд 2Аликвотными дробями,
называют дроби вида, 1/n
где числитель 1, а n

– натуральное число.
В переводе от латинского aliguot- "несколько'‘.
Определение

Слайд 3
Это нужно было для того:

1. чтобы разделить добычу после охоты,

Слайд 4Дробей вида 1/n
Ещё в древнем Египте у людей возникла потребность

записывать дроби как суммы долей.
У египтян и у вавилонян эти

Слайд 5Все дробные числа записывались в виде
аликвотных (единичных) дробей:

Слайд 6глаз «Хора» - единица для измерения ёмкостей и объемов.

Была представлена

аликвотами.
Вот несколько названий
Некоторые дошли до нас
1/100- процент
1/1000-промилли
1/288-скрупулус
1/24-семиунция
1/8-сескунция

Слайд 8Дроби в Древнем Египте
Часть папируса Ахмеса
Задача «о хлебах»
Разделить 7

хлебов между 8 людьми.
РЕШЕНИЕ:

Слайд 9Складывать такие дроби было неудобно.
Ведь в оба слагаемых могут

формулам:
2/n = 1/n + 1/n,
2/(2n + 1) = 1/(2n +1)

аликвотных дробей.
2/42 = 1/42 + 1/86 + 1/129 +

формуле:

1/n(n +1) = 1/n - 1/(n + 1)
Разложить в

дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием