Свойства параллельных прямых

Содержание

1. Свойства параллельных прямых
2. Теоретический тест (с последующей самопроверкой)1. Выпишите
3. 4. Указать следствия аксиомы параллельных прямых:а) Если
4. Теоретический тестОтветы:1.Следует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;2. а;3.б;4.б,в,е,ж;
5. Задача 1.Доказать: AB||CDИзучение нового материалаЗадача 2.Дано: AB||CDНайти: ∠EKCРешите задачи:
6. Решение этих задач приводит к выводу:Если две
7. Составим таблицу.
8. Вывод Теорема, обратная данной, называется такая теорема,
9. Закрепление изученного материалаРешение задач по готовым чертежам:
10. Закрепление изученного материалаРешение задач по готовым чертежам:
11. Домашнее задание
12. Скачать презентанцию

Теоретический тест (с последующей самопроверкой)1. Выпишите лишние слова в скобках: Аксиома – это (очевидные, принятые, исходные) положения геометрии, не требующие (объяснений, доказательств, обоснований).2. Выбрать окончание формулировки аксиомы параллельных прямых:

Главная
Математика
Свойства параллельных прямых

Слайды и текст этой презентации

Слайд 1ПРЕЗЕНТАЦИЯ К УРОКУ ПО ГЕОМЕТРИИ НА ТЕМУ: СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

Слайд 2Теоретический тест (с последующей самопроверкой)
1. Выпишите лишние слова в скобках:

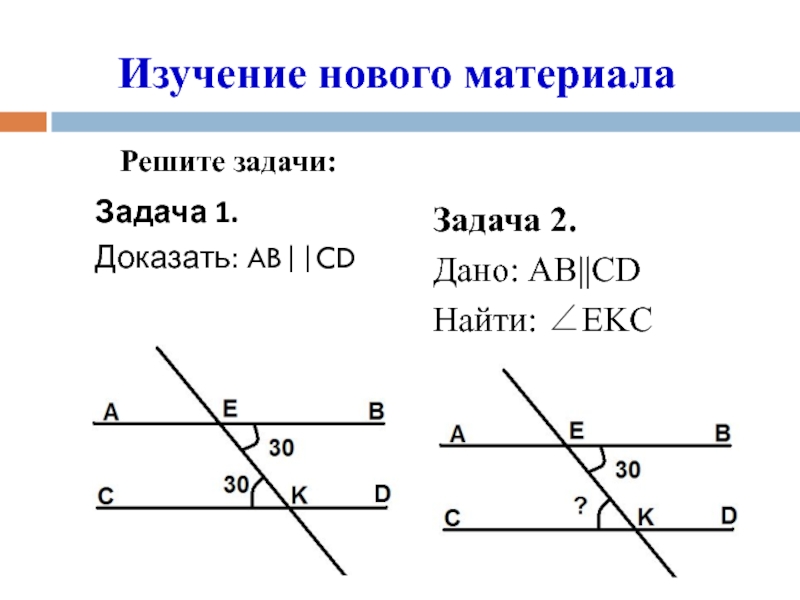
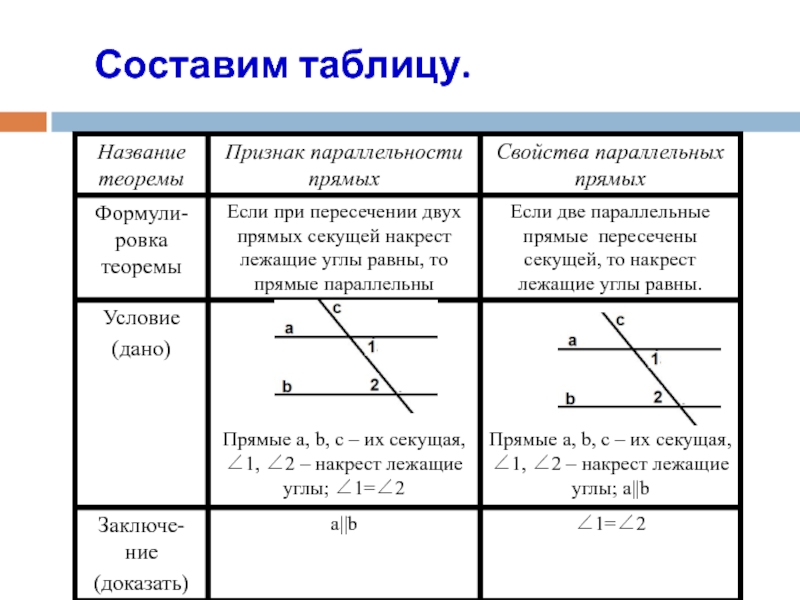
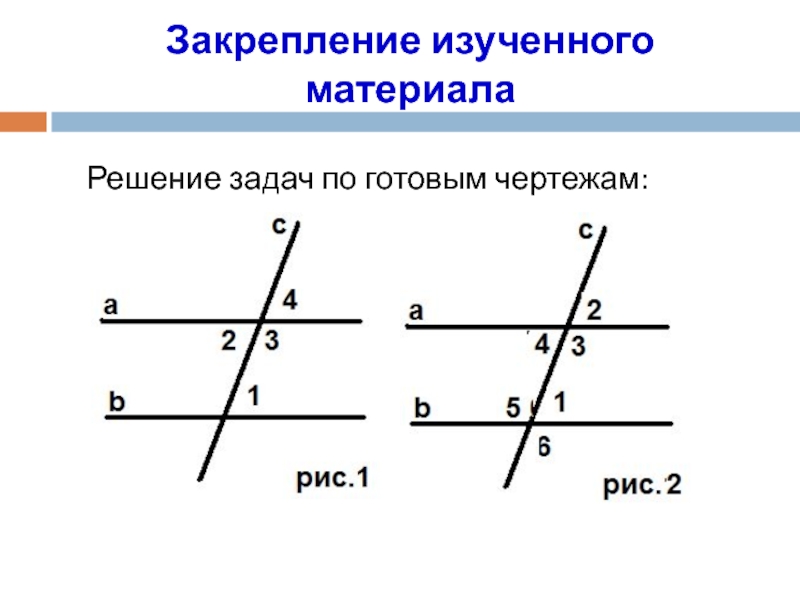
Аксиома – это (очевидные, принятые, исходные) положения геометрии, не

требующие (объяснений, доказательств, обоснований).
2. Выбрать окончание формулировки аксиомы параллельных прямых: Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая параллельная данной;
б) всегда проходит прямая параллельная данной;
в) только одна прямая, не пресекающаяся с данной.
3. Указать правильный ответ на вопрос:
Если через точку, лежащую вне прямой, проведено несколько прямых, то сколько из них пересекаются с исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку;
б) Все, кроме параллельной прямой;
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.

Теоретический тест (с последующей самопроверкой)1. Выпишите лишние слова в скобках: Аксиома – это (очевидные, принятые,

Слайд 3
4. Указать следствия аксиомы параллельных прямых:
а) Если отрезок или луч,

пересекает одну из параллельных прямых, то он и пересекает другую;
б)

Если две прямые параллельны третьей прямой, то они параллельны друг другу;
в) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
г) Если три прямые параллельны, то любые две из них параллельны друг другу;
д) Если две прямые не параллельные третьей прямой, то они не параллельны между собой;
е) Если прямая пересекает одну из двух параллельных прямых, то она не может и пересекать прямую;
ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.

4. Указать следствия аксиомы параллельных прямых:а) Если отрезок или луч, пересекает одну из параллельных прямых, то он

Слайд 4Теоретический тест
Ответы:
1.Следует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;
2. а;
3.б;
4.б,в,е,ж;

Слайд 5
Задача 1.
Доказать: AB||CD

Изучение нового материала
Задача 2.
Дано: AB||CD
Найти: ∠EKC

Решите задачи:

Слайд 6Решение этих задач приводит к выводу:
Если две параллельные прямые пересечены

третьей, то накрест лежащие углы равны.
Это свойство накрест лежащих углов.

Решение этих задач приводит к выводу:Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны.Это свойство

Слайд 7Составим таблицу.

Слайд 8Вывод
Теорема, обратная данной, называется такая теорема, в которой условие

является заключение данной теоремы, в заключение – условие данной теоремы.

Вывод Теорема, обратная данной, называется такая теорема, в которой условие является заключение данной теоремы, в заключение –

Слайд 9Закрепление изученного материала
Решение задач по готовым чертежам:

Слайд 10Закрепление изученного материала
Решение задач по готовым чертежам:

Слайд 11Домашнее задание

Скачать презентацию

Разделы презентаций

Свойства параллельных прямых

Содержание

Слайды и текст этой презентации

Слайд 1ПРЕЗЕНТАЦИЯ К УРОКУ ПО ГЕОМЕТРИИ НА ТЕМУ: СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

Слайд 2Теоретический тест (с последующей самопроверкой)
1. Выпишите лишние слова в скобках:

Аксиома – это (очевидные, принятые, исходные) положения геометрии, не

Слайд 3
4. Указать следствия аксиомы параллельных прямых:
а) Если отрезок или луч,

пересекает одну из параллельных прямых, то он и пересекает другую;
б)

Слайд 4Теоретический тест
Ответы:
1.Следует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;
2. а;
3.б;
4.б,в,е,ж;

Слайд 5
Задача 1.
Доказать: AB||CD

Изучение нового материала
Задача 2.
Дано: AB||CD
Найти: ∠EKC

Решите задачи:

Слайд 6Решение этих задач приводит к выводу:
Если две параллельные прямые пересечены

третьей, то накрест лежащие углы равны.
Это свойство накрест лежащих углов.

Слайд 7Составим таблицу.

Слайд 8Вывод
Теорема, обратная данной, называется такая теорема, в которой условие

является заключение данной теоремы, в заключение – условие данной теоремы.

Слайд 9Закрепление изученного материала
Решение задач по готовым чертежам:

Слайд 10Закрепление изученного материала
Решение задач по готовым чертежам:

Слайд 11Домашнее задание

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Свойства параллельных прямых

Содержание

Слайды и текст этой презентации

Слайд 1ПРЕЗЕНТАЦИЯ К УРОКУ ПО ГЕОМЕТРИИ НА ТЕМУ: СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

Слайд 2Теоретический тест (с последующей самопроверкой)1. Выпишите лишние слова в скобках:

Аксиома – это (очевидные, принятые, исходные) положения геометрии, не

Слайд 34. Указать следствия аксиомы параллельных прямых:а) Если отрезок или луч,

пересекает одну из параллельных прямых, то он и пересекает другую;б)

Слайд 4Теоретический тестОтветы:1.Следует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;2. а;3.б;4.б,в,е,ж;

Слайд 5 Задача 1.Доказать: AB||CDИзучение нового материалаЗадача 2.Дано: AB||CDНайти: ∠EKCРешите задачи:

Слайд 6Решение этих задач приводит к выводу:Если две параллельные прямые пересечены

третьей, то накрест лежащие углы равны.Это свойство накрест лежащих углов.

Слайд 7Составим таблицу.

Слайд 8Вывод Теорема, обратная данной, называется такая теорема, в которой условие

является заключение данной теоремы, в заключение – условие данной теоремы.

Слайд 9Закрепление изученного материалаРешение задач по готовым чертежам:

Слайд 10Закрепление изученного материалаРешение задач по готовым чертежам:

Слайд 11Домашнее задание

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 2Теоретический тест (с последующей самопроверкой)
1. Выпишите лишние слова в скобках:

Слайд 3
4. Указать следствия аксиомы параллельных прямых:
а) Если отрезок или луч,

пересекает одну из параллельных прямых, то он и пересекает другую;
б)

Слайд 4Теоретический тест
Ответы:
1.Следует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;
2. а;
3.б;
4.б,в,е,ж;

Слайд 5
Задача 1.
Доказать: AB||CD

Изучение нового материала
Задача 2.
Дано: AB||CD
Найти: ∠EKC

Решите задачи:

Слайд 6Решение этих задач приводит к выводу:
Если две параллельные прямые пересечены

третьей, то накрест лежащие углы равны.
Это свойство накрест лежащих углов.

Слайд 8Вывод
Теорема, обратная данной, называется такая теорема, в которой условие

Слайд 9Закрепление изученного материала
Решение задач по готовым чертежам:

Слайд 10Закрепление изученного материала
Решение задач по готовым чертежам: