Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок- презентация " Методы решения логарифмических уравнений"
Содержание
- 1. Урок- презентация " Методы решения логарифмических уравнений"
- 2. повторить определение логарифма; закрепить основные свойства
- 3. 1. Логарифмом
- 4. Разминка
- 5. Установите соответствие
- 6. Логарифм и ОДЗLoga b=Х ах =bb?a?Логарифм и ОДЗВМЕСТЕтрудятсявезде!
- 7. Методы решения
- 8. Метод решения хорош, если с
- 9. 1Решить уравнение, выбрав метод решения Проверить найденные
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. X=24X=10X=-10 и X=10log2x+4log4x=12X=16x=64xlgx=100x;
- 15. Проблема? Цель?
- 16. Первичное закрепление
- 17. Самостоятельная работаРешите уравнения методом логарифмированияxlgx=x100; x0,5lgx=0,01x2; X2log3x=3log33x
- 18. xlgx=x100; 1)ОДЗ: х>02) lgxlgx=lgx100;lg2x = 100lgxlg2x -
- 19. xlоg5x=x10;1)ОДЗ: х>02) Т. к. обе части уравнения
- 20. ДЖОН НЕПЕР (1550-1617) Шотландский математик –
- 21. н о
- 22. Спасибо за урок!
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Решение логарифмических уравнений
ПРЕПОДАВАТЕЛЬ МАТЕМАТИКИ:
Александрина Людмила Владимировна
ГБПОУ ЯНАО «Муравленковский колледж»
г. Муравленко
Слайд 2 повторить определение логарифма;
закрепить основные свойства логарифмов;
- способствовать
формированию умения применять свойства логарифмов при
решении уравнений;- развивать математическое мышление; технику
вычисления; умение логически мыслить
и рационально работать;
- воспитание познавательной активности, чувства
ответственности, уважения друг к другу.
Цели урока:
Слайд 3 1. Логарифмом числа b
по …………… а
называется ……………..
степени, в которуюнужно……………. основание а, чтобы
получить число b.
2. Основание и число, стоящее под знаком
логарифма, должны быть………….
3. Если основание а =….., то такой логарифм
называется десятичным и обозначается lg b.
основанию
показатель
возвести
положительными
10
Продолжи предложение.....
Слайд 8
Метод решения хорош, если с самого начала мы
можем предвидеть – и в последствии подтвердить это, что, следуя
нашему методу, мы достигли цели.Лейбниц
Слайд 91
Решить уравнение, выбрав метод решения
Проверить найденные корни непосредственной
подстановкой в исходное уравнение
2
Найти область
допустимых значений (ОДЗ) переменнойРешить уравнение, выбрав метод решения
Выяснить, удовлетворяют ли корни решённого уравнения ОДЗ
3
Заменить уравнение равносильным уравнением или равносильной системой
Пути решения уравнений
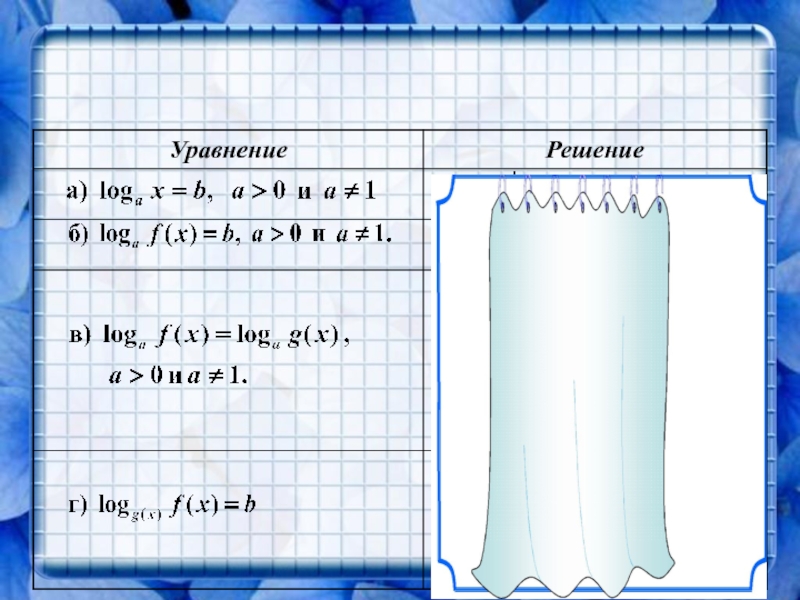
Слайд 15Проблема?
Цель?
xlgx=100x;
ОДЗ: х > 0
2) Т.
к. обе части уравнения положительны, то прологарифмируем их по основанию 10, получимlgxlgx=lg(100x);
lgx·lgx=lg(100х)
lg2x = lg100 + lgх
lg2x – lgх- 2=0
х =100, х=0,1
Ответ: х =100, х =0,1
Слайд 16Первичное закрепление
Xlgx+2 = 1000
1)ОДЗ: Х>0
2) Т.
к. обе части уравнения положительны, то логарифмируя их по основанию 10, получим:lgxlgx+2 = lg1000
( lgx+2)·lgx=lg1000
lg2x+ 2lgx- 3=0
lgx=y
у2 + 2у- 3=0
y=- 3, у=1.
lgx=- 3, x=10-3=0,001;
lgx=1, x=10
Ответ: 0,001; 10.
Слайд 17Самостоятельная работа
Решите уравнения методом логарифмирования
xlgx=x100;
x0,5lgx=0,01x2;
X2log3x=3log33x
Слайд 18
xlgx=x100;
1)ОДЗ: х>0
2) lgxlgx=lgx100;
lg2x = 100lgx
lg2x - 100lgx =0
lgx(lgx –
100) =0
lgx =0 или
lgx = 100
х =1 или
х =10100Ответ: х=1, х=10100
x0,5lgx=0,01x2;
1)ОДЗ: х>0
2) lgx0,5lgx=lg0,01x2;
0,5lgxlgx – (-2+2lgx)=0
0,5lg2x - 2lgx+2=0
lg2x - 4lgx +4 =0
(lgx -2)2=0
lgx =2
х=100
Ответ: х=100
X2log3x=3log33x
1)ОДЗ:х>0
2) log3X2log3x=log33log33x
2log3x·log3x=log3(3x)·log33
2log32x = 1+log3x
2log32x -1-log3x=0
X=10 или х=3-0,5
Х=√3/3
Ответ: х=10,
Х=√3/3
Самопроверка
Слайд 19xlоg5x=x10;
1)ОДЗ: х>0
2) Т. к. обе части уравнения положительны, то
прологарифмируя их
по основанию 5, получим
lоg5xlоg5x=lоg5x10;lоg25х = 10lоg5x
lоg25х -10lоg5x =0
lоg5x(lоg5x -10) =0
Lоg5x =0 или lоg5x = 10
х =1 или х = 5 10
Ответ: х =1 или х = 5 10
Слайд 20ДЖОН НЕПЕР
(1550-1617)
Шотландский математик –
изобретатель логарифмов.
В 1590-х годах пришел к идее
логарифмических вычислений
и составил первые таблицы
логарифмов, однако свой знаменитый
“Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
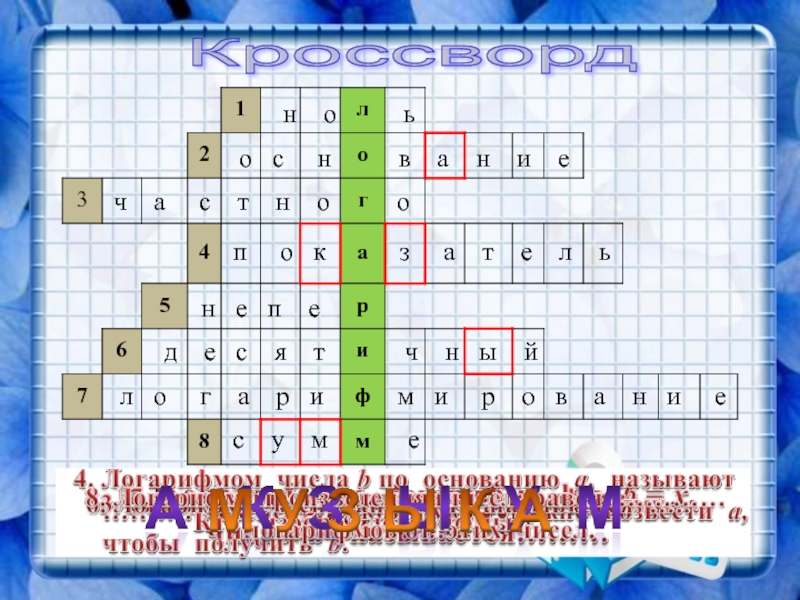
Слайд 21н о ь
ч а
с т н о
ос у м е
о с н в а н и е
п о к з а т е л ь
н е п е
д е с я т ч н ы й
л о г а р и м и р о в а н и е
Кроссворд













 " alt="Проблема? Цель? xlgx=100x;ОДЗ: х">
" alt="Проблема? Цель? xlgx=100x;ОДЗ: х">

 02) lgxlgx=lgx100;lg2x = 100lgxlg2x - 100lgx =0lgx(lgx – 100)" alt="xlgx=x100; 1)ОДЗ: х>02) lgxlgx=lgx100;lg2x = 100lgxlg2x - 100lgx =0lgx(lgx – 100) =0lgx =0 или lgx = 100х">
02) lgxlgx=lgx100;lg2x = 100lgxlg2x - 100lgx =0lgx(lgx – 100)" alt="xlgx=x100; 1)ОДЗ: х>02) lgxlgx=lgx100;lg2x = 100lgxlg2x - 100lgx =0lgx(lgx – 100) =0lgx =0 или lgx = 100х"> 02) Т. к. обе части уравнения положительны, то прологарифмируя их" alt="xlоg5x=x10;1)ОДЗ: х>02) Т. к. обе части уравнения положительны, то прологарифмируя их по основанию 5, получим">
02) Т. к. обе части уравнения положительны, то прологарифмируя их" alt="xlоg5x=x10;1)ОДЗ: х>02) Т. к. обе части уравнения положительны, то прологарифмируя их по основанию 5, получим">