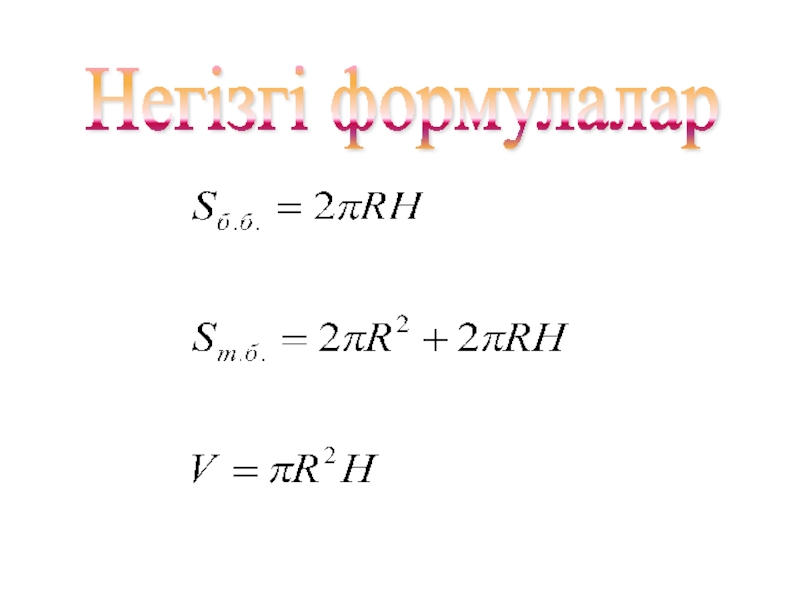Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Айналу денелері
Содержание
- 1. Айналу денелері
- 2. Қайталау.Қандай фигураны шеңбер деп атаймыз?
- 3. Қандай фигураны дөңгелек деп атаймыз?
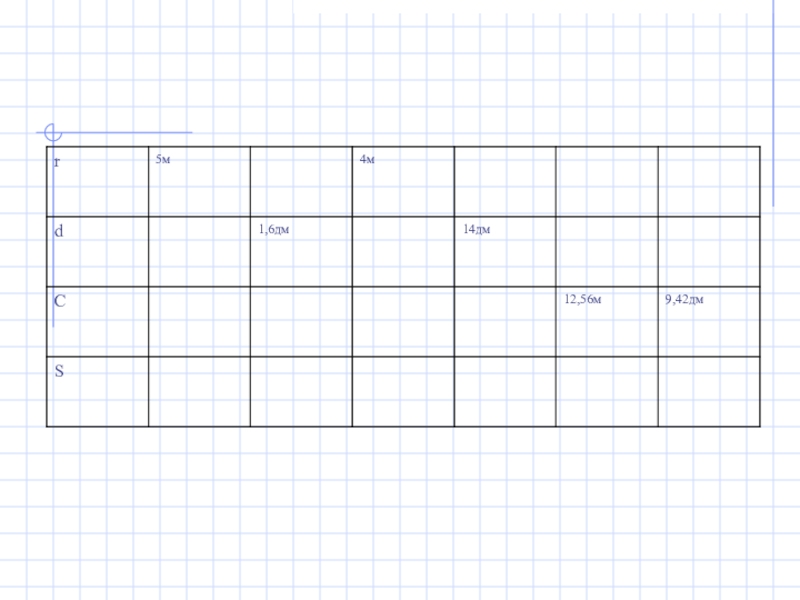
- 4. Шеңбердің ұзындығын табатын формуланы жазыңыз.Дөңгелектің ауданын табатын формуланы жазыңыз.
- 5. Слайд 5
- 6. .
- 7. Слайд 7
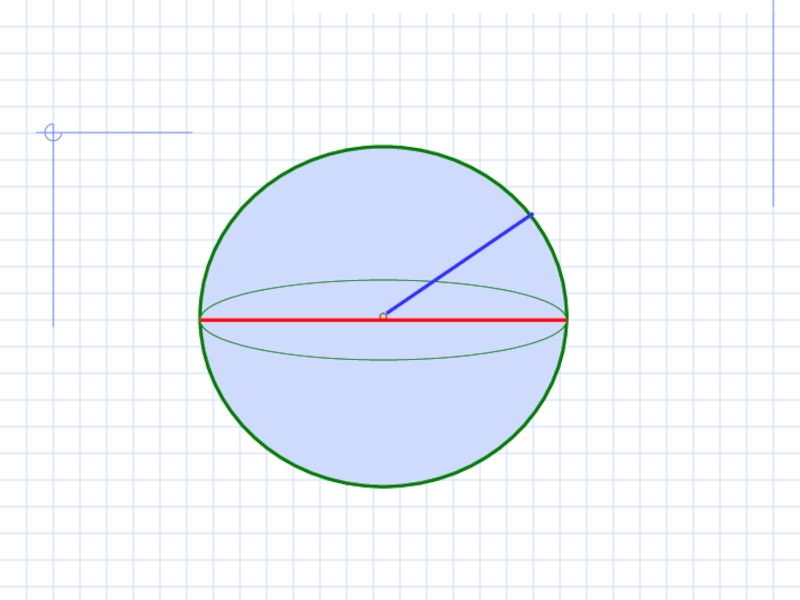
- 8. Шар — сферамен шектелген дене.Сфера- берілген нүктедең берілген қашықтағы кеңістік нүктелерінің геометриялық орны. Шардың беті –сфера.
- 9. Слайд 9
- 10. «Сфера» - грек сөзінің латын формасынан «сфайра» - доп.
- 11. Цилиндр
- 12. Цилиндр деп тік төртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын денені атайды.Цилиндр
- 13. Цилиндрдің элементтері Дөңгелектер цилиндрдің табандары деп аталады,
- 14. Цилиндрдің табандары тең. Цилиндрдің табандары параллель жазықтықтарда жатады.Цилиндрдің элементтерінің қасиеттері Цилиндрдің жасаушылары параллель және тең.
- 15. Негізгі формулалар
- 16. Цилиндр: Цилиндрдің түрлеріЦилиндрдің қималары
- 17. Тік цилиндрЕгер жасаушылары цилиндрдің табандарына перпендикуляр, яғни
- 18. Көлбеу цилиндрЕгер цилиндрдің жасаушылары табанына қандай да
- 19. Цилиндрдің қималарыЦилиндр осіне параллель қима Қима тік
- 20. Осьтік қимаБұл цилиндрдің осі арқылы өтетін қима.
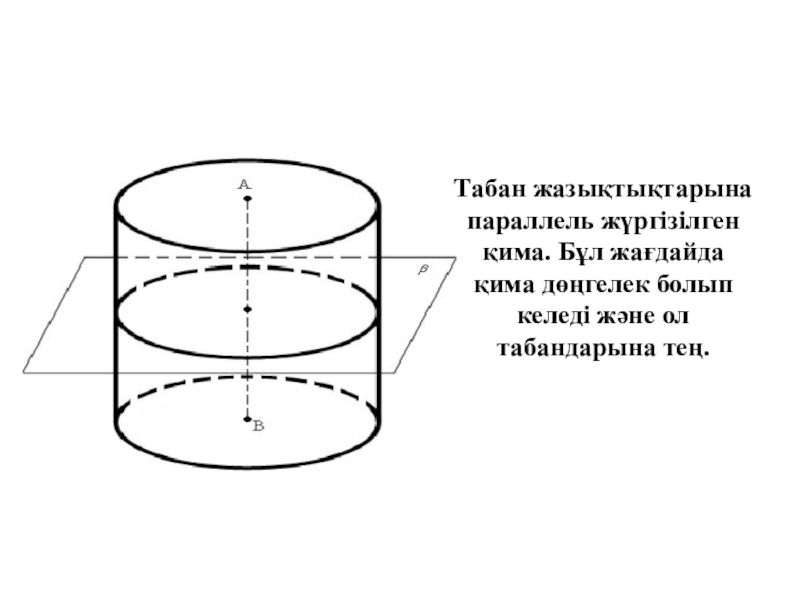
- 21. Табан жазықтықтарына параллель жүргізілген қима. Бұл жағдайда қима дөңгелек болып келеді және ол табандарына тең.Цилиндрдің қималары
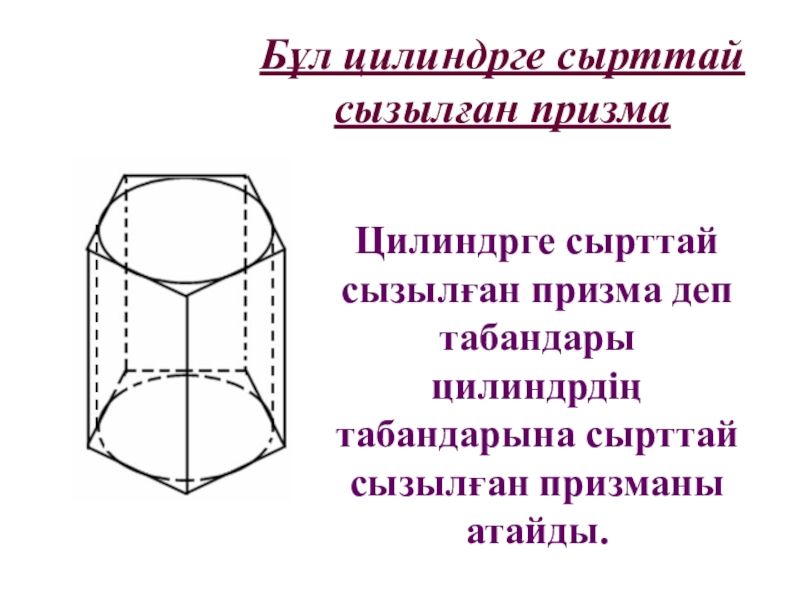
- 22. Бұл цилиндрге сырттай сызылған призмаЦилиндрге сырттай сызылған призма деп табандары цилиндрдің табандарына сырттай сызылған призманы атайды.
- 23. Бұл цилиндрге іштей сызылған призма Цилиндрге іштей
- 24. Цилиндр туралы тусінік.
- 25. Цилиндр - айналу денесі. Анықтама. Цилиндр деп
- 26. Мысалға қандай да бір F фигуррасын L осіне айналдырсақ бізде айналу денесі цилиндр пайда болады. FLF
- 27. (2-сурет) АОО1В тікбұрышын ОО1 қабырғасынан айналдырғанда шыққан
- 28. Цилиндр қимасы Цилиндрдің жазықтықпен қимасы деп жалғыз
- 29. Цилиндр жазбасы мен бетінің ауданы. Цилиндрдің
- 30. Цилиндрдің көлемі.α Тік дөңгелек цилиндрдің әрбір көлденең
- 31. Көлемінің формуласы.Бізге табанының ауданы S және h
- 32. Vцил.=S x h Теорема. Дөңгелек
- 33. Скачать презентанцию
Қайталау.Қандай фигураны шеңбер деп атаймыз?
Слайды и текст этой презентации
Слайд 1Тақырыбы: ШАР
Мақсаты: шеңбердің ұзындығы мен дөңгелектің ауданын қайталау. Шар –геометриялық
фигурасымен таныстыру
Слайд 8Шар — сферамен шектелген дене.Сфера- берілген нүктедең берілген қашықтағы кеңістік
нүктелерінің геометриялық орны.
Шардың беті –сфера.
Слайд 12Цилиндр деп тік төртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын денені
атайды.
Цилиндр
Слайд 13Цилиндрдің элементтері
Дөңгелектер цилиндрдің табандары деп аталады, ал олардың радиусы
цилиндрдің радиусы деп аталады. Дөңгелектердің сәйкес нүктелерін қосатын кесінділерді цилиндрдің
жасаушылары деп атайды.Цилиндрдің биіктігі деп табан жазықтықтарының ара қашықтығын атайды.
Цилиндрдің осі деп табандарының центрлерінен өтетін түзуді атайды.
Слайд 14 Цилиндрдің табандары тең.
Цилиндрдің табандары параллель жазықтықтарда жатады.
Цилиндрдің элементтерінің
қасиеттері
Цилиндрдің жасаушылары параллель және тең.
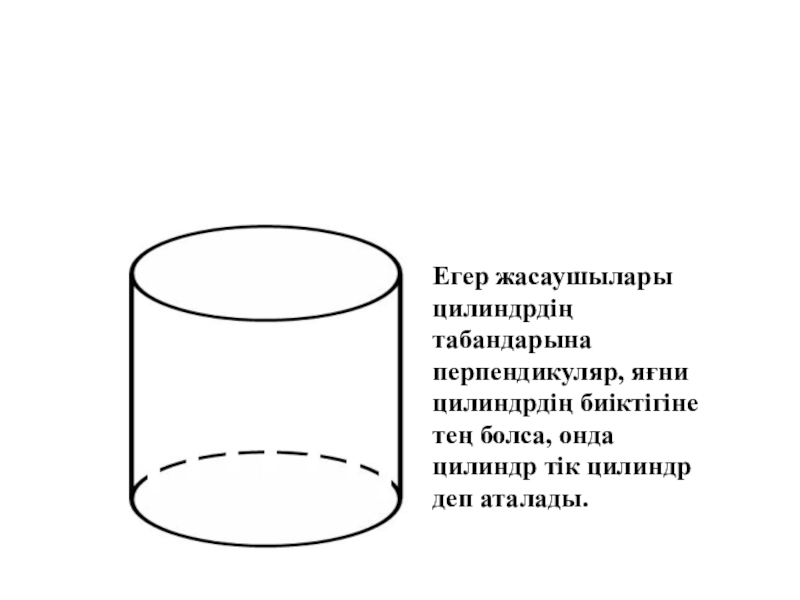
Слайд 17Тік цилиндр
Егер жасаушылары цилиндрдің табандарына перпендикуляр, яғни цилиндрдің биіктігіне тең
болса, онда цилиндр тік цилиндр деп аталады.
Цилиндрдің түрлері
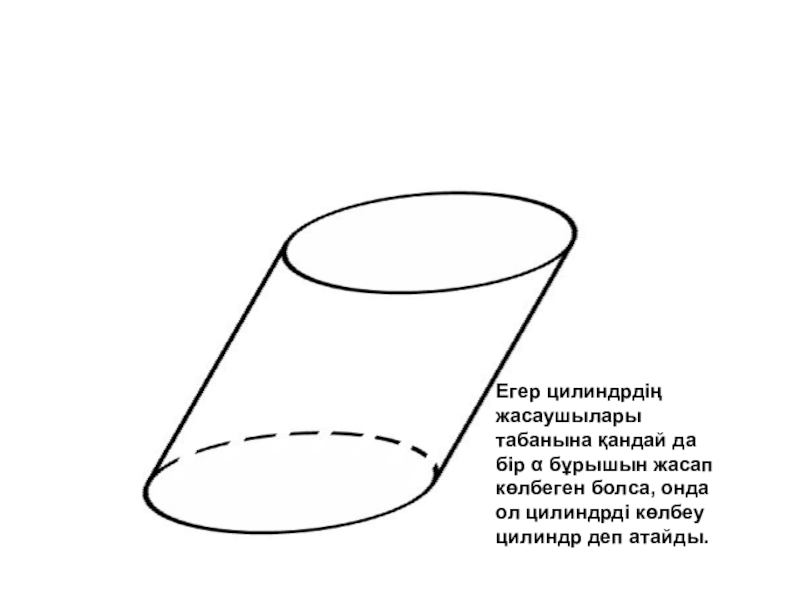
Слайд 18Көлбеу цилиндр
Егер цилиндрдің жасаушылары табанына қандай да бір α бұрышын
жасап көлбеген болса, онда ол цилиндрді көлбеу цилиндр деп атайды.
Цилиндрдің түрлері
Слайд 19Цилиндрдің қималары
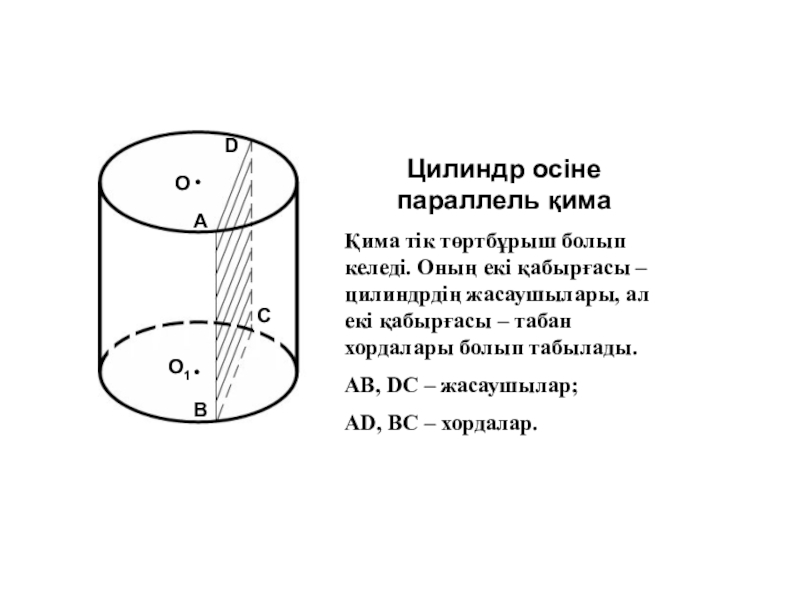
Цилиндр осіне параллель қима
Қима тік төртбұрыш болып келеді.
Оның екі қабырғасы – цилиндрдің жасаушылары, ал екі қабырғасы –
табан хордалары болып табылады.AB, DC – жасаушылар;
AD, BC – хордалар.
А
В
С
D
•
•
О
О1
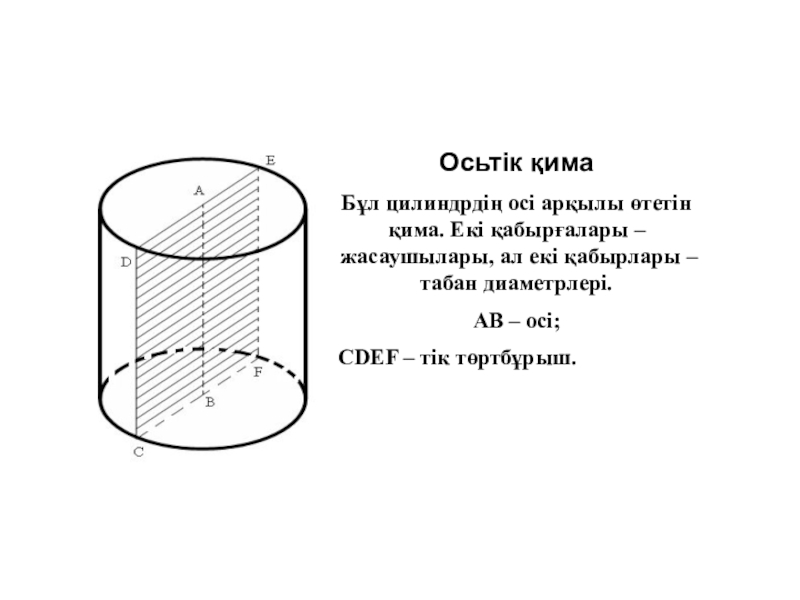
Слайд 20Осьтік қима
Бұл цилиндрдің осі арқылы өтетін қима. Екі қабырғалары –
жасаушылары, ал екі қабырлары – табан диаметрлері.
AB – осі;
CDEF –
тік төртбұрыш.Цилиндрдің қималары
Слайд 21Табан жазықтықтарына параллель жүргізілген қима. Бұл жағдайда қима дөңгелек болып
келеді және ол табандарына тең.
Цилиндрдің қималары
Слайд 22Бұл цилиндрге сырттай сызылған призма
Цилиндрге сырттай сызылған призма деп табандары
цилиндрдің табандарына сырттай сызылған призманы атайды.
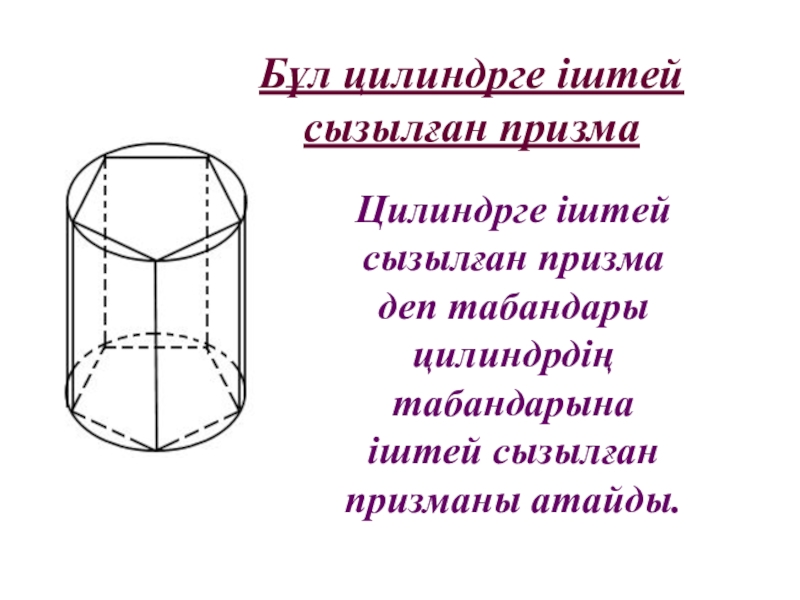
Слайд 23Бұл цилиндрге іштей
сызылған призма
Цилиндрге іштей сызылған призма деп
табандары цилиндрдің табандарына іштей сызылған призманы атайды.
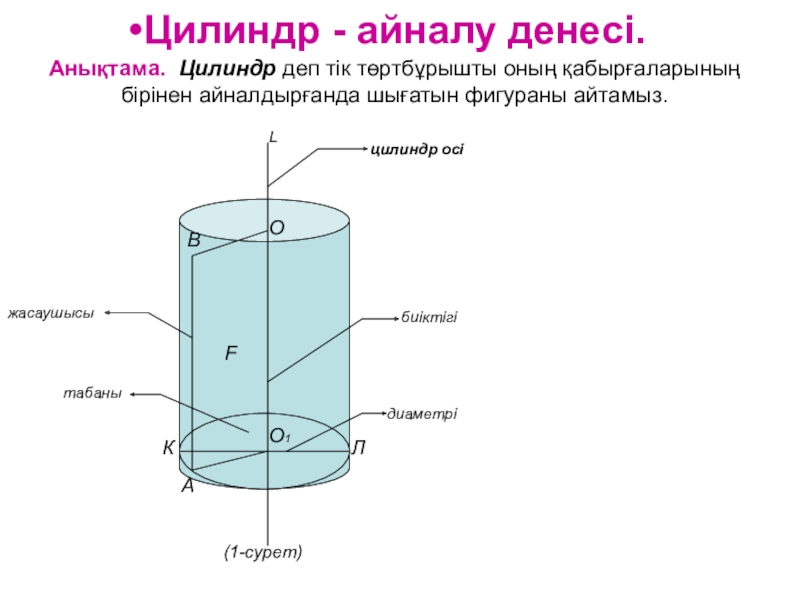
Слайд 25Цилиндр - айналу денесі. Анықтама. Цилиндр деп тік төртбұрышты оның қабырғаларының
бірінен айналдырғанда шығатын фигураны айтамыз.
цилиндр осі
В
А
О
О1
L
F
биіктігі
жасаушысы
К
Л
диаметрі
табаны
(1-сурет)
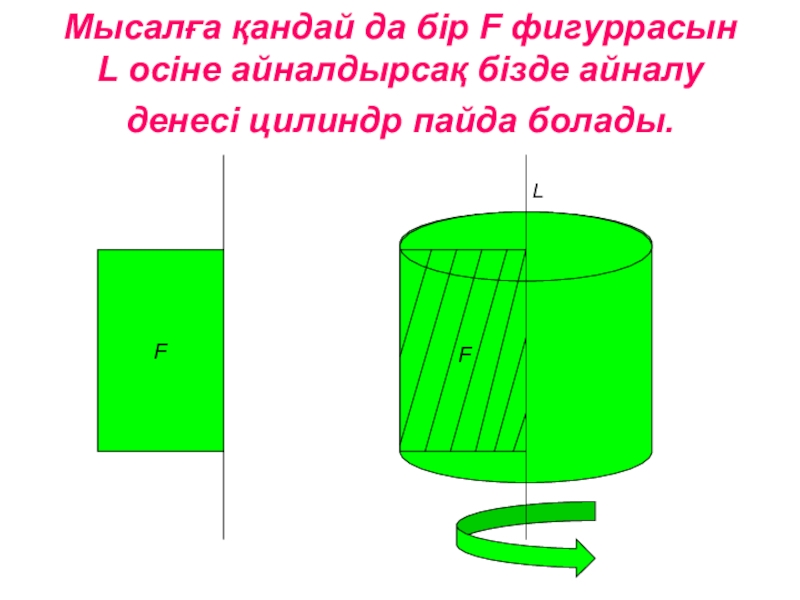
Слайд 26Мысалға қандай да бір F фигуррасын L осіне айналдырсақ бізде
айналу денесі цилиндр пайда болады.
F
L
F
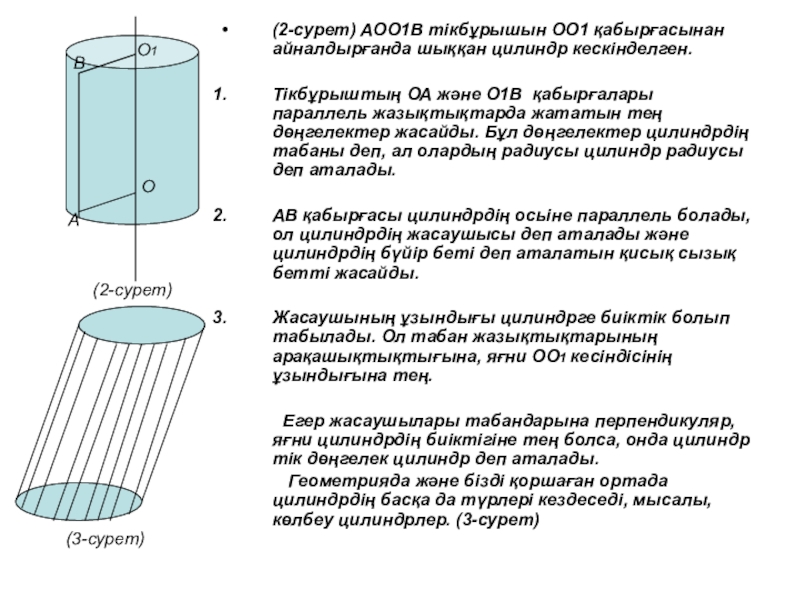
Слайд 27(2-сурет) АОО1В тікбұрышын ОО1 қабырғасынан айналдырғанда шыққан цилиндр кескінделген.
Тікбұрыштың ОА
және О1В қабырғалары параллель жазықтықтарда жататын тең дөңгелектер жасайды. Бұл
дөңгелектер цилиндрдің табаны деп, ал олардың радиусы цилиндр радиусы деп аталады.АВ қабырғасы цилиндрдің осьіне параллель болады, ол цилиндрдің жасаушысы деп аталады және цилиндрдің бүйір беті деп аталатын қисық сызық бетті жасайды.
Жасаушының ұзындығы цилиндрге биіктік болып табылады. Ол табан жазықтықтарының арақашықтықтығына, яғни ОО1 кесіндісінің ұзындығына тең.
Егер жасаушылары табандарына перпендикуляр, яғни цилиндрдің биіктігіне тең болса, онда цилиндр тік дөңгелек цилиндр деп аталады.
Геометрияда және бізді қоршаған ортада цилиндрдің басқа да түрлері кездеседі, мысалы, көлбеу цилиндрлер. (3-сурет)
О1
О
А
В
(2-сурет)
(3-сурет)
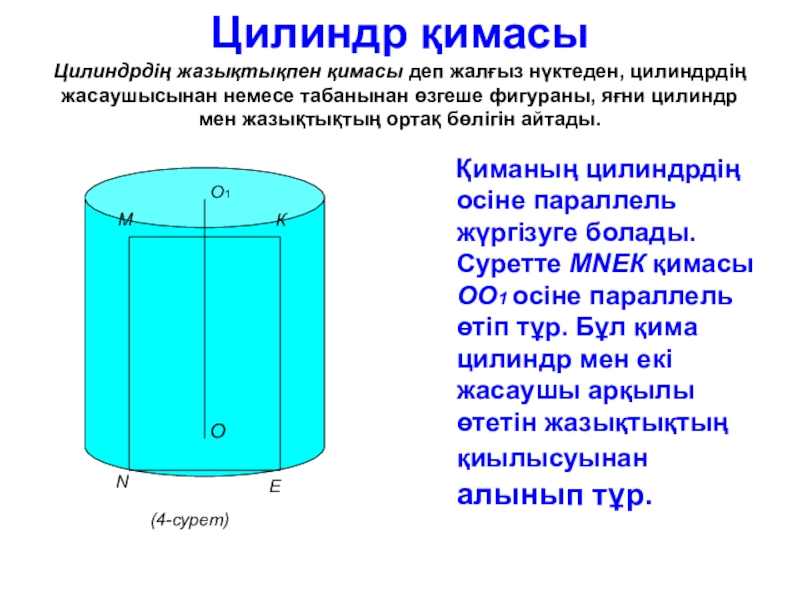
Слайд 28Цилиндр қимасы Цилиндрдің жазықтықпен қимасы деп жалғыз нүктеден, цилиндрдің жасаушысынан немесе
табанынан өзгеше фигураны, яғни цилиндр мен жазықтықтың ортақ бөлігін айтады.
Қиманың цилиндрдің осіне параллель жүргізуге болады. Суретте МNЕК қимасы ОО1 осіне параллель өтіп тұр. Бұл қима цилиндр мен екі жасаушы арқылы өтетін жазықтықтың қиылысуынан алынып тұр.М
К
N
E
О1
О
(4-сурет)
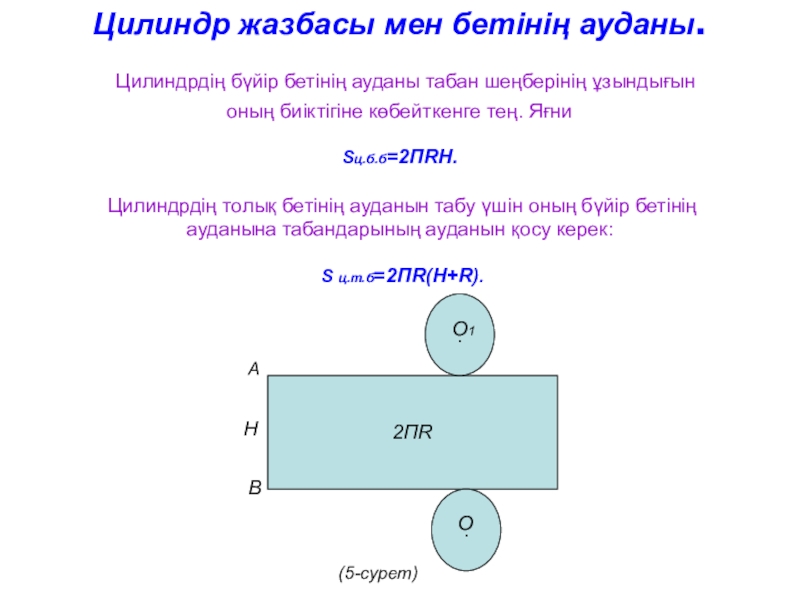
Слайд 29Цилиндр жазбасы мен бетінің ауданы. Цилиндрдің бүйір бетінің ауданы табан
шеңберінің ұзындығын оның биіктігіне көбейткенге тең. Яғни Sц.б.б=2ПRH. Цилиндрдің толық бетінің
ауданын табу үшін оның бүйір бетінің ауданына табандарының ауданын қосу керек: S ц.т.б=2ПR(H+R).2ПR
.
.
А
В
Н
О1
О
(5-сурет)
Слайд 30Цилиндрдің көлемі.
α
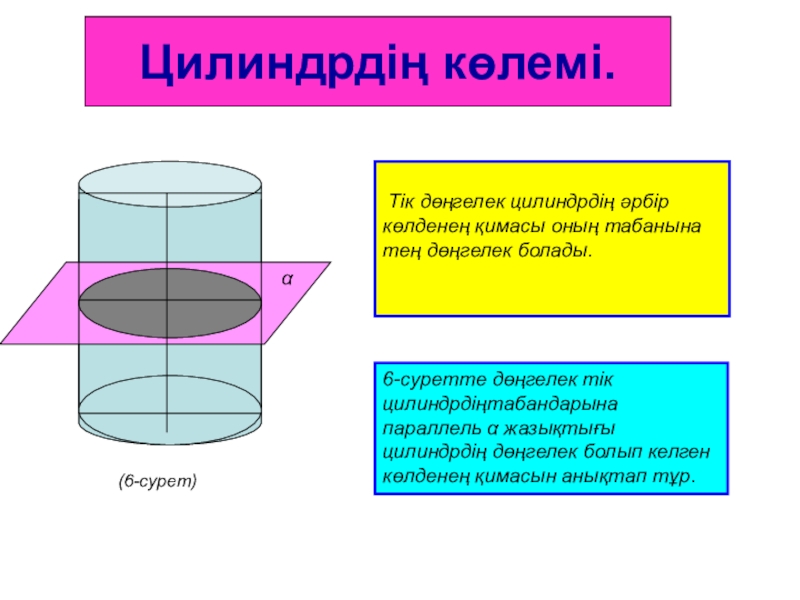
Тік дөңгелек цилиндрдің әрбір көлденең қимасы оның табанына
тең дөңгелек болады.
(6-сурет)
6-суретте дөңгелек тік цилиндрдіңтабандарына параллель α жазықтығы цилиндрдің
дөңгелек болып келген көлденең қимасын анықтап тұр.
Слайд 31Көлемінің формуласы.
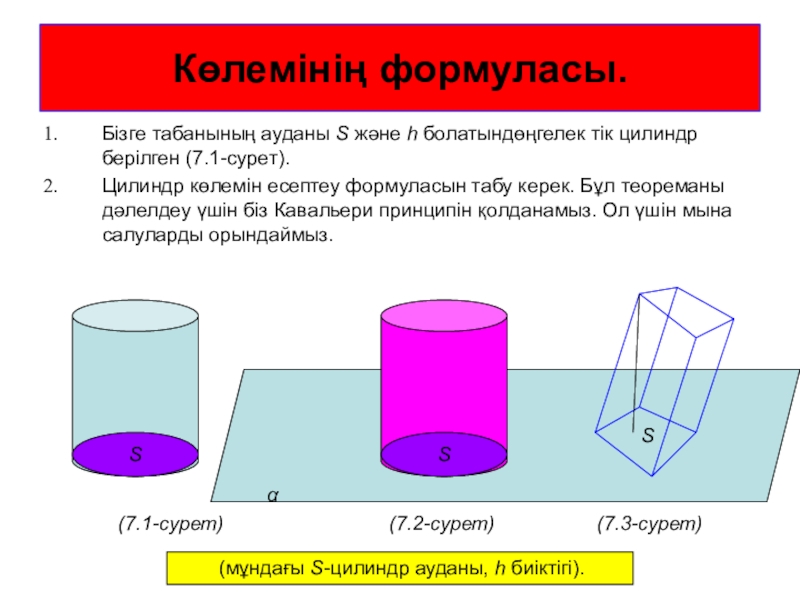
Бізге табанының ауданы S және h болатындөңгелек тік цилиндр
берілген (7.1-сурет).
Цилиндр көлемін есептеу формуласын табу керек. Бұл теореманы
дәлелдеу үшін біз Кавальери принципін қолданамыз. Ол үшін мына салуларды орындаймыз.S
S
S
α
(7.1-сурет)
(7.2-сурет)
(7.3-сурет)
(мұндағы S-цилиндр ауданы, h биіктігі).
Слайд 32Vцил.=S x h
Теорема. Дөңгелек тік цилиндрдің көлемі
оның ауданы мен биіктігінің көбейтіндісіне тең.
Табанының
ауданы берілген цилиндрдің табан ауданына тең призма саламыз. Призма α жазықтығында және оның бір бетіне орналасатындай етіп саламыз. Призманың биіктігі призманың биіктігіне тең болуы тиіс (7.2-сурет).
