Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что нам стоит дом постороить
Содержание
- 1. Что нам стоит дом постороить
- 2. НЕМНОГО ИСТОРИИИСКУССТВО ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР БЫЛО В
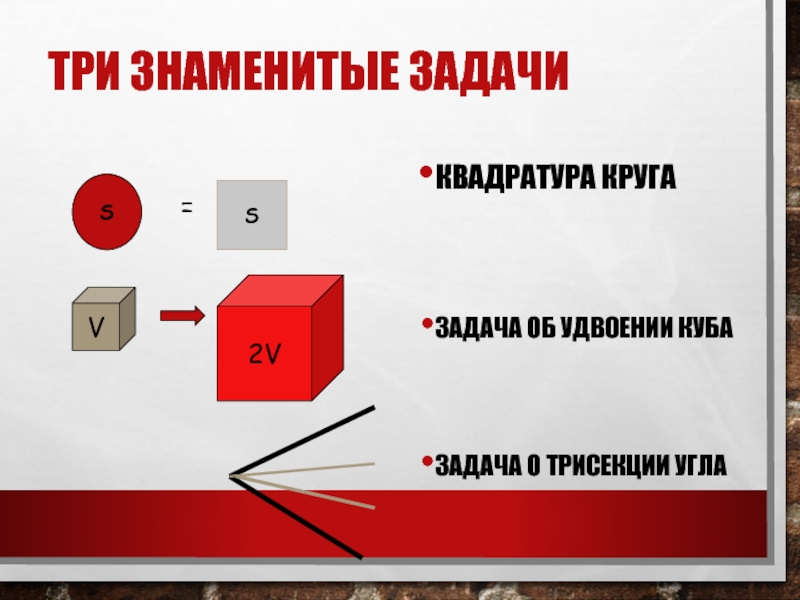
- 3. ТРИ ЗНАМЕНИТЫЕ ЗАДАЧИКВАДРАТУРА КРУГАЗАДАЧА ОБ УДВОЕНИИ КУБАЗАДАЧА О ТРИСЕКЦИИ УГЛА
- 4. ЭВАРИСТА ГАЛУАТОЛЬКО В XΙX ВЕКЕ БЫЛО ДОКАЗАНО,
- 5. ЛИНЕЙКА НЕ ИМЕЕТ ДЕЛЕНИЙ И ИМЕЕТ ТОЛЬКО
- 6. В ЗАДАЧАХ НА ПОСТРОЕНИЕ ВОЗМОЖНЫ СЛЕДУЮЩИЕ ОПЕРАЦИИ,
- 7. С ПОМОЩЬЮ ЛИНЕЙКИ ПРОВЕСТИ ПРЯМУЮ, ПРОХОДЯЩУЮ ЧЕРЕЗ ДВЕ ПОСТРОЕННЫЕ ТОЧКИ.
- 8. С ПОМОЩЬЮ ЦИРКУЛЯ ПРОВЕСТИ ОКРУЖНОСТЬ С ЦЕНТРОМ
- 9. ПОСТРОЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКАПОСТРОИМ ОКРУЖНОСТЬ РАДИУСОМ RОТМЕТИМ НА
- 10. РАЗБИЕНИЕ ОТРЕЗКА НА ДВЕ РАВНЫЕ ЧАСТИ.ЦИРКУЛЕМ И
- 11. ОКРУЖНОСТЬ АПОЛЛОНИЯСТРОИМ ТОЧКИ P И Q, ДЕЛЯЩИЕ
- 12. ПОСТРОЕНИЯ ОДНИМ ЦИРКУЛЕМ.С ПОМОЩЬЮ ОДНОГО ЦИРКУЛЯ МОЖНО
- 13. ПОСТРОЕНИЕ ТОЧКИ, СИММЕТРИЧНОЙ ДАННОЙ ОТНОСИТЕЛЬНО ДАННОЙ ПРЯМОЙ.СТРОИМ ОКРУЖНОСТЬ (А;АС)СТРОИМ ОКРУЖНОСТЬ (В;ВС)ОКР.(А;АС)К - ИСКОМАЯ ТОЧКАокр.(В;ВС)= К
- 14. ПОСТРОЕНИЕ ОДНОЙ ЛИНЕЙКОЙ.В 1833 ГОДУ ШВЕЙЦАРСКИЙ ГЕОМЕТР
- 15. ПОСТРОЕНИЕ БЕЗ ЦИРКУЛЯ.ЗАДАЧА:ИЗ ТОЧКИ А ЛЕЖАЩЕЙ ВНЕ
- 16. ПОСТРОЕНИЕ ДВУСТОРОННЕЙ ЛИНЕЙКОЙ.ЗАДАЧА: ПОСТРОИТЬ БИССЕКТРИСУ ДАННОГО
- 17. ПОСТРОЕНИЕ С ПОМОЩЬЮ ПРЯМОГО УГЛАЗАДАЧА: РАЗДЕЛИТЬ ДАННЫЙ ОТРЕЗОК
- 18. ЗАДАЧИ И НЕ ТОЛЬКО.
- 19. ЗАДАЧИ И НЕ ТОЛЬКО
- 20. всем спасибо!
- 21. Скачать презентанцию
НЕМНОГО ИСТОРИИИСКУССТВО ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР БЫЛО В ВЫСОКОЙ СТЕПЕНИ РАЗВИТО В ДРЕВНЕЙ ГРЕЦИИ. ДРЕВНЕГРЕЧЕСКИЕ МАТЕМАТИКИ ЕЩЕ 3000 ЛЕТ НАЗАД ПРОВОДИЛИ СВОИ ПОСТРОЕНИЯ С ПОМОЩЬЮ ДВУХ ПРИБОРОВ: ГЛАДКОЙ ДОЩЕЧКИ С РОВНЫМ КРАЕМ
Слайды и текст этой презентации
Слайд 4ЭВАРИСТА ГАЛУА
ТОЛЬКО В XΙX ВЕКЕ БЫЛО ДОКАЗАНО, ЧТО ВСЕ ТРИ
ЗАДАЧИ НЕ ИМЕЮТ РЕШЕНИЯ. ВОПРОС НЕВОЗМОЖНОСТИ ПОСТРОЕНИЯ ПОЛНОСТЬЮ РЕШЕН АЛГЕБРАИЧЕСКИМИ
МЕТОДАМИ, ОСНОВАННЫМИ НА ТЕОРИИ ГАЛУА.
Слайд 5ЛИНЕЙКА НЕ ИМЕЕТ ДЕЛЕНИЙ И ИМЕЕТ ТОЛЬКО ОДНУ СТОРОНУ БЕСКОНЕЧНОЙ
ДЛИНЫ.
ЦИРКУЛЬ ИМЕЕТ СКОЛЬ УГОДНО БОЛЬШОЙ РАЗМЕР
Слайд 6В ЗАДАЧАХ НА ПОСТРОЕНИЕ ВОЗМОЖНЫ СЛЕДУЮЩИЕ ОПЕРАЦИИ, ИЗВЕСТНЫЕ С ДРЕВНИХ
ВРЕМЕН:
ВЫБОР ПРОИЗВОЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ
НАХОЖДЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ПОСТРОЕННЫХ
ЛИНИЙ.ВЫБОР ТОЧКИ НА ПРЯМОЙ
Слайд 8С ПОМОЩЬЮ ЦИРКУЛЯ ПРОВЕСТИ ОКРУЖНОСТЬ С ЦЕНТРОМ В ПОСТРОЕННОЙ ТОЧКЕ
И С РАДИУСОМ, РАВНЫМ РАССТОЯНИЮ МЕЖДУ ДВУХ ПОСТРОЕННЫХ ТОЧЕК.
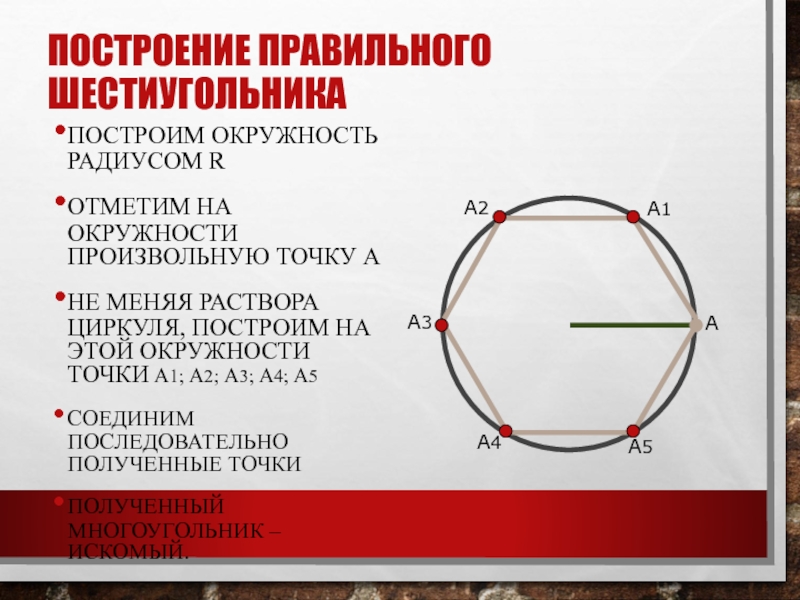
Слайд 9ПОСТРОЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА
ПОСТРОИМ ОКРУЖНОСТЬ РАДИУСОМ R
ОТМЕТИМ НА ОКРУЖНОСТИ ПРОИЗВОЛЬНУЮ ТОЧКУ
А
НЕ МЕНЯЯ РАСТВОРА ЦИРКУЛЯ, ПОСТРОИМ НА ЭТОЙ ОКРУЖНОСТИ ТОЧКИ А1;
А2; А3; А4; А5СОЕДИНИМ ПОСЛЕДОВАТЕЛЬНО ПОЛУЧЕННЫЕ ТОЧКИ
ПОЛУЧЕННЫЙ МНОГОУГОЛЬНИК – ИСКОМЫЙ.
А
А1
А2
А3
А4
А5
Слайд 10РАЗБИЕНИЕ ОТРЕЗКА НА ДВЕ РАВНЫЕ ЧАСТИ.
ЦИРКУЛЕМ И ЛИНЕЙКОЙ ПРОВОДИМ ОКРУЖНОСТЬ
С ЦЕНТРОМ В ТОЧКЕ А И РАДИУСОМ АВ
ПРОВОДИМ ОКРУЖНОСТЬ С
ЦЕНТРОМ В ТОЧКЕ В РАДИУСОМ АВНАХОДИМ ТОЧКИ ПЕРЕСЕЧЕНИЯ P И Q ДВУХ ПОСТРОЕННЫХ ОКРУЖНОСТЕЙ
ЛИНЕЙКОЙ ПРОВОДИМ ОТРЕЗОК, СОЕДИНЯЮЩИЙ ТОЧКИ P И Q
НАХОДИМ ТОЧКУ ПЕРЕСЕЧЕНИЯ АВ И PQ ТОЧКУ К. К – ИСКОМАЯ СЕРЕДИНА ОТРЕЗКА АВ
P
Q
A
B
К
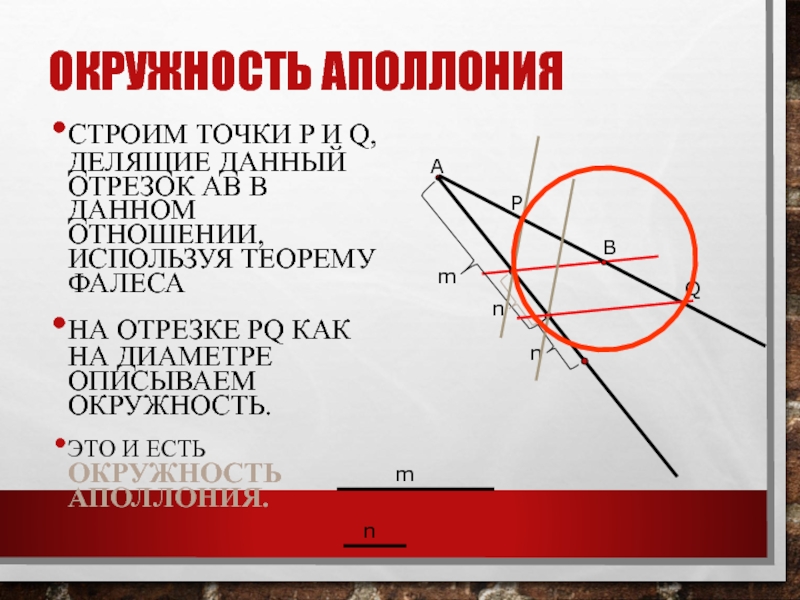
Слайд 11ОКРУЖНОСТЬ АПОЛЛОНИЯ
СТРОИМ ТОЧКИ P И Q, ДЕЛЯЩИЕ ДАННЫЙ ОТРЕЗОК АВ
В ДАННОМ ОТНОШЕНИИ, ИСПОЛЬЗУЯ ТЕОРЕМУ ФАЛЕСА
НА ОТРЕЗКЕ PQ КАК НА
ДИАМЕТРЕ ОПИСЫВАЕМ ОКРУЖНОСТЬ. ЭТО И ЕСТЬ ОКРУЖНОСТЬ АПОЛЛОНИЯ.
A
B
m
n
n
P
Q
m
n
Слайд 12ПОСТРОЕНИЯ ОДНИМ ЦИРКУЛЕМ.
С ПОМОЩЬЮ ОДНОГО ЦИРКУЛЯ МОЖНО ПОСТРОИТЬ ЛЮБУЮ ФИГУРУ,
КОТОРУЮ МОЖНО ПОСТРОИТЬ ЦИРКУЛЕМ И ЛИНЕЙКОЙ. ПРИ ЭТОМ ПРЯМАЯ СЧИТАЕТСЯ
ПОСТРОЕННОЙ, ЕСЛИ НА НЕЙ ЗАДАНЫ ДВЕ ТОЧКИ.ПО ТЕОРЕМЕ МОРА – МАКЕРОНИ.
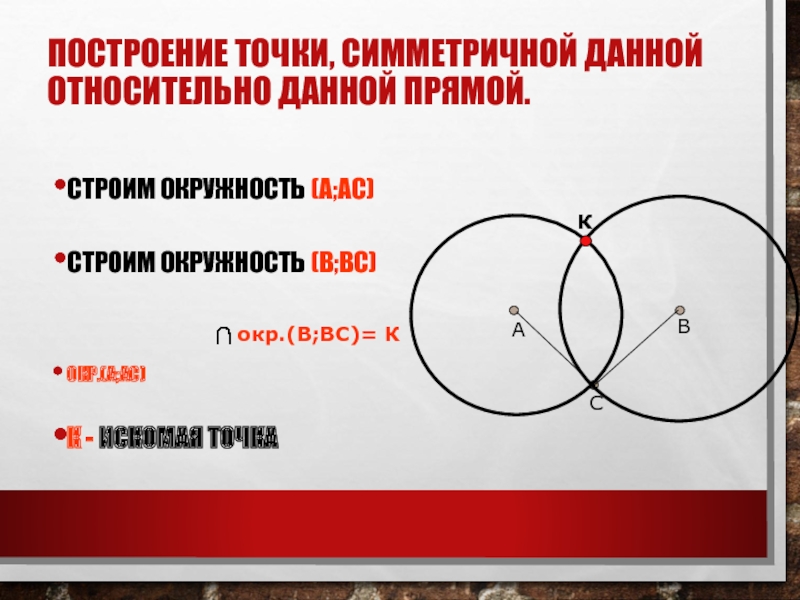
Слайд 13ПОСТРОЕНИЕ ТОЧКИ, СИММЕТРИЧНОЙ ДАННОЙ ОТНОСИТЕЛЬНО ДАННОЙ ПРЯМОЙ.
СТРОИМ ОКРУЖНОСТЬ (А;АС)
СТРОИМ ОКРУЖНОСТЬ
(В;ВС)
ОКР.(А;АС)
К - ИСКОМАЯ ТОЧКА
окр.(В;ВС)= К
Слайд 14ПОСТРОЕНИЕ ОДНОЙ ЛИНЕЙКОЙ.
В 1833 ГОДУ ШВЕЙЦАРСКИЙ ГЕОМЕТР ЯКОБ ШТЕЙНЕР ОПУБЛИКОВАЛ
РАБОТУ, В КОТОРОЙ ПОЛНО ИССЛЕДОВАЛ ПОСТРОЕНИЯ ОДНОЙ ЛИНЕЙКОЙ. В РАБОТЕ
ОН ДОКАЗАЛ ТЕОРЕМУ:«КАЖДАЯ ЗАДАЧА НА ПОСТРОЕНИЕ, РАЗРЕШИМАЯ ЦИРКУЛЕМ И ЛИНЕЙКОЙ, МОЖЕТ БЫТЬ РЕШЕНА И ОДНОЙ ЛИНЕЙКОЙ, ЕСЛИ В ПЛОСКОСТИ ЧЕРТЕЖА ДАНА ПОСТОЯННАЯ ОКРУЖНОСТЬ И ЕЕ ЦЕНТР».
ЭТО ТЕОРЕМА ПОНСЕЛЕ –ШТЕЙНЕРА. (В 1822 ГОДУ ЭТА ТЕОРЕМА БЫЛА ДОКАЗАНА ДРУГИМ СПОСОБОМ ФРАНЦУЗОМ Ж. ПОНСЕЛЕ).
Слайд 15ПОСТРОЕНИЕ БЕЗ ЦИРКУЛЯ.
ЗАДАЧА:
ИЗ ТОЧКИ А ЛЕЖАЩЕЙ ВНЕ ДАННОЙ ОКРУЖНОСТИ, ОПУСТИТЬ
НА ЕЕ ДИАМЕТР ПЕРПЕНДИКУЛЯР, ОБХОДЯСЬ ПРИ ЭТОМ БЕЗ ЦИРКУЛЯ. ЦЕНТР
ОКРУЖНОСТИ НЕ УКАЗАН.РЕШЕНИЕ:
СОЕДИНИМ А С В И С, ПОЛУЧИМ ТОЧКИ D И E
ВЫСОТЫ ВЕ И СD ПЕРЕСЕКАЮТСЯ В ТОЧКЕ М
СОЕДИНИМ ТОЧКИ А И М
АМ – ИСКОМЫЙ ПЕРПЕНДИКУЛЯР.
А
В
С
D
E
M
Все высоты треугольника пересекаются в одной точке
Слайд 16ПОСТРОЕНИЕ ДВУСТОРОННЕЙ ЛИНЕЙКОЙ.
ЗАДАЧА:
ПОСТРОИТЬ БИССЕКТРИСУ ДАННОГО УГЛА АВС
РЕШЕНИЕ:
ПРОВЕСТИ ПРЯМЫЕ
ПАРАЛЛЕЛЬНЫЕ СТОРОНАМ УГЛА
К – ТОЧКА ПЕРЕСЕЧЕНИЯ ЭТИХ ПРЯМЫХ
ПРОВЕСТИ ПРЯМУЮ ЧЕРЕЗ
ВЕРШИНУ УГЛА А И ТОЧКУ КАК – ИСКОМАЯ БИССЕКТРИСА
В
А
С
Слайд 17ПОСТРОЕНИЕ С ПОМОЩЬЮ ПРЯМОГО УГЛА
ЗАДАЧА:
РАЗДЕЛИТЬ ДАННЫЙ ОТРЕЗОК ПОПОЛАМ
РЕШЕНИЕ:
ПОСТРОИМ ПРЯМОУГОЛЬНИК ACBD
, ГДЕ АВ – ДИАГОНАЛЬ.
НАЙДЕМ ТОЧКУ ПЕРЕСЕЧЕНИЯ ДИАГОНАЛЕЙ ПРЯМОУГОЛЬНИКА.
О –
ИСКОМАЯ ТОЧКА прямой угол- две стороны чертежного треугольника
А
В
C
D
О
