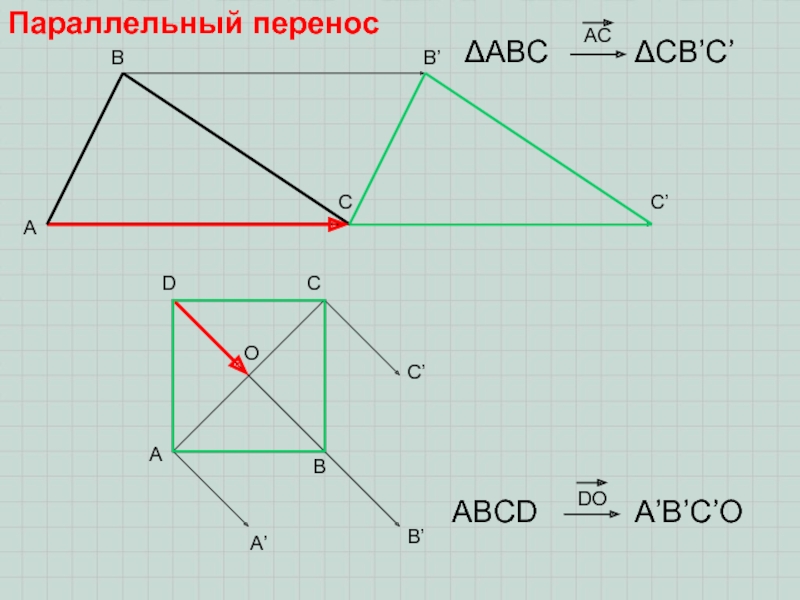
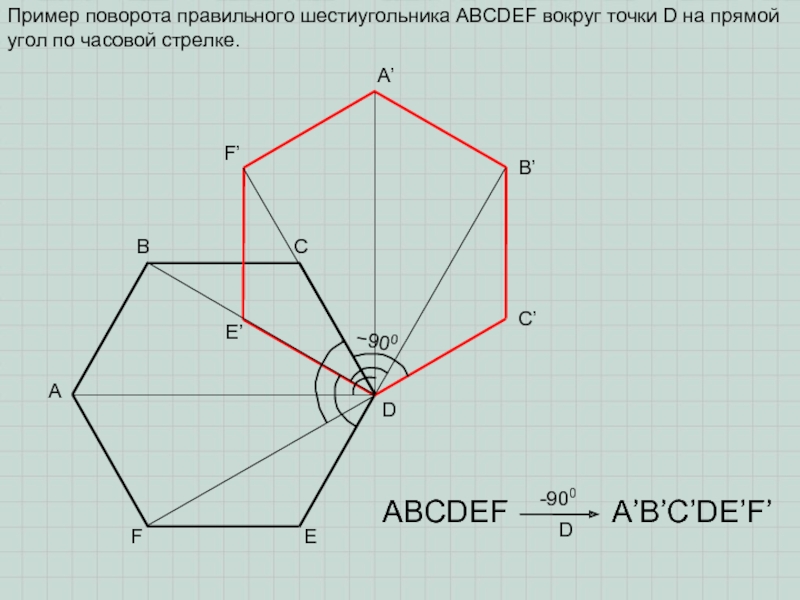
называется движением.
Из определения следует, что при движении любой фигуры на
плоскости, в результате получается, равная данной, фигура.O
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
A
B
C
A’
B’
p
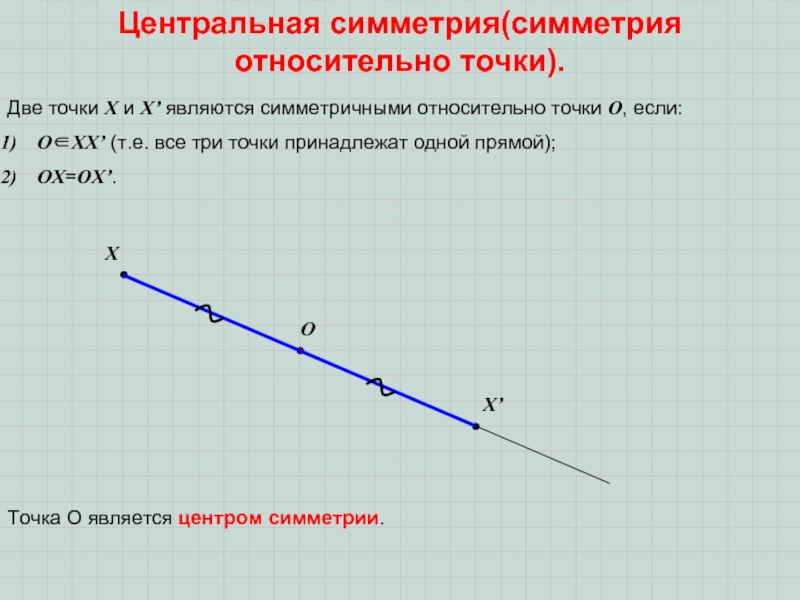
Рассмотрим виды движения подробнее.