Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы математической статиститки
Содержание
- 1. Элементы математической статиститки
- 2. Статистика – дизайн информации
- 3. Цель:Дать понятие генеральной и выборочной совокупности, полигону
- 4. Генеральная совокупность и выборка Опр 1: Генеральной
- 5. Опр 4: Если выборку отбирают по одному
- 6. Статистическое распределение выборки Пусть из генеральной совокупности
- 7. Опр 7: Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
- 8. Опр 8: Полигоном частот называют ломанную отрезки
- 9. Опр 9: Гистограммой частот называют ступенчатую фигуру,
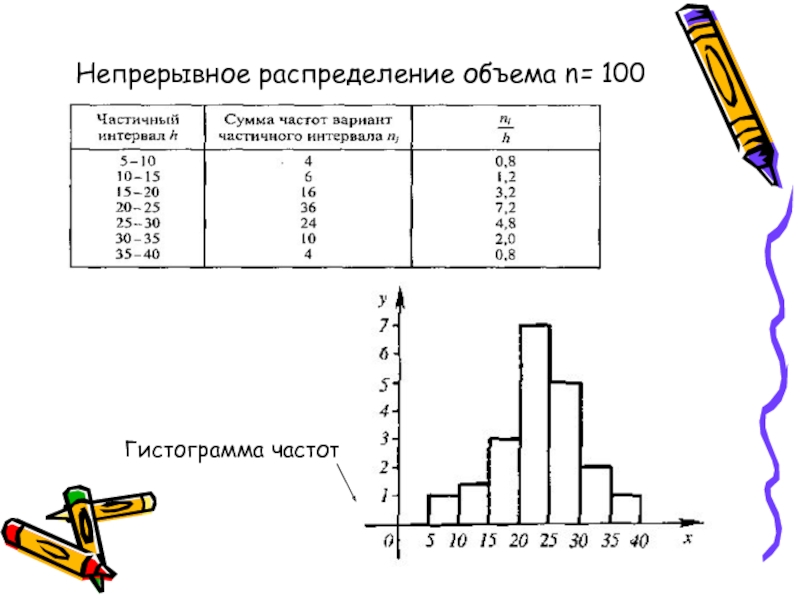
- 10. Непрерывное распределение объема n= 100Гистограмма частот
- 11. Оценка параметров генеральной совокупности Опр 10: Статистической
- 12. Опр 12: Несмещенной называют точечную оценку, математическое
- 13. Опр 14: Выборочной средней называют
- 14. Несмещенной оценкой генеральной средней (математического ожидания)
- 15. Несмещенной оценкой генеральной дисперсии служит исправленная выборочная
- 16. Выборочным средним квадратическим отклонением (стандартом) называют квадратный
- 17. Доверительный интервал – это интервал, который с заданной вероятностью покрывает неизвестную характеристику.
- 18. Доверительный интервал
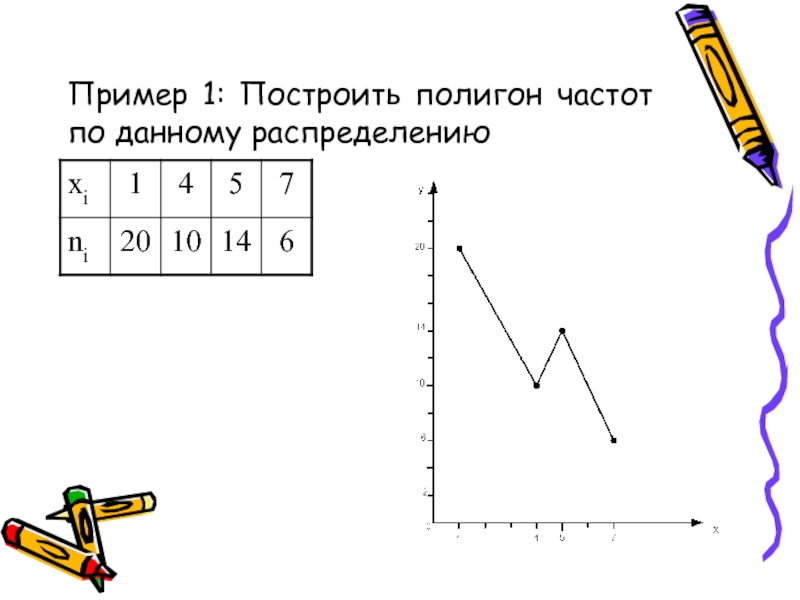
- 19. Пример 1: Построить полигон частот по данному распределению
- 20. Пример 2: Наблюдая за работой
- 21. Решение:
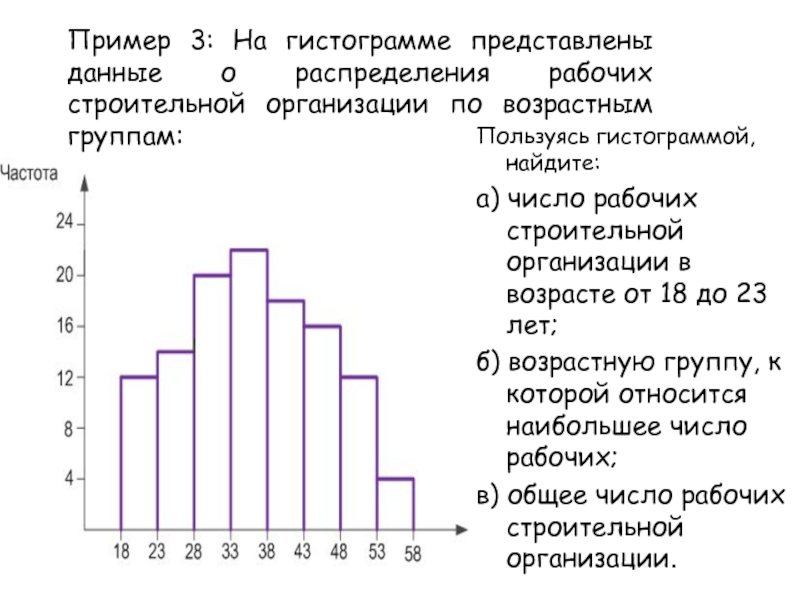
- 22. Пример 3: На гистограмме представлены данные о
- 23. Независимо от того, в какой отрасли знания
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Цель:
Дать понятие генеральной и выборочной совокупности, полигону и гистограмме частот
Научиться
строить полигон и гистограмму частот
Слайд 4Генеральная совокупность и выборка
Опр 1: Генеральной совокупностью называется совокупность,
из которой отбирают часть объектов.
Опр 2: Выборка (или выборочная совокупность)
- это множество объектов, случайно отобранных из генеральной совокупности.Опр 3: Число объектов генеральной совокупности и выборки называют соответственно объемом генеральной совокупности и объемом выборки.
Слайд 5Опр 4: Если выборку отбирают по одному объекту, который обследуют
и снова возвращают в генеральную совокупность, то выборка называется повторной.
Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной.Слайд 6Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем
x1, x2, … xk объёма N.
Опр 5: Наблюдаемые значения x1,
x2, … xk называют вариантами, а последовательность вариант, записанная в возрастающем порядке, - вариационным рядом. Опр 6: Числа наблюдений n1, n2, …nk называют частотами, а их отношения к объему
, , …,
- относительными частотами.
Сумма относительных частот равна единице:
Слайд 7Опр 7: Статистическим распределением выборки называют перечень вариант и соответствующих
им частот или относительных частот.
Слайд 8Опр 8: Полигоном частот называют ломанную отрезки которой соединяют точки
.
Для построения полигона на оси Ох откладывают значения вариант xi,
на оси Оу - значения частот ni (относительных частот ωi).Полигон частот
Слайд 9Опр 9: Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников,
основаниями которых служат частичные интервалы длины h, а высоты равны
отношению (плотность частоты).
Слайд 11Оценка параметров генеральной совокупности
Опр 10: Статистической оценкой Θ* неизвестного
параметра Θ теоретического распределения называют функцию
от наблюдаемых случайных величин .Опр 11: Точечной называют статистическую оценку, которая определяется одним числом
, где -
результаты n наблюдений над количественным признаком X (выборка).
Слайд 12Опр 12: Несмещенной называют точечную оценку, математическое ожидание которой равно
оцениваемому параметру при любом объеме выборки.
Опр 13: Смещенной называют точечную
оценку, математическое ожидание которой не равно оцениваемому параметру.Слайд 13Опр 14: Выборочной средней называют среднее арифметическое значений
признака выборочной совокупности.
Опр 15: Выборочной дисперсией Dв называется среднее арифметическое
квадратов отклонений наблюдаемых значений признака X от выборочного среднего .
Слайд 14Несмещенной оценкой генеральной средней (математического ожидания)
служит выборочная
средняя
,где xi – варианта выборки, ni – частота варианты xi ,
- объем выборки.
Слайд 15Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
Смещенной оценкой генеральной дисперсии служит выборочная
дисперсия
Слайд 16Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной
дисперсии .
Слайд 17Доверительный интервал – это интервал, который с заданной вероятностью покрывает
неизвестную характеристику.
Слайд 18 Доверительный интервал для математического ожидания
где - аргумент распределения Стьюдента, соответствующей доверительной вероятности γ и (N-1) степени свободы.
Слайд 20 Пример 2: Наблюдая за работой бригады токарей, установили, сколько времени
тратили они на обработку одной детали. Обобщая полученные данные составили
таблицу.Пользуясь таблицей, постройте гистограмму частот, характеризующую распределение токарей бригады по времени, затрачиваемому на обработку одной детали.
Слайд 22Пример 3: На гистограмме представлены данные о распределения рабочих строительной
организации по возрастным группам:
Пользуясь гистограммой, найдите:
а) число рабочих строительной организации
в возрасте от 18 до 23 лет;б) возрастную группу, к которой относится наибольшее число рабочих;
в) общее число рабочих строительной организации.
Слайд 23Независимо от того, в какой отрасли знания получены числовые данные,
они обладают определёнными свойствами, для выявления которых может потребоваться особого
рода научный метод обработки. Последний известен как статистический метод или, короче, статистика.Дж.Юл.М.Кендалл,
«Теория статистики»