Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формирование жизненных компетентностей на уроках математики.
Содержание
- 1. Формирование жизненных компетентностей на уроках математики.
- 2. Мастер-класс учителя математики МОУ”Школа №80 города
- 3. «Через математические знания, полученные в школе,
- 4. В условиях реализации требований ГОС наиболее актуальными
- 5. Технология критического мышления Критическое мышление– это способность
- 6. Есть такой закон — закон Меткалфа, формулирующий
- 7. Некоторым программам требуется n² времени для
- 8. Физика. Если вспомнить школьные уроки физики, можно привести
- 9. Можно формировать критическое мышление,решая одну и ту же задачу несколькими способами.
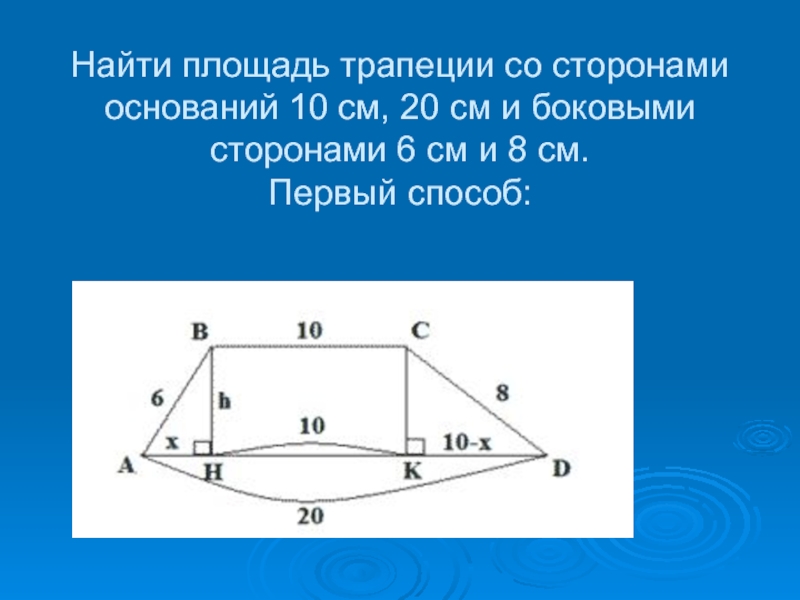
- 10. Найти площадь трапеции со сторонами оснований 10
- 11. Проведем ВНАD и СКАD, тогда четырехугольник ВНКС
- 12. Второй способ:1. Проведем СНАD и СКАВ, тогда
- 13. Третий способ:1. Продолжим АВ до пересечения с
- 14. Четвертый способ:1. Проведем СК||АВ и соединим точки
- 15. Многие педагоги задают вопрос: "Почему не все
- 16. В условиях современного общества предъявляются
- 17. 1. Произведение двух последовательных натуральных чисел равно
- 18. Для начала урока о многогранниках можно рассказать
- 19. Можно предложить нестандартный взгляд на теорему о
- 20. Закончу словами: «В каждой работе есть место
- 21. СПАСИБО ЗА ВНИМАНИЕ!ТВОРЧЕСКИХ УСПЕХОВ!
- 22. Скачать презентанцию
Мастер-класс учителя математики МОУ”Школа №80 города Донецка” Архипцевой Валентины АлександровныТемаФормирование жизненных компетентностей с помощьюновых технологий в свете ГОС
Слайды и текст этой презентации
Слайд 2Мастер-класс
учителя математики
МОУ”Школа №80 города Донецка”
Архипцевой Валентины Александровны
Тема
Формирование жизненных компетентностей
с помощью
Слайд 3 «Через математические знания, полученные в школе, лежит широкая дорога к
огромным, почти необозримым областям
труда и открытий» А. И. МаркушевичСлайд 4В условиях реализации требований ГОС наиболее актуальными становятся технологии: v Информационно –
коммуникационная технология v Технология развития критического мышления v Проектная технология v Технология развивающего
обучения v Здоровьесберегающие технологии v Технология проблемного обучения v Игровые технологии v Модульная технология v Технология мастерских v Кейс – технология v Технология интегрированной уровневой дифференциации v Групповые технологии. v Традиционные технологии Поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, то использование их в изучении материала с использованием ИКТ повышают эффективность обучения.Слайд 5 Технология критического мышления
Критическое мышление– это способность анализировать информацию с
помощью логики и личностно-психологического подхода, с тем, чтобы применять полученные
результаты как к стандартным, так и нестандартным ситуациям, вопросам и проблемам. Этому процессу присуща открытость новым идеям.Например, при изучении теоремы Пифагора можно задать вопрос:
- На что пойдет больше краски: на круг радиуса 5м или на 2 круга радиусами 4м и3м.
- А затем можно расширить представление о применении свойств египетского треугольника на таких примерах.
Слайд 6Есть такой закон — закон Меткалфа, формулирующий уровень полезности социальной
сети: он говорит, что ценность социальной сети растёт в квадратичной
зависимости от количества пользователей в ней. Например: Сеть из 50 млн. пользователей = Сеть из 40 млн. пользователей + Сеть из 30 млн. пользователей Кажется удивительным, что полезность социальной сети в 50 миллионов человек выражается через полезность двух социальных-сетей, в сумме имеющих 70 миллионов человек, но это на самом деле так. Социальная сеть растёт нелинейно..Слайд 7 Некоторым программам требуется n² времени для обработки n запросов. Другими
словами: 50 запросов = 40 запросов + 30 запросов Площадь поверхности. Площадь поверхности
сферы определяется как 4πr². Что это значит? Площадь радиусом 50 = Площадь радиусом 40 + Площадь радиусом 30 В жизни нам встречается не так уж и много сфер, но вот портовым работникам это знание весьма полезно (в конце концов, корпус любого судна — это деформированная сфера). Количеством краски, необходимой для 50-тифутовой яхты, можно окрасить две яхты длиной 40 и 30 футов.Слайд 8Физика.
Если вспомнить школьные уроки физики, можно привести в пример формулу
расчёта кинетической энергии объекта массой m при скорости v: 1/2mv².
Применяем теорему Пифагора.Энергия при скорости в 500 км/ч = Энергия при скорости в 400 км/ч + Энергия при скорости в 300 км/ч
Значит, одного и того же количества энергии хватает либо на запуск одного предмета на скорости 500 км/ч, либо на запуск двух других на меньшей скорости.
Слайд 10Найти площадь трапеции со сторонами оснований 10 см, 20 см
и боковыми сторонами 6 см и 8 см.
Первый способ:
Слайд 11Проведем ВНАD и СКАD, тогда четырехугольник ВНКС – прямоугольник. 2. Пусть
АН=см, тогда КD=(10-) см. Используя теорему Пифагора, выразим высоту h из
АВН и СКD: h , h Составляя и решая уравнение, получим, что х = 3,6(см), а высота h=4,8(см) 3. Тогда S=72(см²)Слайд 12Второй способ:
1. Проведем СНАD и СКАВ, тогда АВСК - параллелограмм,
АК=ВС=10 см и АВ=КС=6 см
2. Рассмотрим КСD: КС=6 см, СD=8
см, КD=10 см. Так как КD= КССD, то по теореме, обратной теореме Пифагора, КСD - прямоугольный.3. Можно найти высоту по формуле: СН=(см²)
4. Площадь трапеции находим, так же как и в первом решении
Слайд 13Третий способ:
1. Продолжим АВ до пересечения с СD в точке
Е, проведем СК АВ.
2. Устанавливаем, что КСD– прямоугольный и АВСК-
параллелограмм.3. AЕD и КСD подобны по первому признаку (D- общий, КСD=АЕD по свойству
параллельных прямых), коэффициент подобия k=2, так как k =
4. Отсюда АЕ=KC•k=12 см, DE= DC•k = 16 см.
5. Так как AЕD и КСD- прямоугольные, то S (см)
S(см). Площадь AЕD можно было найти через отношение площадей подобных треугольников:
Теперь можно найти площадь трапеции: S=S(см)
Слайд 14Четвертый способ:
1. Проведем СК||АВ и соединим точки К и В
отрезком.
2. Нетрудно доказать, что ∆АВК, ∆ВКС, ∆КСD равные и прямоугольные.
3.
S=3•S=3•24=72 (см²)Слайд 15
Многие педагоги задают вопрос: "Почему не все дети включаются в
учебный процесс?" Одна из причин этого - индивидуальность каждого ребенка,
которая и определяет индивидуальный путь к познанию. Использование различных современных педагогических технологий позволяет разнообразить учебный процесс и тем самым вовлекать в активный процесс познания большее количество учащихся. Одной из таких технологий является «Метод проектов». Образовательный потенциал проектной деятельности заключается в возможности: повышение мотивации в получении дополнительных знаний и повышения качества обучения.Например, учащиеся активно создают проекты на тему «Математика вокруг нас»: это применение процентов ,расчет площадей поверхности и объемов предметов домашней обстановки, по экономике задачи на семейный бюджет, расчет прибыли предприятий
Проектная технология
Слайд 16 В условиях современного общества предъявляются все более высокие
требования к ученику как к личности, способной самостоятельно решать проблемы
разного уровня. Возникает необходимость формирования у детей активной жизненной позиции, устойчивой мотивации к образованию и самообразованию, критичности мышления.В этом плане традиционная система обучения имеет значительные недостатки по сравнению с проблемным обучением
Интерес в этом плане вызывают задачи с нестандартным содержанием:
1.Аист пролетел 48 км со скоростью 40 км\час. Сколько при этом он делает взмахов крыльями ,если за каждую секунду он делает 2 взмаха ?
2.Волк и заяц участвовали в соревновании. Каждый прыжок зайца был короче, чем у волка, но прыжки заяц делал втрое чаще, чем волк. Кто победил?
Технология проблемного обучения
Слайд 171. Произведение двух последовательных натуральных чисел равно 132. Найдите сумму
этих чисел, и вы узнаете, сколько пар хромосом в хромосомном
наборе человека.Ответ: 23 пары.
2. За день сердце может перекачать 10 000 литров крови. За сколько дней насос такой мощности смог бы заполнить бассейн длиной 20 метров, шириной 10 метров и глубиной 2 метра?
Ответ:40 дней.
3. Масса витамина С, ежедневно необходимая человеку, относится к массе витамина Е, как 4:1. Какова суточная норма в витамине Е, если витамина С мы в день должны употреблять 60 мг.?
Ответ:15 мг
Слайд 18Для начала урока о многогранниках можно рассказать следующую историю. Однажды
к известному математику А.Н.Колмогорову обратились строители, которые должны были перекрыть
русло речки для постройки гидроэлектростанции. Ученые сделали расчеты и установили, что речку нужно перекрыть бетонными тетраэдрами. Более того они просчитали, что таких правильных тетраэдров должно быть7,5тысяч.Строители засомневались в правильности расчетов и заказали 35 тыс пирамид. Кинули в речку 7,5тысяч и этого оказалось достаточно, а оставшиеся пирамиды остались на берегу как памятник тем, кто не верит в математику.Формирование исследовательских компетентностей можно проследить при решении задач по алгебре в 7-9 классах, когда предлагают решить задачи по парам.
Слайд 19Можно предложить нестандартный взгляд на теорему о трех перпендикулярах или
на аксиому о проведении плоскости через 3 точки,не лежащие на
одной прямой.К нестандартным приемам на уроке можно отнести игровые приемы:игра»ДА-НЕТ»(угадывание предмета в мешке),доказательство свойств геометрических фигур при складывании на моделях,расчет площадей фигур с помощью клетчатой бумаги