Фракталы

Содержание

1. Фракталы
2. Бенуа Мандельброт «Фрактальная геометрия природы»«Почему геометрию
3. Цель работы:Изучить детерминированные(определённые) фракталы
4. Задачи работы:Рассмотреть геометрические фракталы и методы их
5. ФракталФрактал – геометрическая фигура, в которой один
6. Классификация фракталовДетерминированные (алгебраические, геометрические)Недерминированные (стохастические)Природные
7. Детерминированные фракталыДетерминированность (Determination) – определенностьОсновное свойство детерминированных фракталов – свойство самоподобия
8. Геометрические фракталы. Н-фрактал
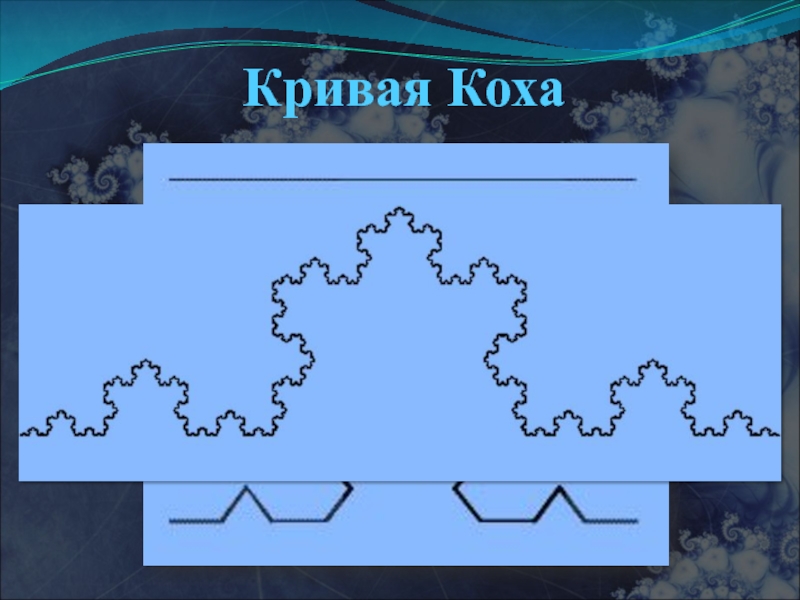
9. Кривая Коха
10. Остров Коха
11. Другие геометрические фракталы
12. Алгебраические фракталы. Множество Мандельброта
13. Алгоритм построенияZ[n+1] = Z[n] * Z[n] + C,где Z и C –комплексные переменные
14. Комплексные числаx – действительное число (R)y –
15. Алгоритм построения Для всех
16. Множество Мандельброта
17. Увеличенная граница множества Мандельброта
18. Множества Мандельброта и Жюлиа
19. Множества Жюлиа С = 0.7+0.3i
20. Множества Жюлиа С = -0.2+0.8i
21. Множества Жюлиа С = -0.5+0.5i
22. Множества Жюлиа С = -0.1+0.7i
23. Построение снежинки в редакторе Adobe PhotoshopОснова:
24. Построение снежинки в редакторе Adobe PhotoshopРезультат:
25. Построение снежинки в редакторе Adobe PhotoshopОснова:
26. Построение снежинки в редакторе Adobe PhotoshopРезультат:
27. Построение снежинки в редакторе Adobe PhotoshopКонечныйрезультат:
28. Построение снежинки в редакторе Adobe PhotoshopОснова:
29. Построение снежинки в редакторе Adobe PhotoshopРезультат:
30. Построение снежинки в редакторе Adobe PhotoshopКонечныйрезультат:
31. Заключение «Если я и видел дальше других,
32. Скачать презентанцию

Бенуа Мандельброт «Фрактальная геометрия природы»«Почему геометрию так часто называют «холодной» и «сухой»? Одна из причин – её неспособность описать форму облака, горы, дерева или береговой линии. Облака не являются конусами,

Слайды и текст этой презентации

Слайд 1Фракталы
МОУ «Гимназия имени Героя Советского Союза Ю.А.Гарнаева»
Руководитель: учитель математики
Афонькина Галина

Ивановна

Слайд 2Бенуа Мандельброт «Фрактальная геометрия природы»
«Почему геометрию так часто называют «холодной»

и «сухой»? Одна из причин – её неспособность описать форму

облака, горы, дерева или береговой линии. Облака не являются конусами, береговые линии нельзя изобразить с помощью окружностей, кору деревьев не назовёшь гладкой, а путь молнии – прямолинейным...»

Бенуа Мандельброт «Фрактальная геометрия природы»«Почему геометрию так часто называют «холодной» и «сухой»? Одна из причин –

Слайд 3Цель работы:
Изучить детерминированные(определённые) фракталы

Слайд 4Задачи работы:
Рассмотреть геометрические фракталы и методы их построения;
Рассмотреть алгебраические фракталы

(Множества Мандельброта и Жюлиа);
Выявить, как меняются алгебраические фракталы при изменении

значения их параметров;

Рассмотреть применение фракталов;

Построить некоторые геометрические фракталы.

Задачи работы:Рассмотреть геометрические фракталы и методы их построения;Рассмотреть алгебраические фракталы (Множества Мандельброта и Жюлиа);Выявить, как меняются алгебраические

Слайд 5Фрактал
Фрактал – геометрическая фигура, в которой один и тот же

фрагмент повторяется при каждом уменьшении масштаба.
Фрактал – самоподобное множество нецелой

дробной размерности.
Фрактал – структура, состоящая из частей, которые в каком-то смысле подобны целому.

ФракталФрактал – геометрическая фигура, в которой один и тот же фрагмент повторяется при каждом уменьшении масштаба.Фрактал –

Слайд 6Классификация фракталов
Детерминированные (алгебраические, геометрические)

Недерминированные (стохастические)

Природные

Слайд 7Детерминированные фракталы
Детерминированность (Determination) – определенность

Основное свойство детерминированных фракталов – свойство

самоподобия

Детерминированные фракталыДетерминированность (Determination) – определенностьОсновное свойство детерминированных фракталов – свойство самоподобия

Слайд 8Геометрические фракталы. Н-фрактал

Слайд 9Кривая Коха

Слайд 10Остров Коха

Слайд 11Другие геометрические фракталы

Слайд 12Алгебраические фракталы. Множество Мандельброта

Слайд 13Алгоритм построения
Z[n+1] = Z[n] * Z[n] + C,

где Z и

C –
комплексные переменные

Слайд 14Комплексные числа
x – действительное число (R)
y – действительное число (R),

коэффициент мнимой части
i – мнимая единица (i*i = -1)
x+yi

Действительная

часть [Re]

Мнимая часть [Im]

Абсолютное значение комплексного числа:

Комплексные числаx – действительное число (R)y – действительное число (R), коэффициент мнимой частиi – мнимая единица (i*i

Слайд 15Алгоритм построения
Для всех точек C на

комплексной плоскости в интервале [-2-i; 1+i] выполняем достаточно большое количество

раз:
Z[n+1] = Z[n] * Z[n] + C,
где Z[0] = 0 (0+0i),
проверяя при этом каждый раз абсолютное значение Z[n+1]. Если оно уходит в бесконечность, рисуем точку белого цвета, если стремится к некоторой постоянной, рисуем точку черного цвета.