Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция
Содержание
- 1. Функция
- 2. Определение функции.Функция – одно из важнейшихматематических понятийФункцией
- 3. ФункцияуПеременную x называют независимой переменной ,
- 4. D(y) и E(y) функцииВсе значениянезависимой переменной х
- 5. Найти D(y) и E(y) функции:y = 3x-5y
- 6. Способы задания функций1. Аналитический2. Графический3.
- 7. График функцииГрафиком функции называют множество всех точек
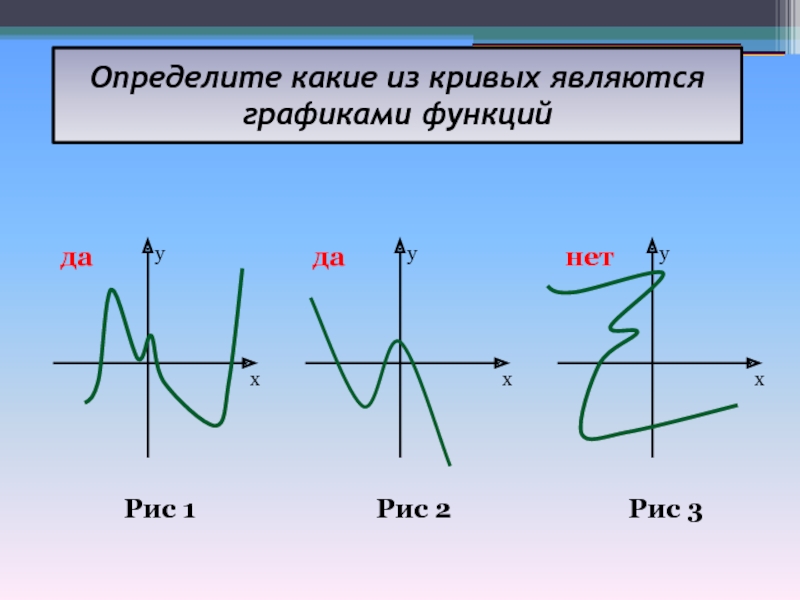
- 8. Определите какие из кривых являются графиками функций Рис 1Рис 2Рис 3yxyxyxдаданет
- 9. Свойства функций1. Чётность:Свойство графикаФункция называется чётной если:
- 10. Свойства функцийНечётностьСвойство графикаФункция называется нечётной если
- 11. Свойства функцийМонотонностьСвойство графикаФункция возрастает[или убывает] на промежутке
- 12. Свойства функцийЗнакопостоянствоСвойство графикаПромежутки, на которых функция сохраняет
- 13. Графи к функцииФункция у:Область определения – D(y)=
- 14. Свойства функций2. ПериодичностьСвойство графикаФункцию f называют периодической
- 15. Область определения-?
- 16. Презентация выполнена учителем
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Определение функции.
Функция –
одно из важнейших
математических понятий
Функцией
называют такую зависимость
переменной у от переменной х,при которой
каждому значению переменной х соответствует единственное значение переменной у
Слайд 3Функция
у
Переменную
x
называют
независимой переменной ,
или
аргументом
Переменную
у
называют
зависимой переменной
Говорят также, что
переменная у является функцией от переменной х
Слайд 4D(y) и E(y) функции
Все значения
независимой переменной
х
образуют
область
определения
функции – D(y)
Все значения ,
которые принимает
зависимая переменная
у
образуют
область значений
функции – E(y)
Слайд 5Найти D(y) и E(y) функции:
y = 3x-5
y = -2x/3
y =
3/2x
y = √1-2x
y = 11sin x
y = lg (4x-1)
x
Є Rx Є R
y Є R
y Є R
x Є (-∞;0)U(0; ∞)
x Є (-∞;0,5]
x Є R
x Є (0,25; ∞)
y Є [0; ∞)
y Є [-11; 11]
y Є R
уЄ (-∞;0)U(0; ∞)
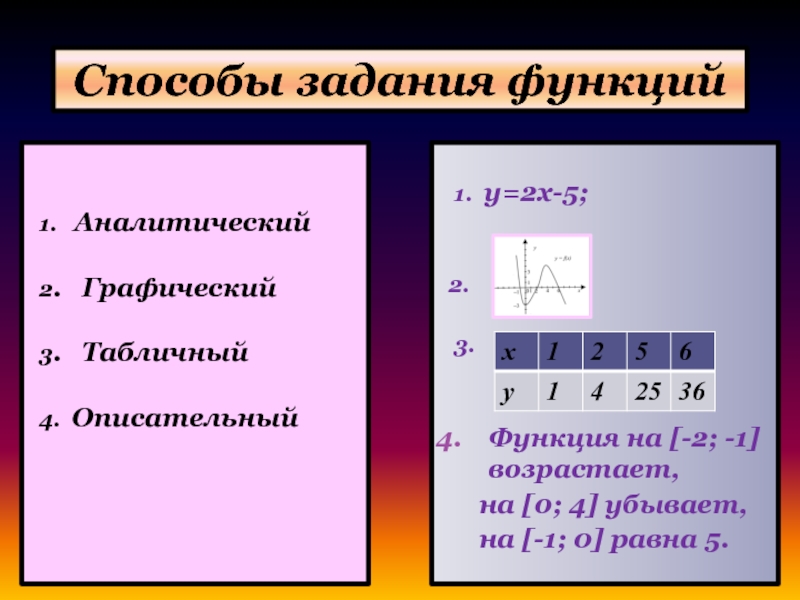
Слайд 6Способы задания функций
1. Аналитический
2. Графический
3. Табличный
4. Описательный
1. y=2x-5;
2.
3.
Функция на [-2; -1] возрастает,
на [0; 4] убывает,
на [-1; 0] равна 5.
Слайд 7График функции
Графиком функции
называют множество всех точек координатной плоскости,
абсциссы
которых равны значениям аргумента,
а ординаты- соответствующим значениям функции.
Слайд 9Свойства функций
1. Чётность:
Свойство графика
Функция называется чётной если:
D(y) симметрична относительно
0,
для любого х из D(y) выполняется условие f(x)= f(-x)
График
чётной функции симметричен относительно
оси ординат.
Слайд 10Свойства функций
Нечётность
Свойство графика
Функция называется
нечётной если
D(y) симметрична относительно
0,
для любого х из D(y) выполняется условие
f(-x)=
-f(x)График нечётной функции
симметричен относительно начала координат.
Слайд 11Свойства функций
Монотонность
Свойство графика
Функция возрастает
[или убывает] на промежутке I, если для
любого х Є I выполняется условие :
при х1>х2
f(х1)>f(х2) [при х1>х2 f(х1)
Слайд 12Свойства функций
Знакопостоянство
Свойство графика
Промежутки, на которых функция сохраняет постоянный знак, называются
промежутками знакопостоянства
+
+-
-
-
Слайд 13Графи к функции
Функция у:
Область определения – D(y)= [ - 4;
8].
Область значений – E(y)= [- 2; 5].
х
у
-2
4
0
3
7
y
D(y)
E(y)
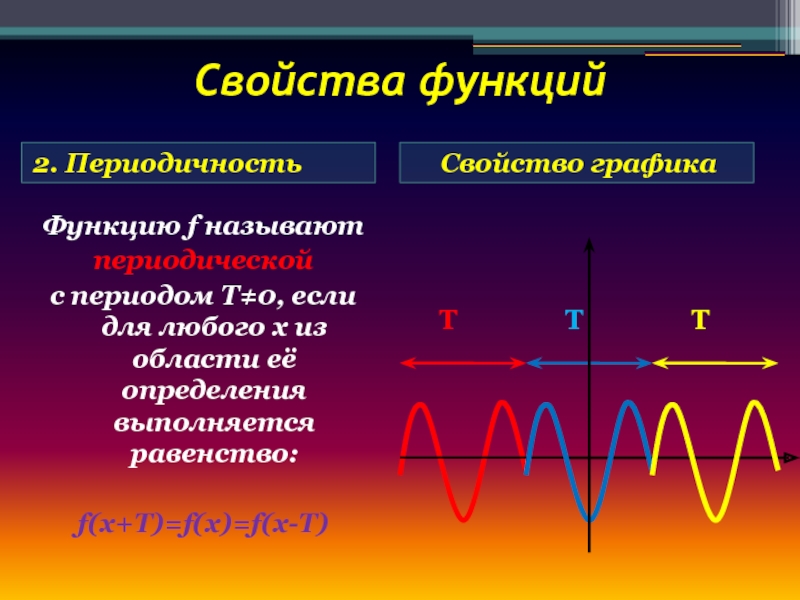
Слайд 14Свойства функций
2. Периодичность
Свойство графика
Функцию f называют
периодической
с периодом Т≠0,
если для любого х из области её определения выполняется равенство:
f(x+T)=f(x)=f(x-T)
Т
Т
Т
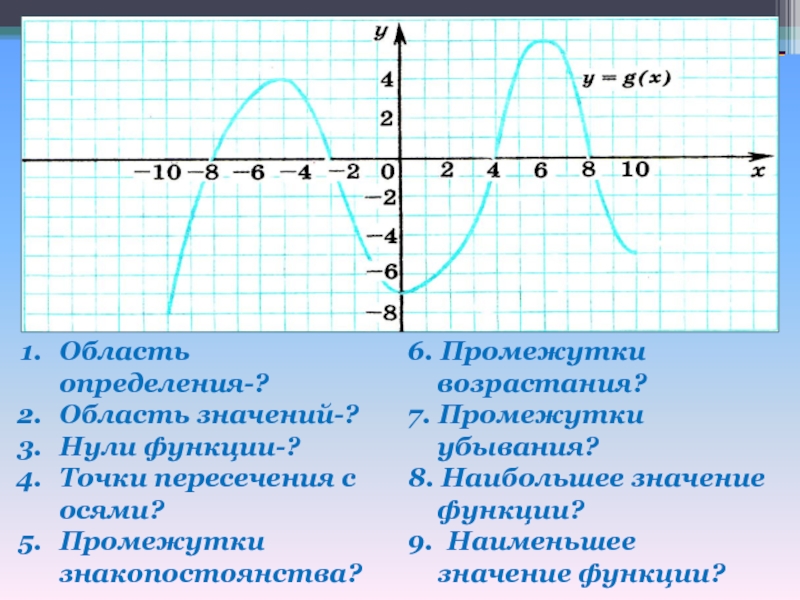
Слайд 15Область определения-?
Область значений-?
Нули функции-?
Точки пересечения с осями?
Промежутки знакопостоянства?
6. Промежутки возрастания?
7. Промежутки убывания?
8. Наибольшее значение функции?
9. Наименьшее значение функции?








![Функция Свойства функцийМонотонностьСвойство графикаФункция возрастает[или убывает] на промежутке I, если для любого Свойства функцийМонотонностьСвойство графикаФункция возрастает[или убывает] на промежутке I, если для любого х Є I выполняется условие :при](/img/thumbs/3b70ad85d3a8d3d6b0aa4da6ae0b1f61-800x.jpg)

![Функция Графи к функцииФункция у:Область определения – D(y)= [ - 4; 8].Область Графи к функцииФункция у:Область определения – D(y)= [ - 4; 8].Область значений – E(y)= [- 2; 5].ху-24037yD(y)E(y)](/img/thumbs/daf129432e656c5040888e4c0638feb8-800x.jpg)