Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Геометриялық прогрессия" тақырыбына презентация
Содержание
- 1. "Геометриялық прогрессия" тақырыбына презентация
- 2. Тақырып бойынша берілген анықтама мен ережелерді қайталауТақырып
- 3. Ауызша жұмыс Тізбектің қай түріне жататынын
- 4. Тексерейік1.Өспелі тізбек2.Кемімелі тізбек3.Монтонды тізбек4.Формула арқылы тізбек5.Графиктік тәсіл тізбегі6.Рекурренттік тәсіл тізбегі
- 5. Формуланы тап
- 6. Арифметикалық прогрессияның алғашқы
- 7. Слайд 7
- 8. Сабақтың тақырыбы: Геометриялық прогрессия
- 9. 1,2,4,8,...;
- 10. b1 =0 ал
- 11. Геометриялық прогрессия екі шартпен анықталады.1) b1=
- 12. b2=b1·q;b3=b2·q=(b1·q)·q=b1 · q²b4=b3·q=(b1· q²)·q=b1 ·
- 13. Мысалы: 1-мысал. b1=81,q=1/3 , b7=?b7=81* (1/3)7-1= 81*
- 14. Ал енді жаттығулар орындаймыз. №265,266,267
- 15. №265 b1=5, q=2;b1 =36, q= -1,2;b1 =-18,
- 16. №265 шешуі:1)b2= b1·q =5· 2 = 10;
- 17. №2661)3,12,...; 2)18, 6,....; 3)8,-16,....;q =? , b5=?
- 18. Шешуі:1)q =12:3=4 , b5=3· 256=
- 19. Деңгейлік тапсырмалар
- 20. “4”Бер-ні: Табу керек: b2,
- 21. “4”“3”b5=128*1/16=8b5=8b8:b6=q²q= √4 ,q=2 b1=96:32b1 =3Тексеру:Шешуі:
- 22. Математика тарихынан
- 23. Ал, сен білесің бе?Прогрессия термині латын тілінің
- 24. ҚорытындыФормулалармен анықтамаларды қайталадықГеометриялық прогрессияның n мүшесінің формуласын игердікҚызықты тарихи жағдайлармен таныстық
- 25. Біздің бағамыз
- 26. Рефлексия.Тест.Өзімнің жеке жұмысым бойынша ...А.Тақырып бойынша түсіндім.В.Есеп
- 27. Үйге тапсырма №268, №270
- 28. Осымен сабағымыз аяқталды ,рахмет.
- 29. Скачать презентанцию
Тақырып бойынша берілген анықтама мен ережелерді қайталауТақырып бойынша алған білімдерін бекітуЕсеп шығаруда формулаларды пайдалана білуін байқауЕсептеу қабылетін ,пәнге деген қызығушылығын нығайтуОқушылардың өз бетінше жұмыс істеу дағдысын қалыптастыруСабақтың мақсаты :
Слайды и текст этой презентации
Слайд 2Тақырып бойынша берілген анықтама мен ережелерді қайталау
Тақырып бойынша алған білімдерін
бекіту
Есеп шығаруда формулаларды пайдалана білуін байқау
Есептеу қабылетін ,пәнге деген қызығушылығын
нығайтуОқушылардың өз бетінше жұмыс істеу дағдысын қалыптастыру
Сабақтың мақсаты :
Слайд 3
Ауызша жұмыс
Тізбектің қай түріне
жататынын анықта
1)5; 5,5; 6; 6,5…..
2)-9;
-10,5; -12; -13,5…..
3)-2,2; 4,4; -8,8; 17,6…..
4) аn=3n-2,an=5n,an=4n+6...
5) Y1=-2,y2=-1,y3=0,y4=1,y5=2,y6=3,...
6) 0,0,0,....:3,3,3,...:а,а,а,.....:
Слайд 4Тексерейік
1.Өспелі тізбек
2.Кемімелі тізбек
3.Монтонды тізбек
4.Формула арқылы тізбек
5.Графиктік тәсіл тізбегі
6.Рекурренттік тәсіл тізбегі
Слайд 6 Арифметикалық прогрессияның алғашқы n –ші мүшесінің қосындысының формуласы Арифметикалық
прогрессияның
айырымының формуласы
Арифметикалық прогрессияның
анықтамасы
Арифметикалық прогрессияның
n-ші мүшесінің формуласы
Арифметикалық прогрессияның
кезкелген мұшесін анықтайтын формула
Слайд 7
Арифметикалық прогрессияның
анықтамасы
Арифметикалық прогрессияның
n-ші мүшесінің формуласы
Арифметикалық прогрессияның
кезкелген мұшесін анықтайтын формула
Арифметикалық прогрессияның айырымының формуласы
Арифметикалық прогрессияның алғашқы
n –ші мүшесінің қосындысының формуласы
Слайд 91,2,4,8,...;
5,25,125,625,...;
3) 0,2, -0,6,
1,8, -5,4, 16,2,...;
4) 1, -1/2, 1/4, -1/8,...
.Осы мысалдардың барлығында ортақ ерекшелік бар:Тізбектің екінші мүшесінен бастап әрбір мүшесі өзінің алдыңғы мүшесін бір тұрақты санға көбейтуден шығып отырады.
Слайд 10 b1 =0 ал b2 - ден
бастап кезкелген мүшесі өзінің алдындағы мүшені нөлден өзгеше тұрақты санға
көбейткенде шығатын сандық тізбек геометриялық прогрессия деп аталады. 1-4 мысалдардың бәрі геометриялық прогрессия болады,олардың еселіктері 2-ге;5-ке;-1/2-ге және -3-ке тең. Мүшелері тұрақты бір ғана сан болатын 4,4,4,...тізбегін,еселігі q=1болатын геометриялық прогрессия деп қарастыруға болады.Мұндай геометриялық прогрессия тұрақты деп аталады. Геометриялық прогрессияның анықтамасынан оның кез келген қатарлас екі мүшесінің қатнасы тұрақты екені шығады,яғни: b2:b1=b3:b2=.... =bn+1:bn=q. q- дегеніміз еселікСлайд 11Геометриялық прогрессия екі
шартпен анықталады.
1) b1= b ( b≠ 0);
2) b n+1 = q · b
n ;( q≠0 )
Геометриялық прогрессия берілу үшін оның біріншісі мүшесі - b 1 және еселігі- q берілу керек.
Мысалы: 1) 8, -16, 32, -64 ,128,....;
b1= 8>0 , q = - 2 < 0 оң ,теріс пргрессия ,
2) -3 ,-6, -12 , .... b1 =-3 , q=2 ,b1 < 0, q>0 болса ,теріс прогрессия,
3) 3,6,12,24,... егер b1>0 , q>0 болса , онда мүшелері оң болатын геометриялық прогрессия шығады
Слайд 12
b2=b1·q;
b3=b2·q=(b1·q)·q=b1 · q²
b4=b3·q=(b1· q²)·q=b1 · q³
......................................
bn=b n-1 ·q=...=b1·
qn-1
bn=b1· qn-1
Геометриялық пргрессиягың
кез келген мүшесінің формуласы.
Слайд 13Мысалы:
1-мысал. b1=81,q=1/3 , b7=?
b7=81* (1/3)7-1= 81* (1/3)6=81/729=1/9
b7= 1/9
2-мысал. 2/3, 2,6,
18, 54 ,.... bn =?
2:2/3=q, q=3, bn =b1 · qn-1
= 2/3 ·3n-1=2 · 3n-2 bn = 2 · 3n-2
3-мысал .1/16 саны 16,8,4,... n = ?
b1=16, q=1/2, 1/16 =16 ·(1/2) n-1, (1/2)8 = (1/2) n-1,
n-1 =8, n = 9. b9=1/16
Слайд 16№265 шешуі:
1)b2= b1·q =5· 2 = 10;
b3 = b1·q2
=5· 4 = 20
b4 = b1·q3 =5· 8=40
2) b1
=36, q= -1,2; b2= - 43,2 , b3 =-51,84, b4=62,2083)b1 =-18, q=1/3; b2=-6, b3 =-2, b4=-2/3
Слайд 20
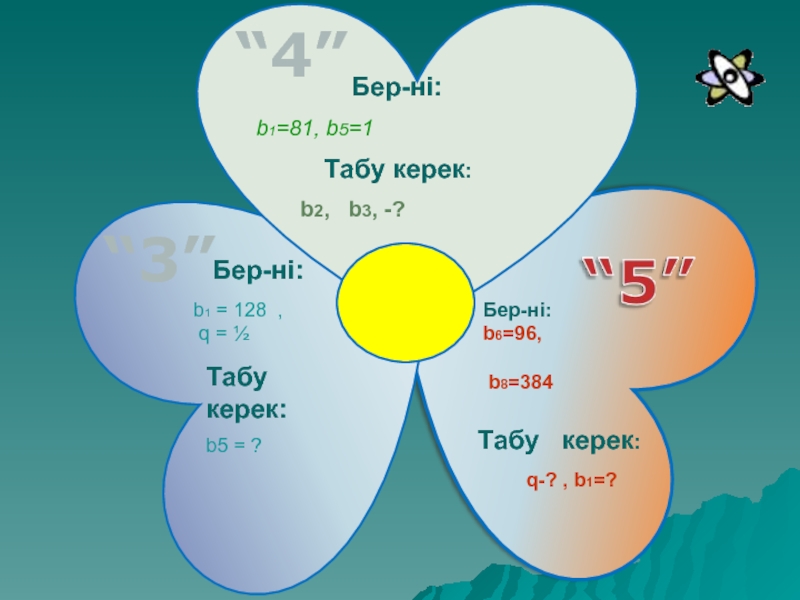
“4”
Бер-ні:
Табу керек:
b2, b3, -?
b1=81, b5=1
Бер-ні:
Табу керек:
b5 = ?
Табу керек:
q-? , b1=?“3”
b1 = 128 ,
q = ½
Бер-ні: b6=96,
b8=384
Слайд 21
“4”
“3”
b5=128*1/16=8
b5=8
b8:b6=q²
q= √4 ,q=2
b1=96:32
b1 =3
Тексеру:
Шешуі:
b1=81, b5=1
b2-? ,b3-?b5:b1=q
q=1/3, b2=b1*q=81*1/3=27,
b3=b1*q²=81*(1/3) ²=9
Слайд 23Ал, сен білесің бе?
Прогрессия термині латын тілінің прогиесио деген сөзінен
шыққан,мағнасы –ілгері жүру.Бұл атауды алғаш рет Рим математигі Аник Боэций
қолданған.Прогрессиялар мен тізбектер жөніндегі ілімнің алғашқы нышаны мысырлықтар мен вавилондықтардан басталады.Мысырлықтардың папирус жапырақтарына жазған есептерінің кейбіреуі прогрессиянық есептері болып табылады.Мысалы,” 10 өлшем арпаны 10 адамға бөліп бер,әр адамға тиетін арпа өлшемінің бір-бірінен айырымы 1/8 болсын.”Бұл –айырымы d=1/8 болатын арифметикалық прогрессия.Папируста 1-адамның үлесін табатын ереже келтірілген.Мысырлықтар бұл ережені қалай тапқаны белгісіз.
Слайд 24Қорытынды
Формулалармен анықтамаларды қайталадық
Геометриялық прогрессияның n мүшесінің формуласын игердік
Қызықты тарихи жағдайлармен
таныстық
Слайд 26Рефлексия.
Тест.
Өзімнің жеке жұмысым бойынша ...
А.Тақырып бойынша түсіндім.
В.Есеп шығарып үйрендім.
С.Бүкіл өткен
тақырыпты қайталадым.
Сізге сабақ уақытысында есеп шығару үшін не кедергі болды?
А.Білімім. Б. Уақыт. С.Тілек. Д.Есепті шығардым.
Сабақ уақтысында қыйыншылықтарды жеңуге кім көмек берді? А.Сыныптастарым. Б.Мұғалім.
С.Оқулық. Д.Ешкім.