Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графический способ решения систем уравнений
Содержание
- 1. Графический способ решения систем уравнений
- 2. Графический способ решения систем уравнений111
- 3. Цель :научиться решать системы уравнений с двумя переменными графическим способом
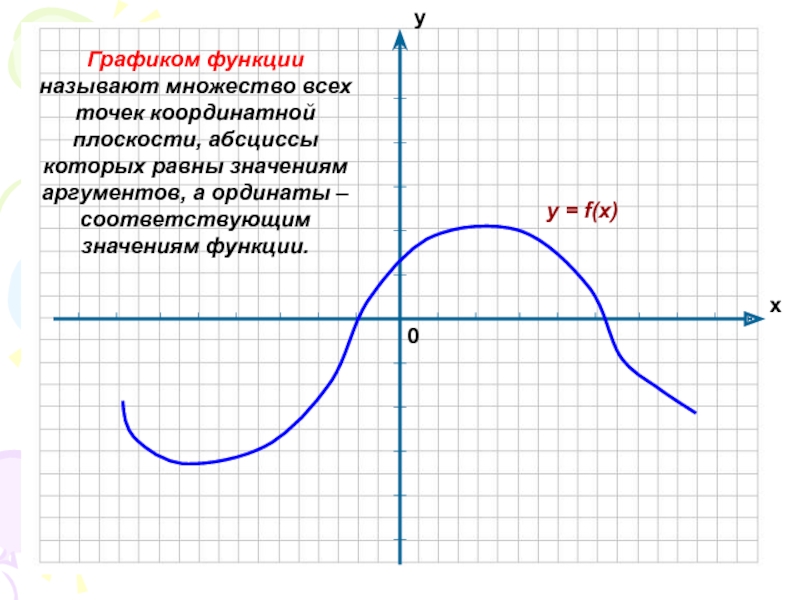
- 4. Графиком функции называют множество всех точек координатной
- 5. График - прямая11
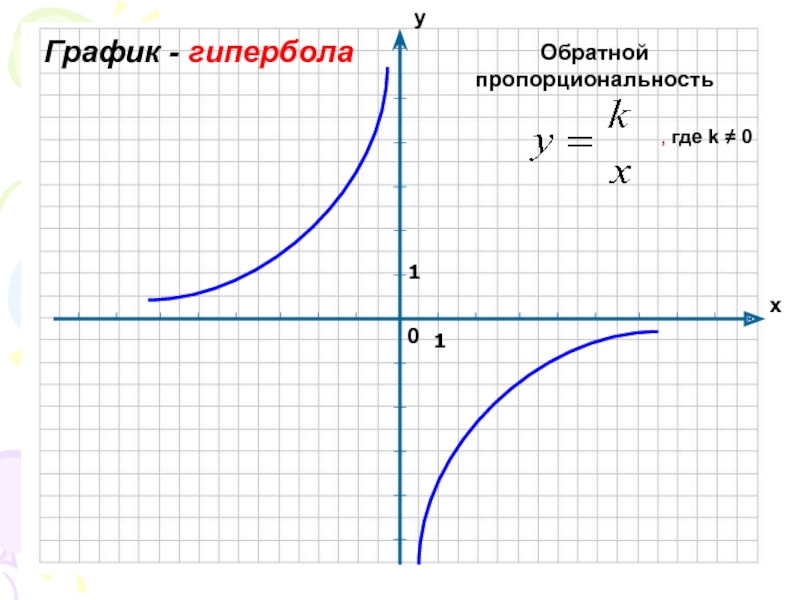
- 6. График - гипербола11
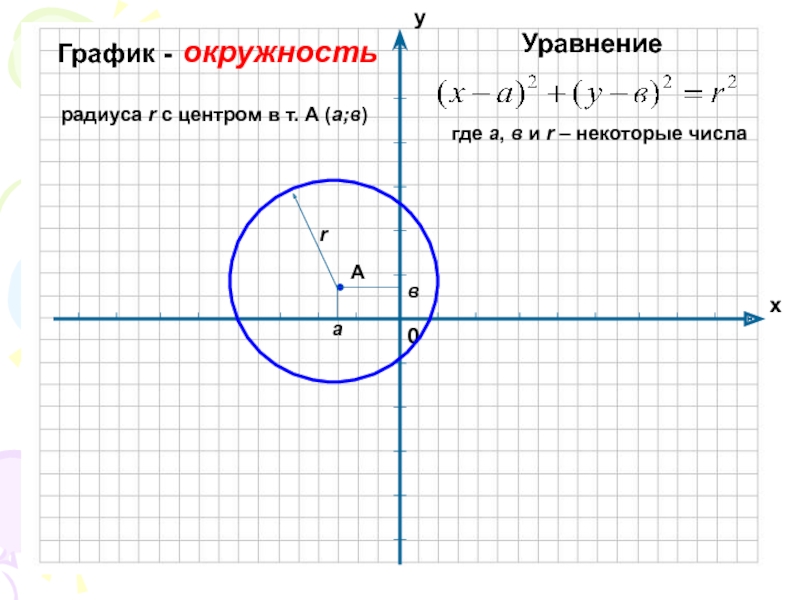
- 7. Слайд 7
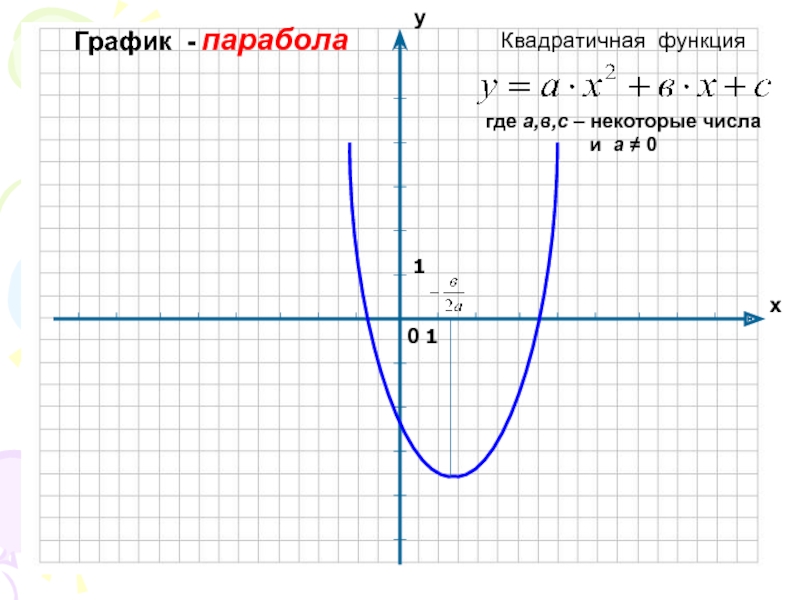
- 8. График - парабола11
- 9. Графиком уравнения с двумя переменными называетсямножество
- 10. График - строфоидахУравнение11
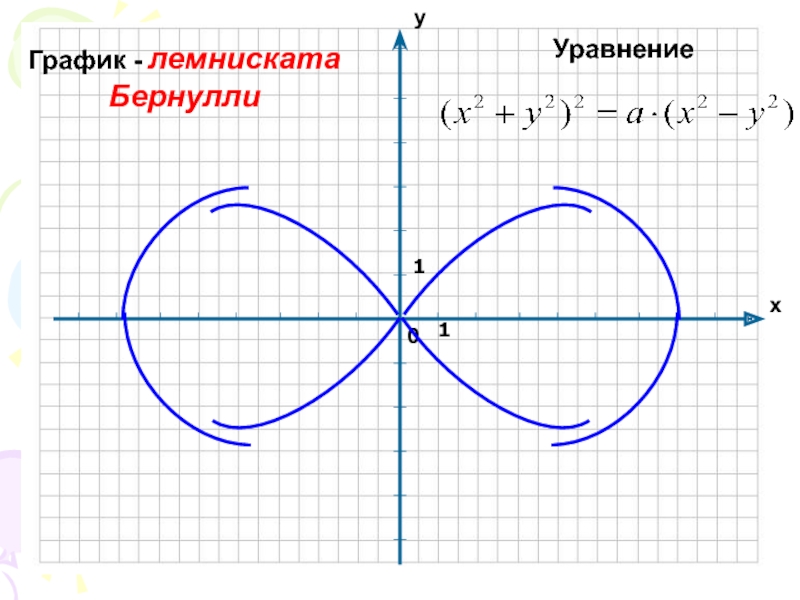
- 11. График - лемниската Бернулли11
- 12. График - астроида
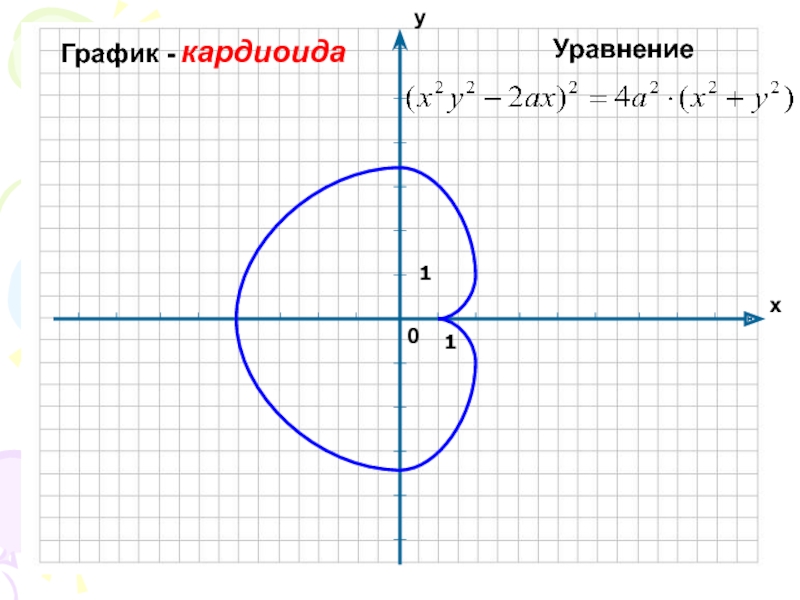
- 13. График - кардиоида11
- 14. Построим в одной системе координат графики уравненийх2
- 15. Чтобы решить систему уравнений с двумя неизвестными,
- 16. 1)Если точек пересечения графиков нет
- 17. 1У=3х
- 18. 11Решить систему -4х+1---------------------------------------------------------------------------------------2-3У=Х-3{ -4х+1У=Х-32
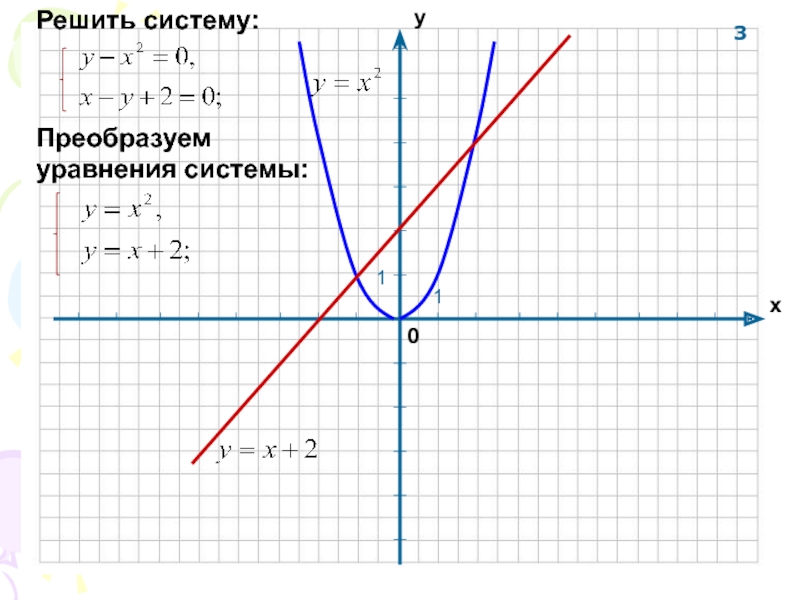
- 19. 3
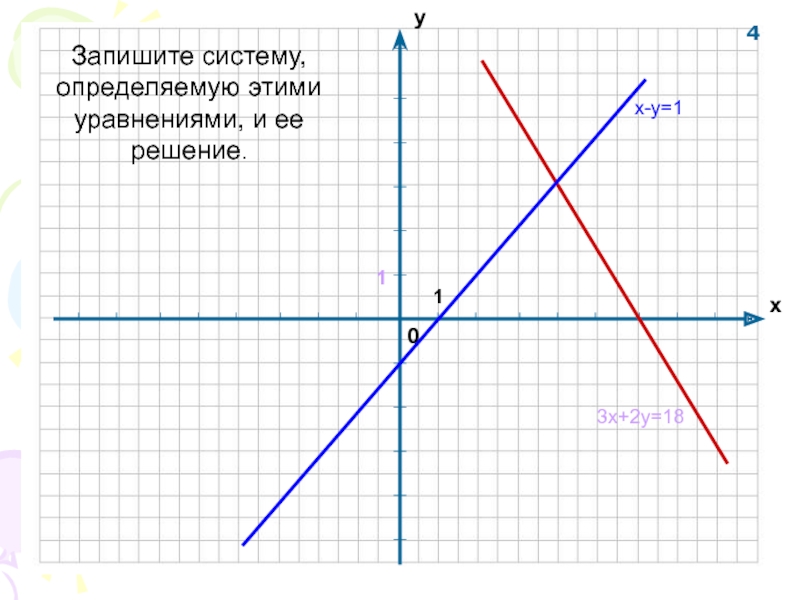
- 20. 3х+2у=18Запишите систему, определяемую этими уравнениями, и ее решение.4
- 21. 5
- 22. 6
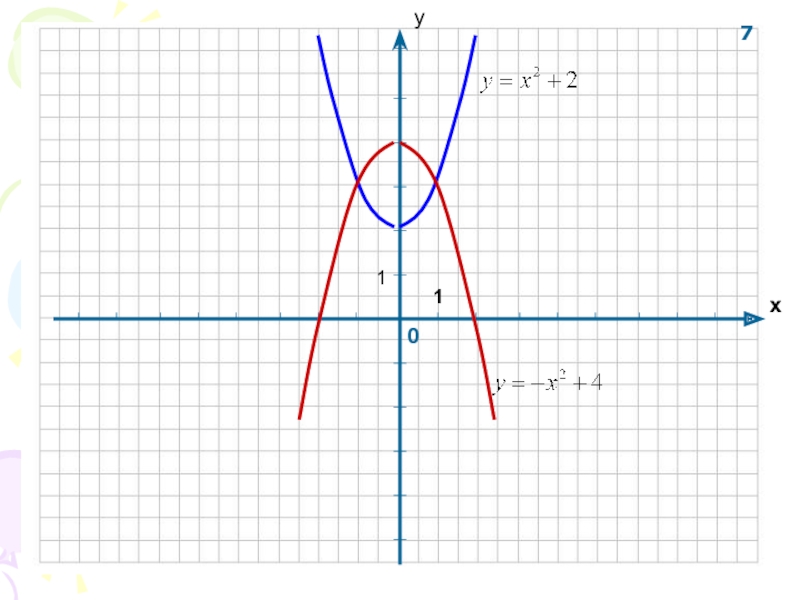
- 23. 7
- 24. СПАСИБО ЗА УРОК
- 25. Скачать презентанцию
Графический способ решения систем уравнений111
Слайды и текст этой презентации
Слайд 4Графиком функции называют множество всех точек координатной плоскости, абсциссы которых
равны значениям аргументов, а ординаты – соответствующим значениям функции.
у =
f(х)Слайд 9
Графиком уравнения
с двумя переменными называется
множество точек координатной плоскости,
координаты
которых обращают
уравнение в верное равенство.
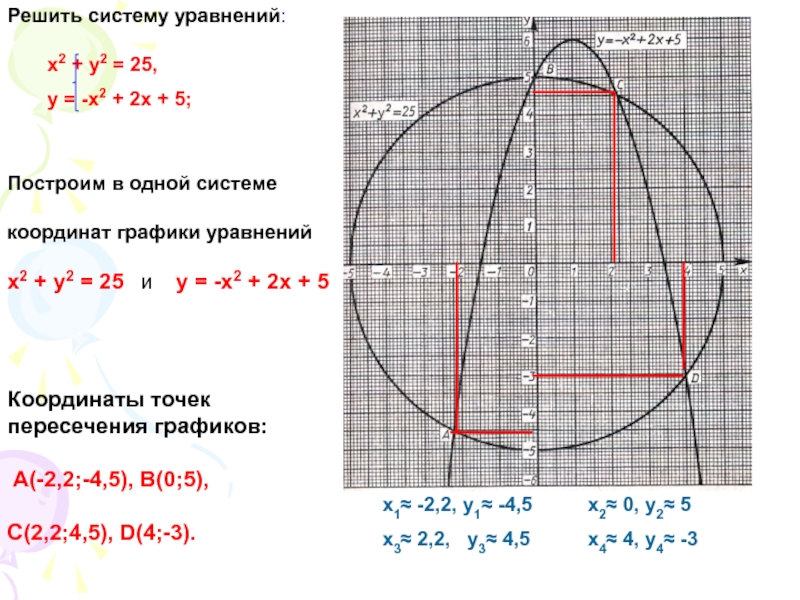
Слайд 14Построим в одной системе
координат графики уравнений
х2 + у2 =
25 и у = -х2 + 2х +
5Координаты точек
пересечения графиков:
А(-2,2;-4,5), В(0;5),
С(2,2;4,5), D(4;-3).
х1≈ -2,2, у1≈ -4,5 х2≈ 0, у2≈ 5
х3≈ 2,2, у3≈ 4,5 х4≈ 4, у4≈ -3
.
Слайд 15
Чтобы решить систему уравнений с двумя неизвестными, нужно :
1)Построить в одной системе координат графики уравнений, входящих в систему;
2)Найти точки пересечения графиков;3) Определить координаты этих точек (если они есть) ;
4)Записать ответ.
Алгоритм :
Слайд 16 1)Если точек пересечения графиков нет , то система
решений
не имеет;
2) Чтобы проверить точность полученных решений,
их нужно подставить
в уравнение системы и сделать проверку.
3)Если графики совпадут, то система имеет
множество решений
ЗАМЕЧАНИЕ :