Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратный трехчлен
Содержание
- 1. Квадратный трехчлен
- 2. Квадратный трехчлен-Выражение вида ax²+bx+c, где а≠0
- 3. Квадратное уравнениеax²+bx+c=0, где а≠0
- 4. Квадратный трехчленКорень квадратного трёхчлена — это значение переменной х , обращающее квадратный трёхчлен в ноль.
- 5. Квадратный трехчленКоэффициенты квадратного трехчлена имеют собственные названия:
- 6. Дискриминант-Выражение вида D=b²-4acD-число В зависимости от
- 7. Квадратный трехчленЕсли D>O, то квадратный трехчлен можно
- 8. Квадратный трехчленПример. x²-4x+3, a=1, b= -
- 9. Квадратный трехчленЕсли D=O, то квадратный трехчлен можно
- 10. Квадратный трехчленПример: 4x² - 4x +1,
- 11. Квадратный трехчлен Если D
- 12. Квадратный трехчленПример: x²+6x+10, где a=1, b=6, c=10 D= 6² - 4·1·10 = 36-40 = -4
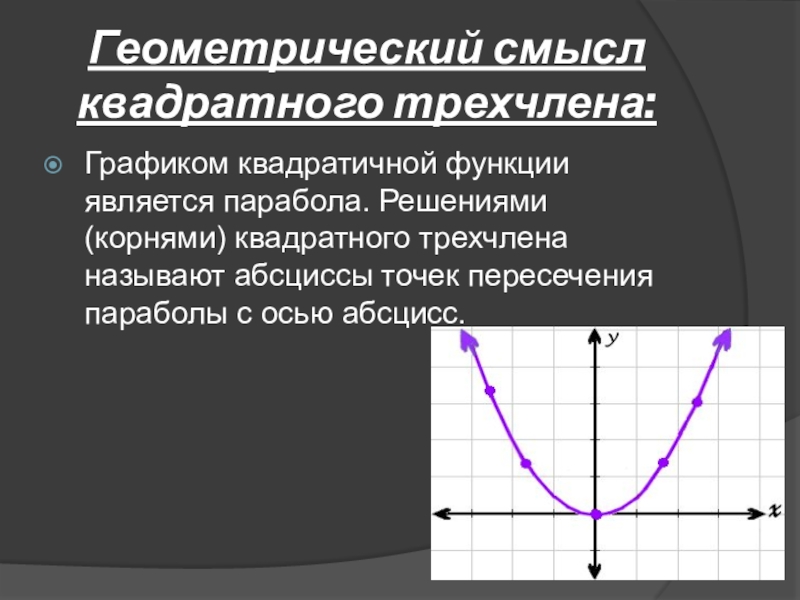
- 13. Геометрический смысл квадратного трехчлена:Графиком квадратичной функции является
- 14. СПАСИБО ЗА ВНИМАНИЕ!!!
- 15. Скачать презентанцию
Квадратный трехчлен-Выражение вида ax²+bx+c, где а≠0
Слайды и текст этой презентации
Слайд 4Квадратный трехчлен
Корень квадратного трёхчлена — это значение переменной х ,
обращающее квадратный трёхчлен в ноль.
Слайд 5Квадратный трехчлен
Коэффициенты квадратного трехчлена имеют собственные названия: коэффициент а называют
первым или старшим, коэффициент b называют вторым или коэффициентом при
x , c называется свободным членом.
Слайд 6Дискриминант-
Выражение вида
D=b²-4ac
D-число
В зависимости от знака D квадратный
трёхчлен имеет либо 2 различных корня х₁ и х₂, либо
2 одинаковых корня х₁= х₂ (будем говорить один корень), либо не имеет корней (в области действительных чисел)
Слайд 7Квадратный трехчлен
Если D>O, то квадратный трехчлен можно разложить на множители:
ax²+bx+c=a(x-x₁)(x-x₂), где
х₁ = (-b+√D)/(2a),
х₂
= (-b-√D)/(2a)
Слайд 8Квадратный трехчлен
Пример.
x²-4x+3, a=1, b= - 4, c=3
D= (-
4)² - 4· 1· 3=16 - 12= 4>0
Квадратный
трехчлен имеет 2 различных действительных корня:х₁ = (-(-4)+√4)/(2·1) = (4+2)/ 2 = 3
х₂ = (-(-4)-√4)/(2·1) = (4-2)/2 = 1
x²-4x+3 = (x – 3)· (x - 1)
Слайд 9Квадратный трехчлен
Если D=O, то квадратный трехчлен можно разложить на множители:
ax²+bx+c=a(x-x₁)², где
x₁ = -b/(2a)
Слайд 10Квадратный трехчлен
Пример:
4x² - 4x +1, где a =
4, b = -4, c = 1
D =
(-4)² - 4·4·1 = 16-16 = 0Квадратный трехчлен имеет 2 одинаковых действительных корня х₁ = х₂ (будем говорить один корень)
х₁ = -(-4)/(2·4) = 4/8 = ½
4x² - 4x +1 = 4(x-1/2)²
Слайд 12Квадратный трехчлен
Пример:
x²+6x+10, где a=1, b=6, c=10
D= 6² -
4·1·10 = 36-40 = -4
действительных корней, следовательно его нельзя разложить на множители
Слайд 13Геометрический смысл квадратного трехчлена:
Графиком квадратичной функции является парабола. Решениями (корнями)
квадратного трехчлена называют абсциссы точек пересечения параболы с осью абсцисс.
