отрезке
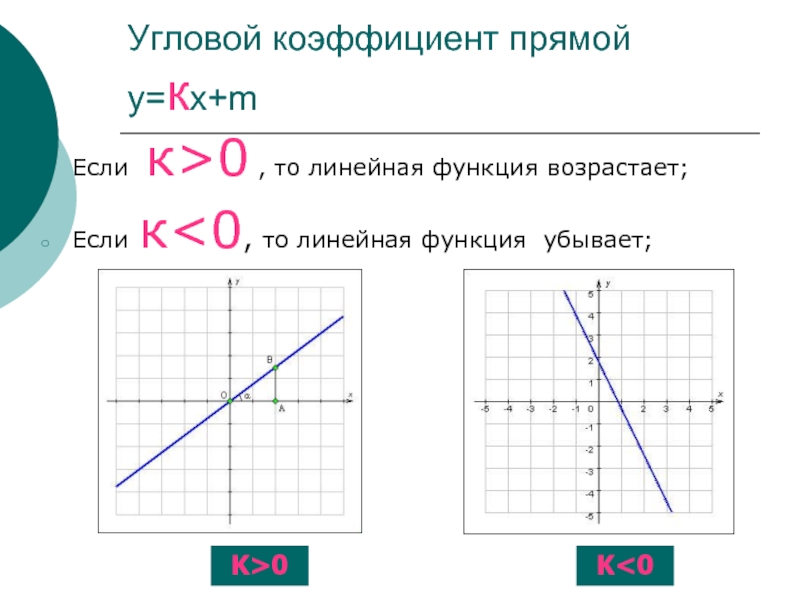
Угловой коэффициент прямой
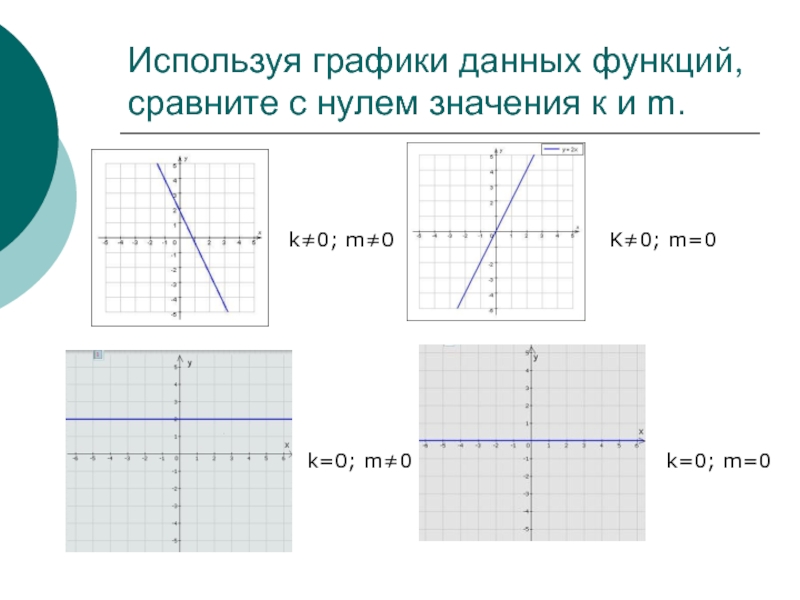
Зависимость расположения графика от коэффициентов
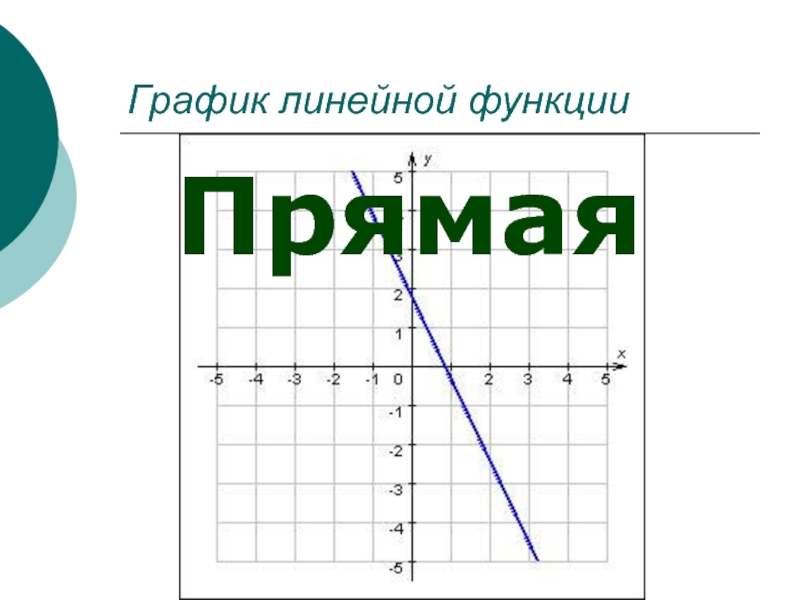
Прямая пропорциональность
Физминутка
Взаимное расположение графиков
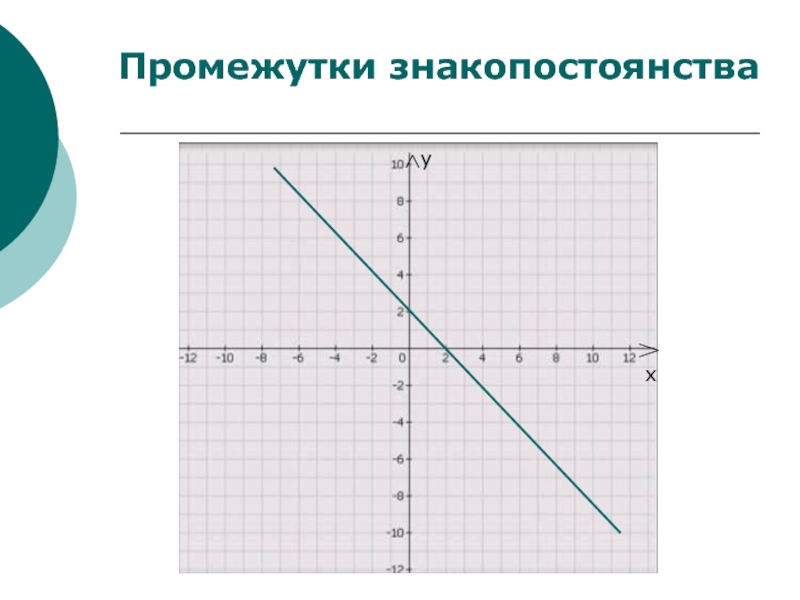
линейных функцийПромежутки знакопостоянства
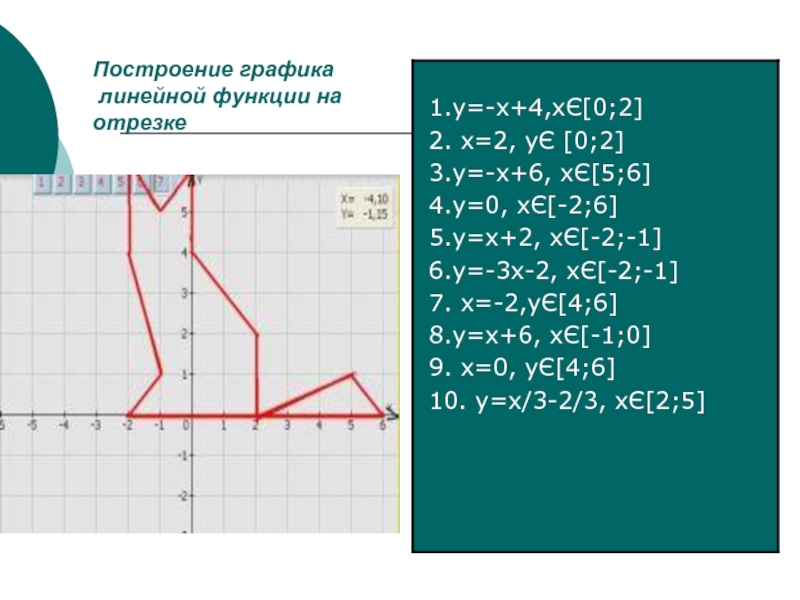
Построение графика линейной функции на отрезке
Домашнее задание
Содержание










![Линейная функция Домашнее заданиеПостроить отрезки в одной системе координат. 1. у=-2, Домашнее заданиеПостроить отрезки в одной системе координат. 1. у=-2, хЄ[-4;-2] 2.](/img/thumbs/580037f4a64e80334067c1d2f88b0451-800x.jpg)



















