Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика на шахматной доске
Содержание
- 1. Математика на шахматной доске
- 2. Цель: найти и разобрать
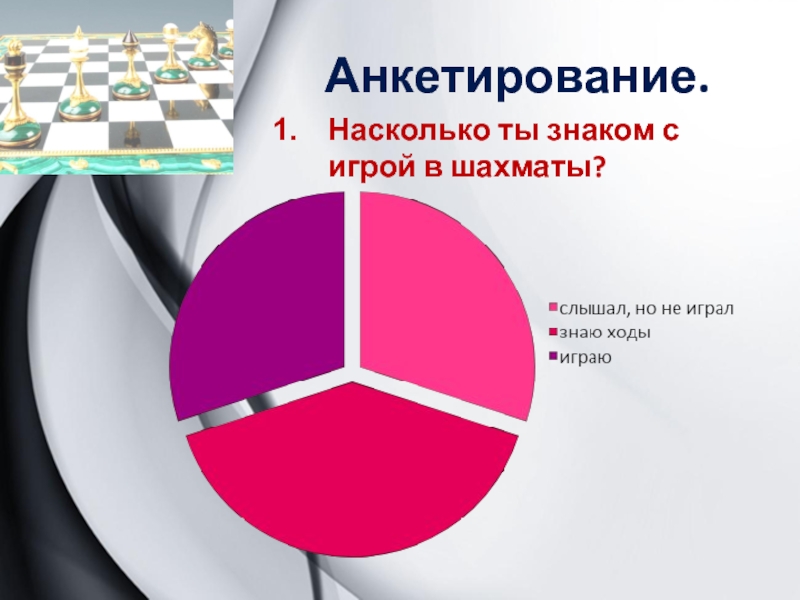
- 3. Анкетирование.Насколько ты знаком с игрой в шахматы?
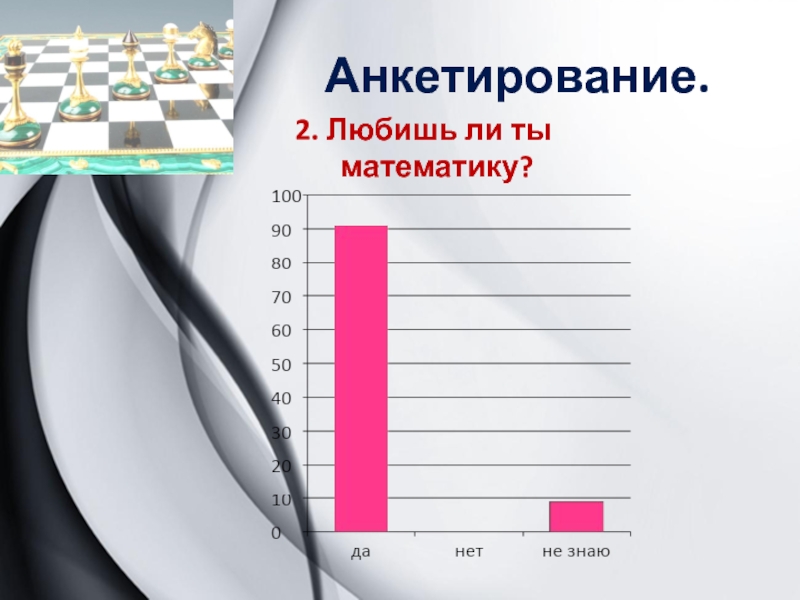
- 4. Анкетирование.2. Любишь ли ты математику?
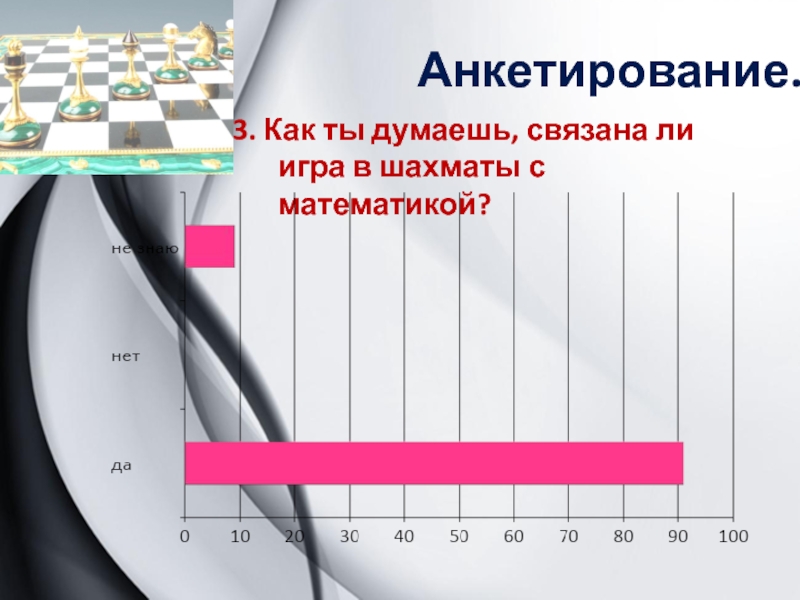
- 5. Анкетирование.3. Как ты думаешь, связана ли игра в шахматы с математикой?
- 6. Историческая справка: Шахматная игра была
- 7. Математика на шахматной доске
- 8. Симметрия
- 9. Система координат Система координат
- 10. Чётность и нечётностьПри каждом ходе король меняет
- 11. Геометрия шахматной доски Исход
- 12. Задачи на шахматной доске
- 13. Решение: Вы, наверное, заметили, что, делая каждый
- 14. Задача Один восточный
- 15. Задача На
- 16. Шахматная
- 17. СПАСИБО ЗА ВНИМАНИЕ!
- 18. Скачать презентанцию
Цель: найти и разобрать связь между шахматами и математикой, воспользоваться этой связью при решении математических задач. Объект исследования - Шахматная доска Предмет исследования – математические задачи, связанные с шахматной
Слайды и текст этой презентации
Слайд 1Математика на
шахматной доске
Выполнила: Медунова Татьяна
Ученица 6 «Б» класса
Руководитель: Лузан Е.В.
Пенза 2016
Слайд 2 Цель: найти и разобрать связь между шахматами
и математикой, воспользоваться этой связью при решении математических задач.
Объект исследования
- Шахматная доска Предмет исследования – математические задачи, связанные с шахматной доской и шахматными фигурами.
Слайд 6Историческая справка:
Шахматная игра была придумана в Индии,
и когда индусский царь Шерам познакомился с нею, он был
восхищён её остроумием и разнообразием возможных в ней положений.Слайд 9Система координат
Система координат используется и в
шахматах. Горизонтали (Ох) на шахматной доске обозначаются латинскими буквами, а
вертикали (Оу) – цифрамиСлайд 10Чётность и нечётность
При каждом ходе король меняет четность хода. Например,
первый ход – нечётный, второй – чётный и т.д. Одновременно
с этим король меняет цвет клетки, на которой он стоит.Слайд 11Геометрия шахматной доски
Исход партии можно оценить
при помощи «правила квадрата».
Достаточно выяснить, может ли король при своем ходе попасть в квадрат пешки. Итак, в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.Слайд 12Задачи на шахматной доске
Задача: Конь вышел
на поле А8 и через несколько ходов вернулся на него.
Докажите, что он сделал чётное число ходов.Слайд 13Решение:
Вы, наверное, заметили, что, делая каждый ход, конь меняет
цвет клетки на которой он стоит.
Следовательно:
каждый нечетный ход конь будет вставать на чёрную клетку. Исходя из этого и зная то, что конь должен вернуться на клетку А8, белого цвета, мы можем сказать, что он вернется через четное число ходов.Слайд 14Задача
Один восточный властелин был таким
искусным игроком, что за всю жизнь потерпел всего четыре поражения.
В честь своих победителей, четырех мудрецов, он приказал вставить в его шахматную доску четыре алмаза — на те поля, на которых был заматован его король (см. рис. где вместо алмазов изображены кони).Слайд 15Задача
На какое максимальное число
разных частей можно разрезать шахматную доску, если считать разными части,
отличающиеся своей формой или цветом полей при совмещении. Переворачивать части не разрешается. Максимальное число частей равно 18. На рис. 3 представлены два вида разрезов.Слайд 16 Шахматная математика — один
из самых популярных жанров занимательной математики, логических игр и развлечений.
В ходе работы я постаралась исследовать связь математики и шахмат, рассмотрела математические решения задач, связанных с шахматной доской и шахматными фигурами.