Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по математике на тему : "Звездный час"
Содержание
- 1. Презентация по математике на тему : "Звездный час"
- 2. «Предмет математики настолько серьезен, что не следует
- 3. Дерзайте, играйте и выигрывайте!
- 4. I тур 1 задание
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. I тур 2 задание
- 13. 1
- 14. 1
- 15. 1
- 16. 1
- 17. I тур 3 задание
- 18. 1
- 19. 1
- 20. 1
- 21. I тур 4 задание
- 22. у= х6
- 23. II тур 1 задание
- 24. Пифагор
- 25. Пифагор
- 26. Слайд 26
- 27. Пифагор
- 28. Пифагор
- 29. Пифагор
- 30. II тур 2 задание
- 31. 1) у = - х2 –
- 32. 1) у = - х2 –
- 33. 1) у = - х2 –
- 34. 1) у = - х2 –
- 35. II тур 3 задание
- 36. Слайд 36
- 37. Слайд 37
- 38. II тур 4 задание
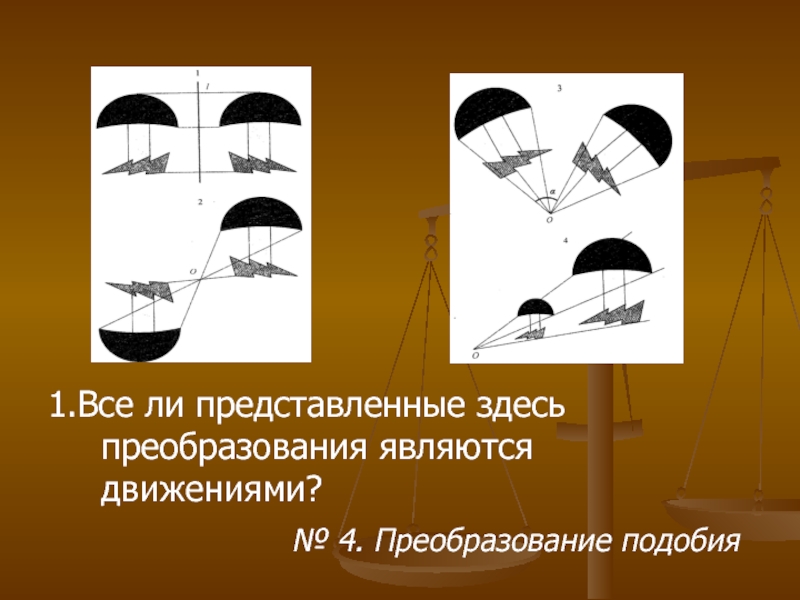
- 39. 1.Все ли представленные здесь преобразования являются движениями?
- 40. II тур 5 задание
- 41. Карлсон попросил у Малыша малинового варенья.На полке
- 42. III тур 1 задание
- 43. Слайд 43
- 44. Слайд 44
- 45. 1
- 46. III тур 2 задание
- 47. 1. у = 3х2 – 2х5 +
- 48. 1. у = 3х2 – 2х5 +
- 49. 1. у = 3х2 – 2х5 +
- 50. III тур 3 задание
- 51. 1
- 52. III тур 4 задание
- 53. 1
- 54. 1
- 55. 1
- 56. III тур 5 задание
- 57. 1. S = ½ ab sin
- 58. IV тур 1 задание
- 59. Аукционматематическихтерминов
- 60. Финал
- 61. АРИФМЕТИКА
- 62. Звездный час
- 63. Спасибо за игру!
- 64. Скачать презентанцию
«Предмет математики настолько серьезен, что не следует упускать ни одной возможности сделать его более занимательным» Блез Паскаль
Слайды и текст этой презентации
Слайд 2«Предмет математики настолько серьезен, что не следует упускать ни одной
возможности сделать его более занимательным»
Блез Паскаль
Слайд 5
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
1. Кто из них является автором учебника для детей под названием «Арифметика»?
№ 1. Л. Н. Толстой
Слайд 6
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
2. С кем из них произошел следующий случай?
№ 2. М. В. Ломоносов
Слайд 7
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
3. Кто из этих знаменитых людей сделал интересное и меткое «арифметическое» сравнение, что человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель – то, что он думает о себе.
№ 1. Л. Н. Толстой
Слайд 8
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
4. Кому принадлежат слова: «Вдохновение нужно в геометрии, как и в поэзии»?
№ 3. А. С. Пушкин
Слайд 9
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
5. Кому из этих людей принадлежат следующие слова: «Математику уже затем учить следует, что она ум в порядок приводит»?
№ 2. М. В. Ломоносов
Слайд 10
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
6. Мне кажется, что фамилиями этих людей названы города. Так ли это?
№ 1. Л. Н. Толстой
Слайд 11
1
2 3Л.Н.Толстой М.В.Ломоносов А.С.Пушкин
7. По чьему проекту в 1755 году был организован Московский университет, носящий ныне его имя?
№ 2. М. В. Ломоносов
Слайд 15
1
2
3 43)Для какого четырёхугольника имеет смысл выражений «Найдите среднюю линию»?
№ 3. Трапеция.
Слайд 16
1
2
3 44) Название какой фигуры в переводе с греческого языка означает «обеденный столик»?
№ 3. Трапеция.
Слайд 18
1 2
3
41) Я утверждаю, что все они являются графиками некоторых функций. Так ли это?
№ 4. Окружность не
является графиком функции.
Слайд 20
1 2
3
43)На каком рисунке изображен график возрастающей на всей области определения функции?
№ 2
Слайд 22
у= х6 у
= х37 у = х48
у = х1001 2 3 4
Я считаю, что графики всех предложенных функций расположены в I и II координатных четвертях. Верно ли это?
№ 2. Нет, графиком второй функции
является кубическая парабола, он
расположен в I и III координатных четвертях.
Слайд 24
Пифагор
Архимед Фалес
1 2 3
1.Девизом каждого, кто нашел что-то новое, является слово «Эврика!». Так воскликнул ученый, открыв новый закон. Он с большой точностью вычислил значение π - отношение длины окружности к её диаметру.
№ 2. Архимед.
Слайд 25
Пифагор
Архимед Фалес
1 2 3
2. Кто из этих учёных участвовал в атлетических состязаниях и на олимпийских играх был дважды увенчан лавровым венком за победу в кулачном бою?
№ 1. Пифагор.
Слайд 26
Пифагор
Архимед Фалес1 2 3
3. Много интересного рассказывают про этого учёного. Вот, например, один случай. Учёный, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит».
№ 3. Фалес.
Слайд 27
Пифагор
Архимед
Фалес1 2 3
4. Кто из этих учёных помогал защищать свой город Сиракузы от римлян и при этом погиб? Легенда гласит: когда римлянин занёс меч над учёным, тот не просил пощады, а лишь воскликнул: «Не трогай мои чертежи!» В миг гибели учёный решал геометрическую задачу.
№ 2. Архимед.
Слайд 28
Пифагор
Архимед Фалес
1 2 3
5. Кому из них принадлежат слова: «Числа правят миром»?
№ 1. Пифагор.
Слайд 29
Пифагор
Архимед
Фалес1 2 3
6. Кто из этих учёных сформулировал следующие теоремы «Вертикальные углы равны», «В равнобедренном треугольнике углы при основании равны», «Диаметр делит круг пополам» и др.
№ 3. Фалес.
Слайд 31 1) у = - х2 – 7х + 3
2) у = - 1 +
3х + 7х23) у = - (х + 7)2 – 3
4) у = 3 - 7х2
1)Верно ли, что ветви всех парабол направлены вниз?
№ 2 - вверх.
Слайд 32 1) у = - х2 – 7х + 3
2) у = - 1 +
3х + 7х23) у = - (х + 7)2 – 3
4) у = 3 - 7х2
2)Вершина какой параболы находится в точке с координатами (0;3)?
№4.
Слайд 33 1) у = - х2 – 7х + 3
2) у = - 1 +
3х + 7х23) у = - (х + 7)2 – 3
4) у = 3 - 7х2
3)Осью симметрии какой параболы является прямая
х = —7
№3.
Слайд 34 1) у = - х2 – 7х + 3
2) у = - 1 +
3х + 7х23) у = - (х + 7)2 – 3
4) у = 3 - 7х2
4)Какую из парабол можно получить из графика функции у = х2 с помощью двух параллельных переносов: вдоль оси абсцисс на 7 ед. отр. влево и вдоль оси ординат на 3 ед. отр. вниз?
№3.
Слайд 36 1
2
Локоть Дюйм
3 4
Фут Фунт
1)Локоть, дюйм, фут, фунт – по-моему, это единицы измерения длины. Так ли это?
№ 4. Фунт – это мера веса.
Слайд 37 1
2
Локоть Дюйм
3 4
Фут Фунт
2)Расположите единицы длины в порядке убывания.
№ 1, 3, 2
1 локоть ≈ 46 см 1 дюйм ≈ 2,5 см 1 фут ≈ 30 см
Слайд 39
1.Все ли представленные здесь преобразования являются движениями?
№ 4. Преобразование
подобия
Слайд 41Карлсон попросил у Малыша малинового варенья.
На полке стояли три банки
с вареньем. На первой было написано «Клубничное или малиновое», на
второй «Вишневое», а на третьей «Малиновое». В какой из них находится малиновое варенье, если известно, что фрекен Бок все надписи перепутала?Ответ: малиновое варенье находится во второй банке
Слайд 43
1
2 3
К.Ф.Гаусс Евклид Н.И.Лобачевский
1)Я думаю, что сначала жил Гаусс, затем Евклид и уже потом Лобачевский. Согласны ли вы с этим утверждением?
№ 1-2. Нет.
Слайд 44
1
2
3К.Ф.Гаусс Евклид Н.И.Лобачевский
2)Кому из этих учёных принадлежат слова: «Математика - царица наук, арифметика - царица математики»?
№ 1. К.Ф. Гаусс.
Слайд 45
1
2
3К.Ф.Гаусс Евклид Н.И.Лобачевский
3)Кто из них уже в 24-летнем возрасте был профессором университета?
№ 3. Н.И. Лобачевский.
Слайд 471. у = 3х2 – 2х5 + 1
2. у =
4 /(х2 + 3)
3. у = 7/ ( х –
5)4. у = х3 – 2
1. Верно ли, что областью определения всех данных функций является множество действительных чисел. Согласны ли вы с этим утверждением?
№ 3. D(у)={R\5}
Слайд 481. у = 3х2 – 2х5 + 1
2. у =
4 /(х2 + 3)
3. у = 7/ ( х –
5)4. у = х3 – 2
2. График какой функции не имеет общих точек с осью абсцисс?
№2.
Слайд 491. у = 3х2 – 2х5 + 1
2. у =
4 /(х2 + 3)
3. у = 7/ ( х –
5)4. у = х3 – 2
3. Графиком какой функции является гипербола?
№3.
Слайд 55
1
2
3 43. Какая из предложенных кривых является графиком ни четной, ни нечетной функции?
№ 3
Слайд 571. S = ½ ab sin γ
2.
S = ½ ah
3. S = abc /(4R)
4.
S = ½ (a + b) h Перед вами формулы площадей некоторых фигур. Я считаю, что всё это площади треугольника. Так ли это?
№ 4. Под номером 4 помещена формула для
вычисления площади трапеции.
Похожие презентации
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.