Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование графиков тригонометрических функций y=sin x и y=cosx
Содержание
- 1. Преобразование графиков тригонометрических функций y=sin x и y=cosx
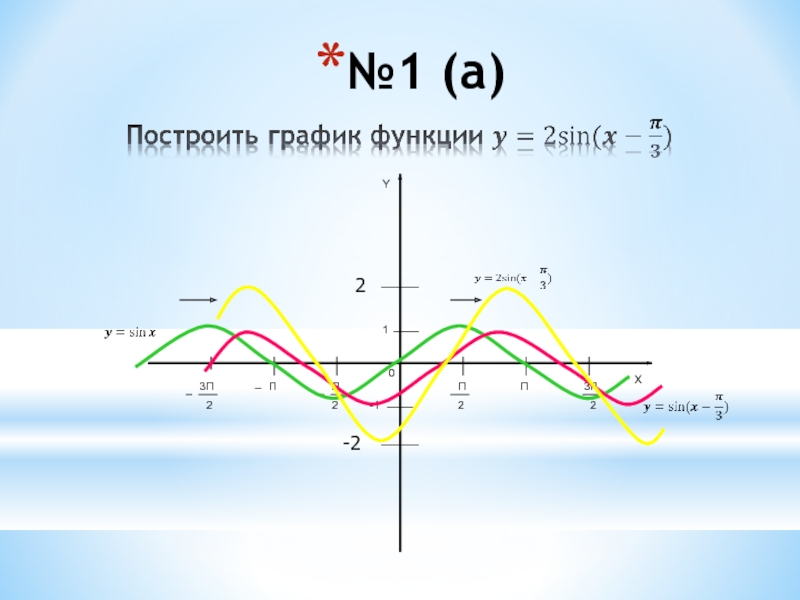
- 2. №1 (а)10-1ПП3П2П2П3П2YX 2-2
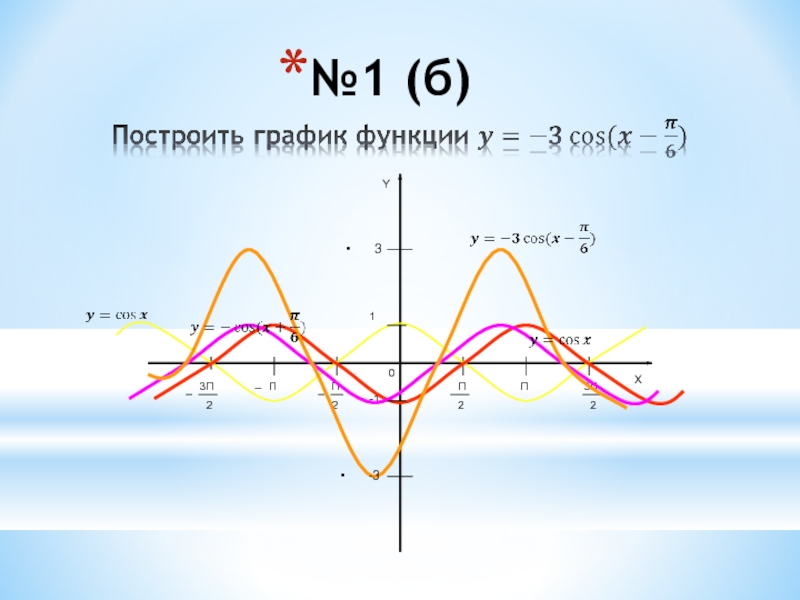
- 3. №1 (б)10-1ПП3П2П2П3П2YX -33
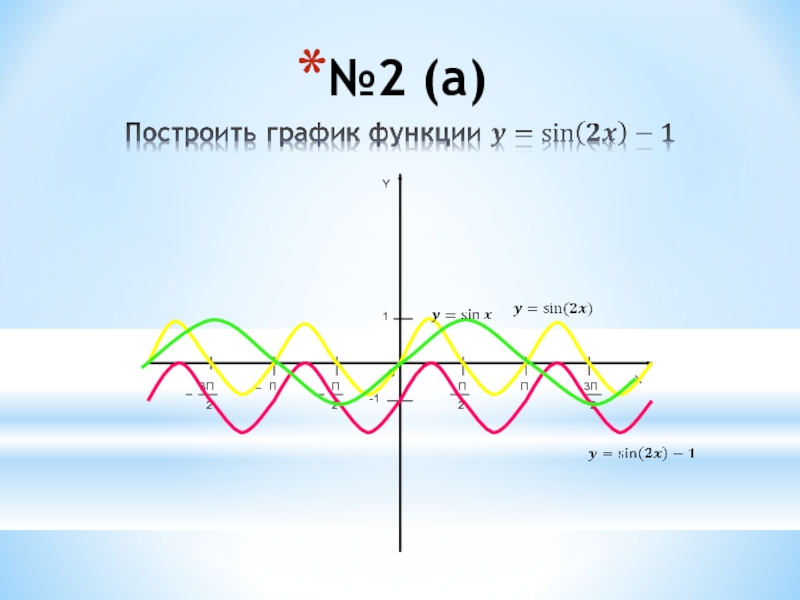
- 4. №2 (а)10-1ПП3П2П2П3П2YX
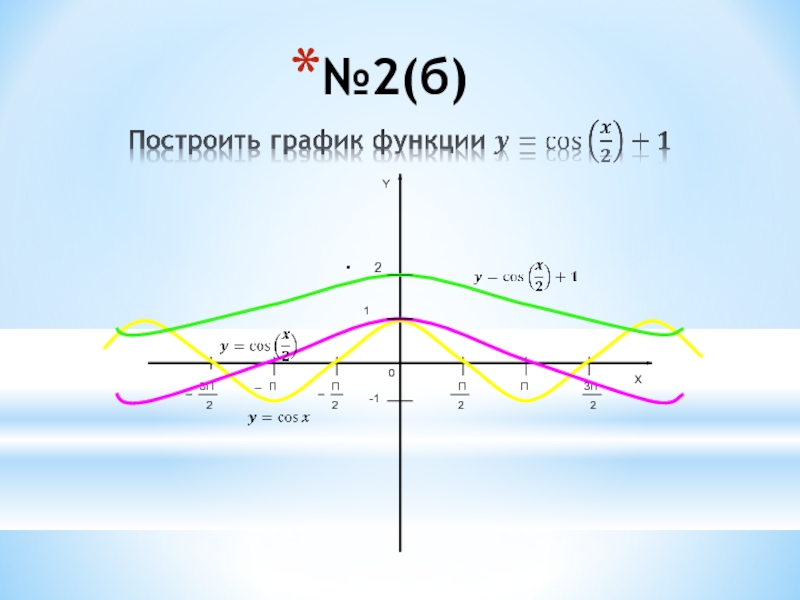
- 5. №2(б)10-1ПП3П2П2П3П2YX 2
- 6. Вспомним виды преобразований, которые используются для построения графиков функций.
- 7. Y=f (x)+af (x)Если a>0 f (x)
- 8. Y = f (x) + aaf (x)f (x) +aесли a
- 9. Y = f (x-a)af (x-a)f (x)если a>00График
- 10. Y = f (x-a)af (x-a)f (x)если a
- 11. Y = k f (x) k f
- 12. Y = k f (x)f (x)k f (x)0
- 13. Y = f (k x)f (k x)f
- 14. Y = f (k x)f (x)f (k x)0
- 15. Y = -f (x) f (x) -f
- 16. А) y= -2 sinxБ)y= cos x/2В)y= 1,5
- 17. А) y= -2 sinxБ)y= cos x/2В)y= 1,5
- 18. А) y= -2 sinxБ)y= cos x/2В)y= 1,5
- 19. А) y= -2 sinxБ)y= cos x/2В)y= 1,5
- 20. Ответы к заданиям.1 Г2 А3 Ж4 Е5 Д6 В7 Б8 З
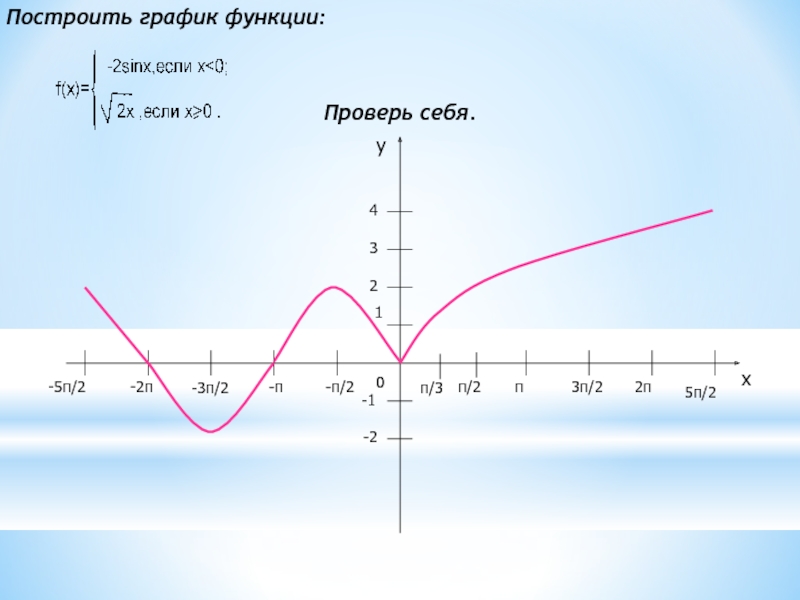
- 21. 0хy4321-1-2-п/2-п-3п/2-2п-5п/2п/2п3п/22п5п/2п/3 Построить график функции:Проверь себя.
- 22. Использование тригонометрических функций при описании и изучении
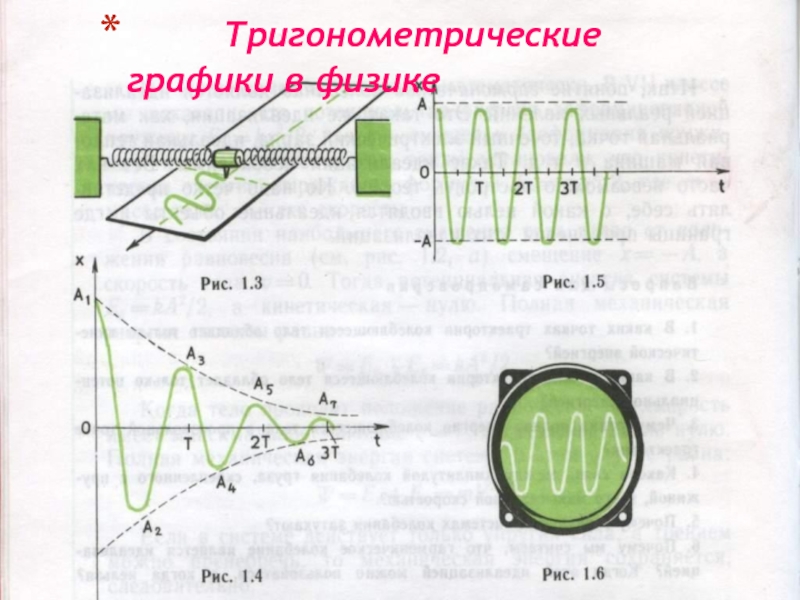
- 23. Тригонометрические графики в физике
- 24. Биение сердца
- 25. Восход Солнца
- 26. Заход Солнца
- 27. Фазы Луны
- 28. Морские приливы и отливы.
- 29. Затмение Солнца
- 30. Скачать презентанцию
№1 (а)10-1ПП3П2П2П3П2YX 2-2
Слайды и текст этой презентации
Слайд 1Преобразование графиков тригонометрических
функций y=sin x, y= cos x.
Учитель Фоминок
Светлана
Сергеевна
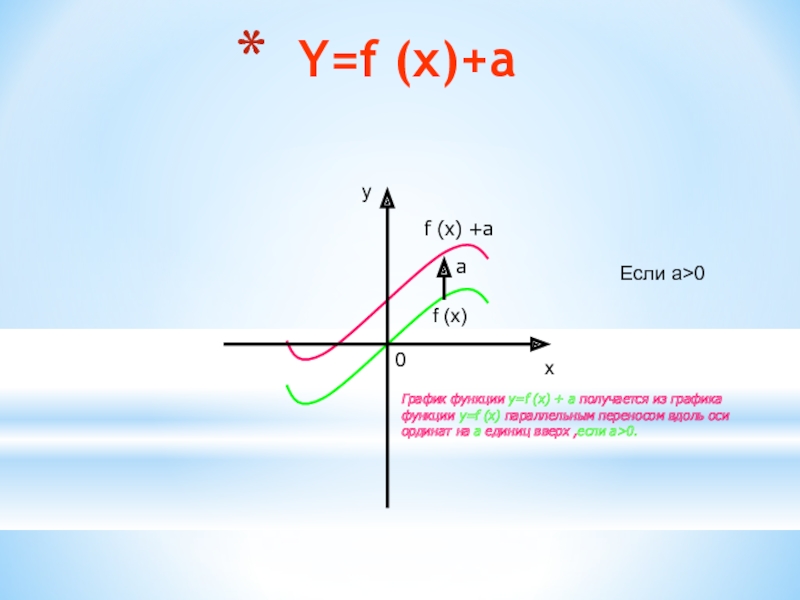
Слайд 7 Y=f (x)+a
f (x)
Если a>0
f (x) +a
0
a
График функции y=f
(x) + a получается из графика
функции y=f (x) параллельным переносом
вдоль осиординат на a единиц вверх ,если a>0.
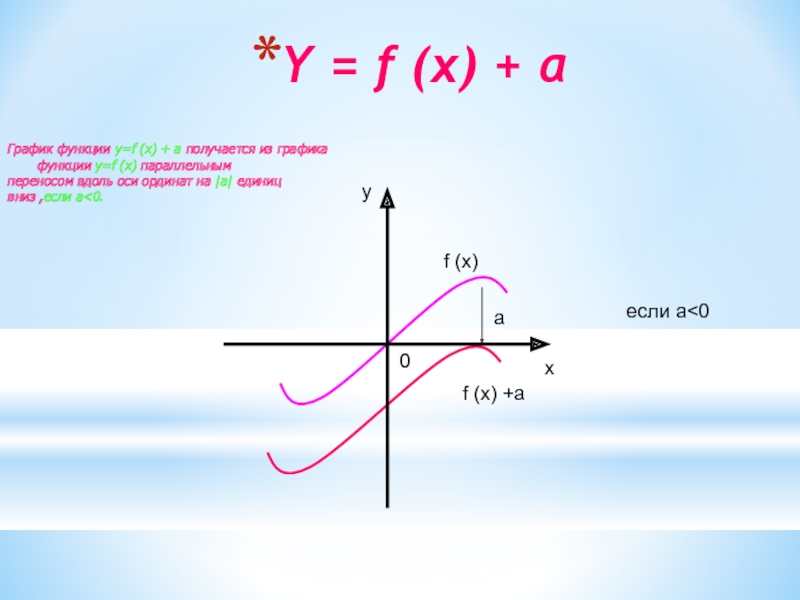
Слайд 8Y = f (x) + a
a
f (x)
f (x) +a
если a
функции y=f (x) + a получается из графика функции y=f
(x) параллельнымпереносом вдоль оси ординат на |a| единиц
вниз ,если a<0.
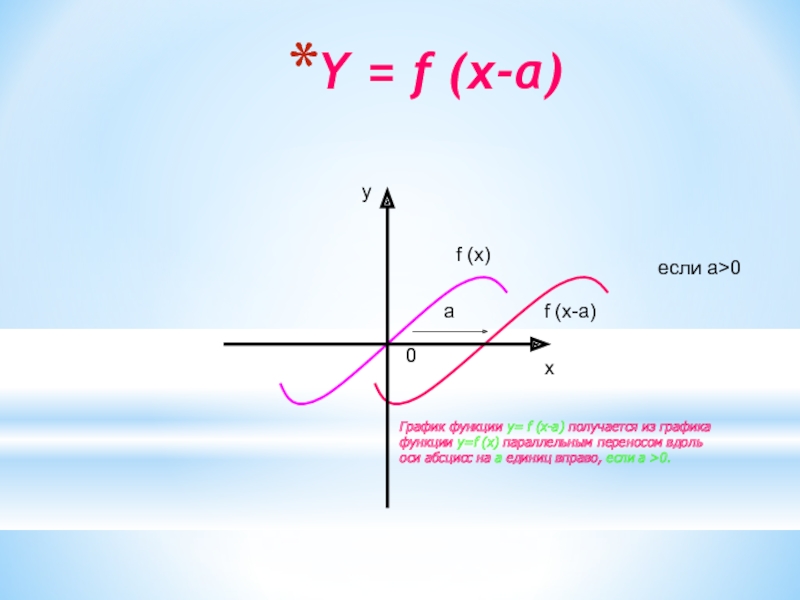
Слайд 9Y = f (x-a)
a
f (x-a)
f (x)
если a>0
0
График функции y= f
(x-a) получается из графика
функции y=f (x) параллельным переносом вдоль
оси абсцисс на а единиц вправо, если а >0.
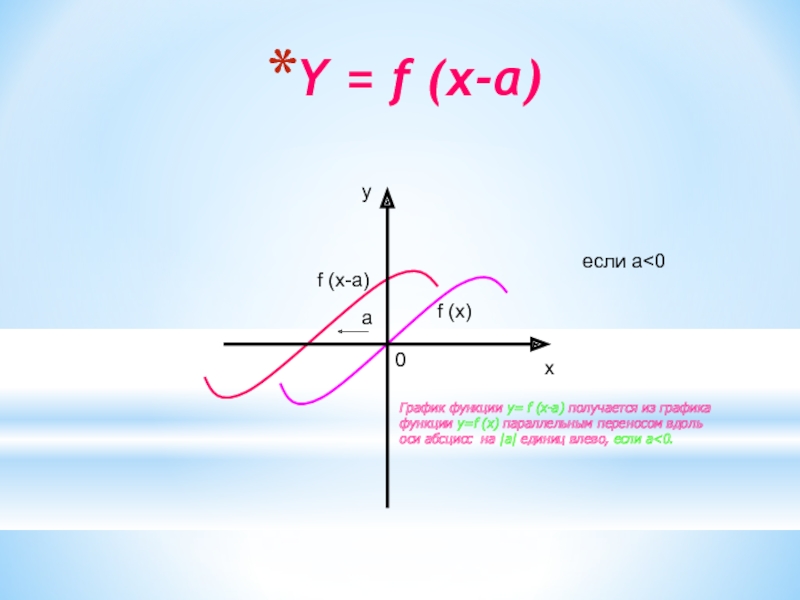
Слайд 10Y = f (x-a)
a
f (x-a)
f (x)
если a
(x-a) получается из графика
функции y=f (x) параллельным переносом вдоль
оси абсцисс на |а| единиц влево, если a<0.
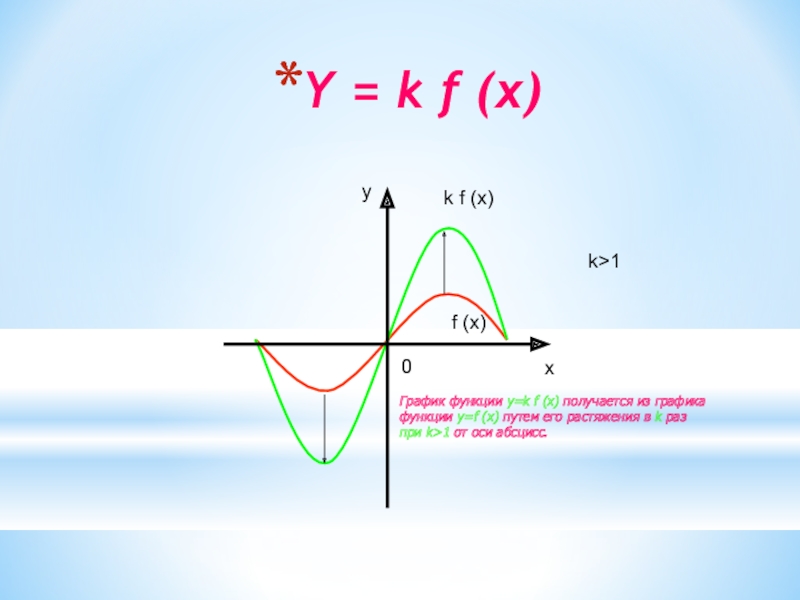
Слайд 11Y = k f (x)
k f (x)
k>1
f (x)
0
График функции
y=k f (x) получается из графика
функции y=f (x) путем его
растяжения в k разпри k>1 от оси абсцисс.
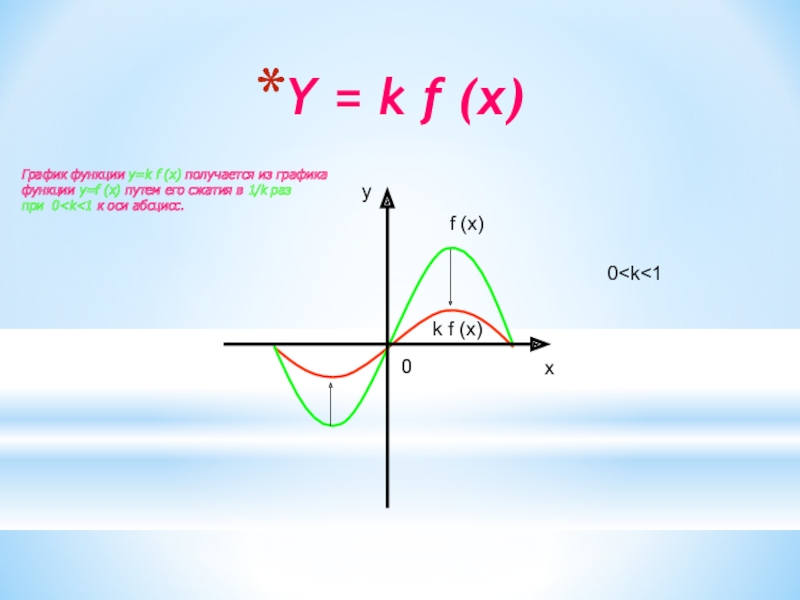
Слайд 12Y = k f (x)
f (x)
k f (x)
0
f (x) получается из графика
функции y=f (x) путем его сжатия
в 1/k разпри 0
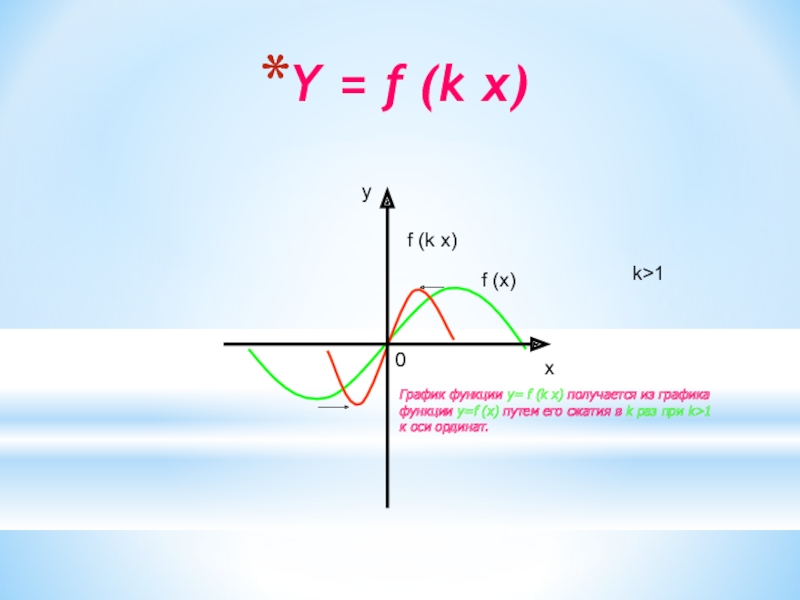
Слайд 13Y = f (k x)
f (k x)
f (x)
k>1
0
График функции y=
f (k x) получается из графика
функции y=f (x) путем его
сжатия в k раз при k>1к оси ординат.
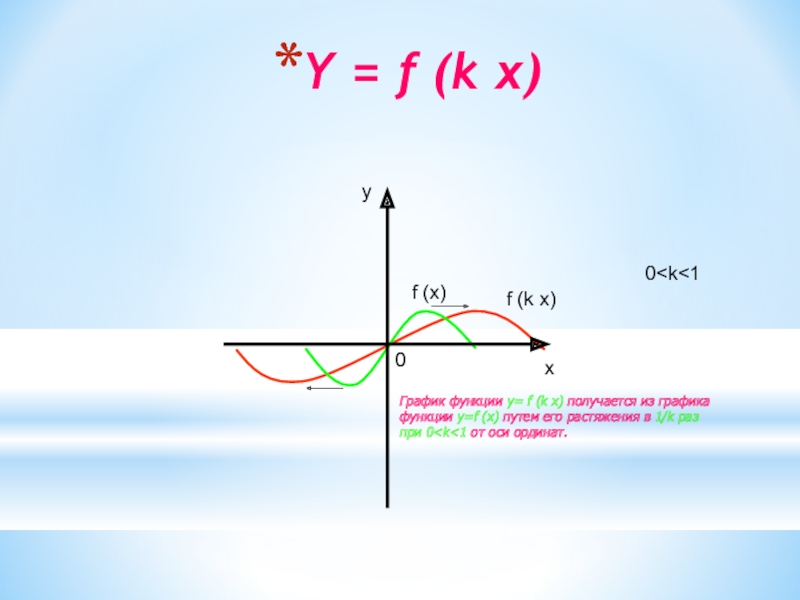
Слайд 14Y = f (k x)
f (x)
f (k x)
0
f (k x) получается из графика
функции y=f (x) путем его
растяжения в 1/k разпри 0
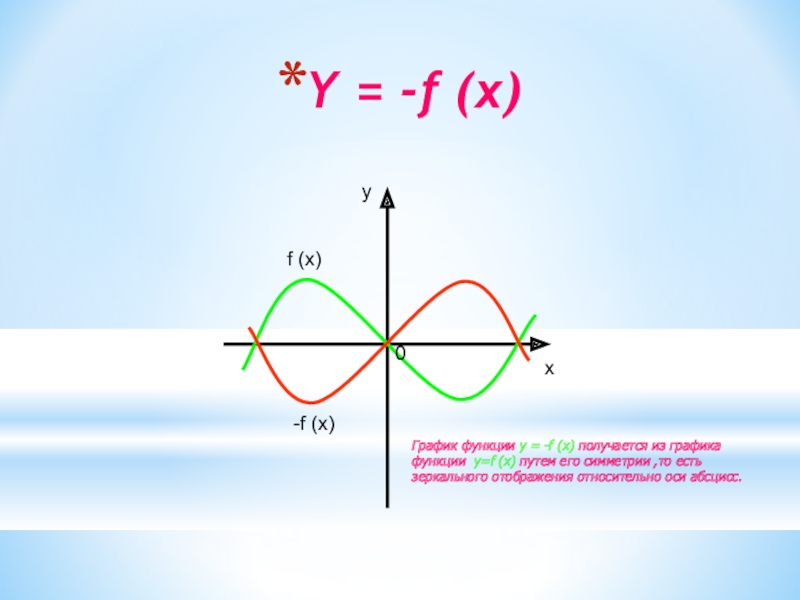
Слайд 15Y = -f (x)
f (x)
-f (x)
0
График функции y
= -f (x) получается из графика
функции y=f (x) путем
его симметрии ,то есть зеркального отображения относительно оси абсцисс.
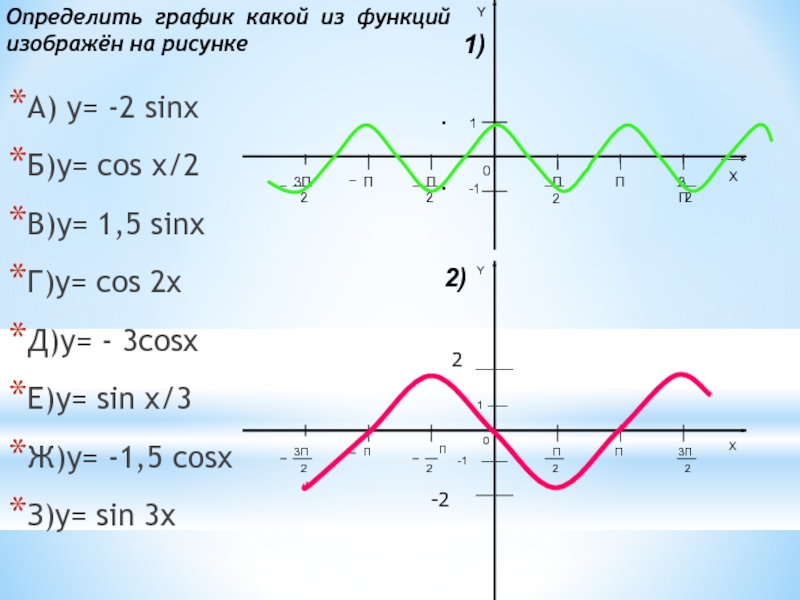
Слайд 16А) y= -2 sinx
Б)y= cos x/2
В)y= 1,5 sinx
Г)y= сos 2x
Д)y=
- 3cosx
Е)y= sin x/3
Ж)y= -1,5 cosx
З)y= sin 3x
0
П
П
3П
2
П
2
П
3П
2
Y
X
-1
1
1)
1
0
-1
П
П
3П
2
П
2
П
3П
2
Y
X
2)
2
-2
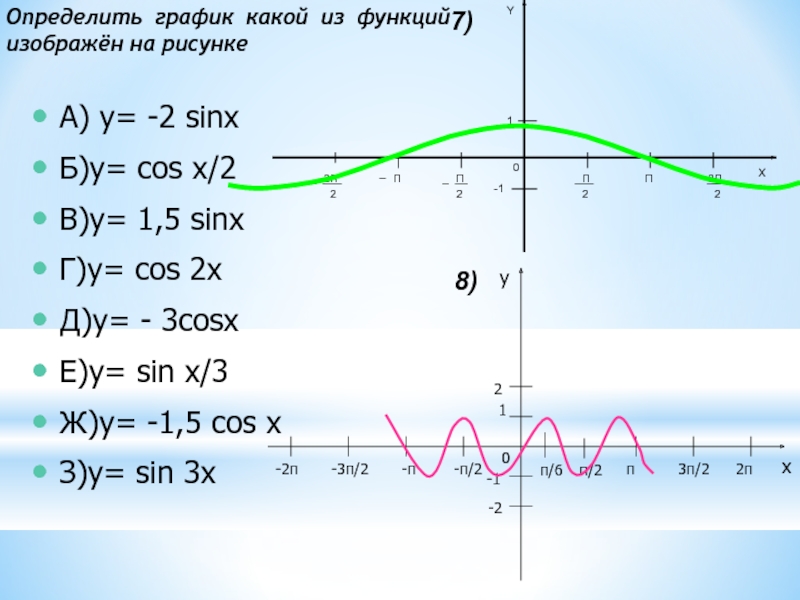
Определить график какой
из функций изображён на рисункеСлайд 17А) y= -2 sinx
Б)y= cos x/2
В)y= 1,5 sinx
Г)y= сos 2x
Д)y=
- 3cosx
Е)y= sin x/3
Ж)y= -1,5 cosx
З)y= sin 3x
X
1
0
-1
П
П
3П
2
П
2
П
3П
2
Y
3)
1
0
-1
П
П
3П
2
П
2
П
3П
2
Y
X
4)
-1.5
1.5
3п
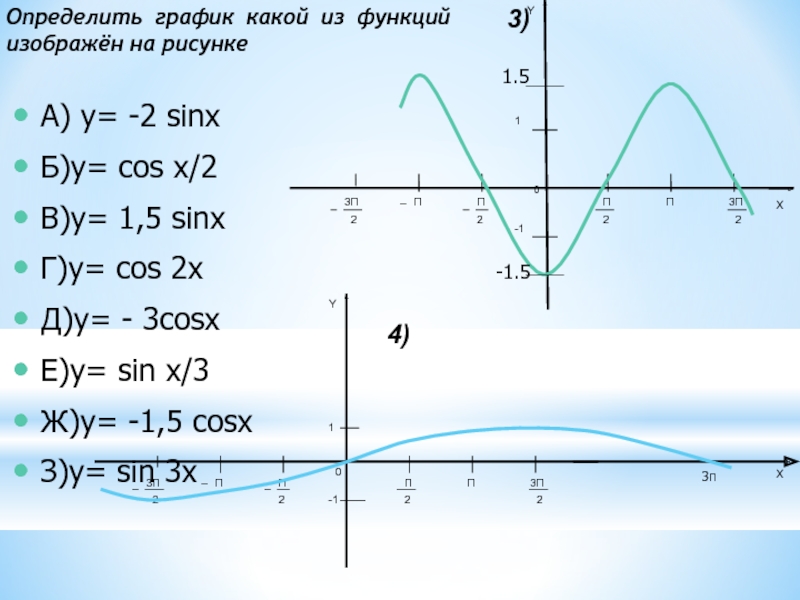
Определить график какой
из функций изображён на рисункеСлайд 18А) y= -2 sinx
Б)y= cos x/2
В)y= 1,5 sinx
Г)y= сos 2x
Д)y=
- 3cosx
Е)y= sin x/3
Ж)y= -1,5 cos x
З)y= sin 3x
1
0
-1
П
П
3П
2
П
2
П
3П
2
Y
X
3
-3
5)
1
0
-1
П
П
3П
2
П
2
П
3П
2
Y
X
6)
1,5
-1,5
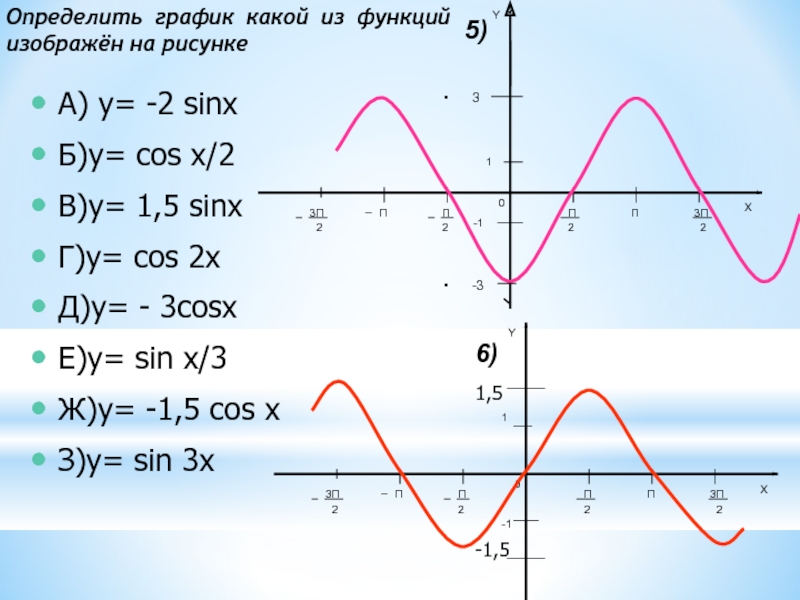
Определить график
какой из функций изображён на рисункеСлайд 19А) y= -2 sinx
Б)y= cos x/2
В)y= 1,5 sinx
Г)y= сos 2x
Д)y=
- 3cosx
Е)y= sin x/3
Ж)y= -1,5 cos x
З)y= sin 3x
7)
8)
0
х
y
2
1
-1
-2
-п/2
-п
-3п/2
-2п
п/2
п
3п/2
2п
п/6
Определить график
какой из функций изображён на рисункеСлайд 22Использование тригонометрических функций при описании и изучении различных жизненных процессов.
Восход
и заход Солнца, изменение фаз Луны, чередование времен года, затмение
и движение Планет, биение сердца, вращение колеса, морские приливы и отливы, эпидемии Гриппа.Все эти процессы периодичны, состояния участвующих в них объектов повторяются.