Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения квадратных и дробно-рациональных уравнений
Содержание
- 1. Методы решения квадратных и дробно-рациональных уравнений
- 2. Слайд 2
- 3. О математика. В веках овеяна
- 4. Слайд 4
- 5. Слайд 5
- 6. Квадратным уравнением называется уравнение
- 7. Слайд 7
- 8. СПОСОБЫ
- 9. Решение полных квадратных уравненийПо формуле корней квадратного уравнения: ax2+bx+c=0,
- 10. Дискриминант
- 11. Дискриминантпри квадратное уравнение имеет два корня
- 12. Дискриминантпри квадратное уравнение имеет один корень
- 13. Дискриминантпри квадратное уравнение не имеет корней
- 14. Формулы корней
- 15. Если хотя бы один из
- 16. 1.Если c=0 и b=0, то уравнение
- 17. Решение приведенного квадратного уравнения1.По формуле корней квадратного
- 18. Графический метод решения квадратных уравнений Чтобы получить
- 19. Графический метод решения квадратных уравненийФункция y1 это парабола.
- 20. Слайд 20
- 21. Решение биквадратного уравненияОпределение: уравнение вида ax4+bx2+c=0 называют
- 22. Решение квадратных уравнений Если все
- 23. Теорема Виета.Если x1
- 24. Решите?1.2.3.4.5.
- 25. Проверим…1. так как получили число меньше нуля, следовательно, уравнение корней не имеет
- 26. Проверим…2.
- 27. Проверим…3.
- 28. Проверим…4.найдем дискриминант так
- 29. Проверим…5.
- 30. Решение дробно рациональных уравненийПри решении уравнений, содержащих
- 31. Выдающаяся личность Виет
- 32. Слайд 32
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Содержание
Из истории
Определение
Классификация
Способы
решения
Теорема Виета
Проверка знаний
Решение дробно рациональных уравнений
Выдающаяся личность Виет
Слайд 3 О математика. В веках овеяна ты славой, Светило всех
земных светил. Тебя царицей величавой Недаром Гаусс окрестил. Строга, логична, величава, Стройна в полете,
как стрела, Твоя немеркнущая слава В веках бессмертье обрела. Мы славим разум человека, Дела его волшебных рук, Надежду нынешнего века, Царицу всех земных наук. Поведать мы сегодня вам хотим Историю возникновения Того, что каждый школьник должен знать – Историю квадратных уравнений.Слайд 4 Из истории
Необходимость решать уравнения не только первой, но и второй степени
еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:Слайд 5 Из
истории
Правило решения этих уравнений, изложенное
в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Слайд 6 Квадратным уравнением называется уравнение вида
где a, b, c, d – заданные числа, x
– переменная. Числа a, b, c носят следующие названия: a - первый коэффициент, b второй коэффициент, с - свободный член. ОПРЕДЕЛЕНИЕ
Слайд 7 КЛАССИФИКАЦИЯ
Полные: ax2+bx+c=0,
где коэффициенты b и с отличны от нуля;
Неполные: ax2+bx=0, ax2+c=0
или ax2=0т.е. хотя бы один из коэффициентов b или c равен нулю;
Приведенные: x2+bx+c=0,
т.е. уравнение, первый коэффициент которого равен единице (а=1).
Слайд 8 СПОСОБЫ РЕШЕНИЯ
Решение полных квадратных
уравнений
Дискриминант
Решение неполных квадратных уравнений
Решение приведенного квадратного уравнения
Графический метод решения квадратных
уравненийРешение биквадратных уравнений
Слайд 15 Если хотя бы один из коэффициентов c или
b равен нулю, то квадратное уравнение называется неполным квадратным
уравнением.Решение неполных квадратных уравнений
Слайд 16 1.Если c=0 и b=0, то уравнение ax2=0 имеет
один корень x=0;
2.Если c=0, то уравнение ax2+bx=0
имеет два корня:3.Если b=0, то уравнение ax2+c=0
при не имеет корней,
при имеет два корня
Слайд 17Решение приведенного квадратного уравнения
1.По формуле корней квадратного уравнения
2. Метод
выделения полного квадрата
Пример.
x2+2x-3=0 x2+2x=3,
x2+2x+1=3+1
(x+1)2=4
x+1=2 или x+1=-2
x1=1, x2=-3
3. По теореме обратной теореме Виета
x2+bx+c=0
х1+х2=-b,
x1×x2=c.
Слайд 18Графический метод решения квадратных уравнений
Чтобы получить решение квадратного уравнения
графическим способом Квадратное уравнение разделяют на две функции, линейную и
квадратичную. А затем строят графики этих функций на одной координатной плоскости.Квадратное уравнение
Разбивают на 2 части
ах^2+bx+c=0
y1 =ax^2
y2 =-(bx+c)
-
-
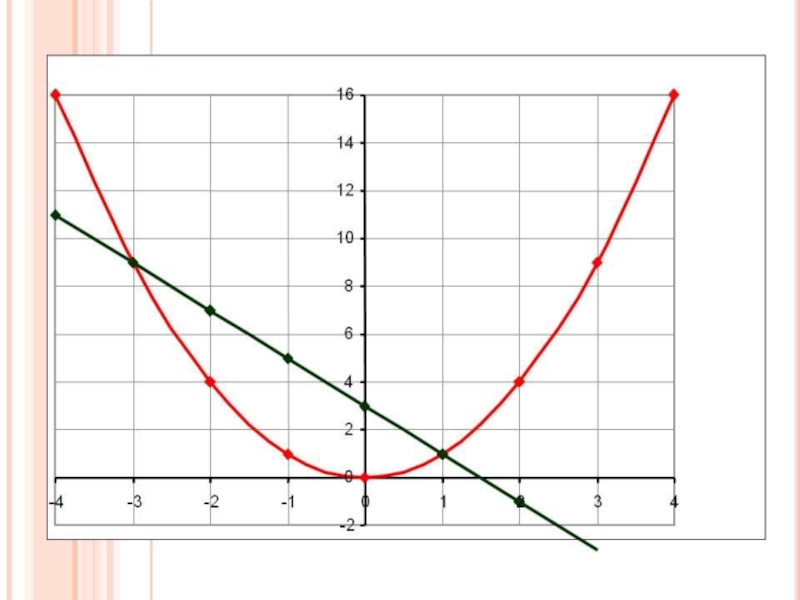
Слайд 19Графический метод решения квадратных уравнений
Функция y1 это парабола. Функция y2 это прямая
линия. Решением, корнями квадратного уравнения являются точки пересечения этих функций.
При
решении могут представиться три варианта:Функции имеют две точки пересечения - два корня квадратного уравнения действительны и различны между собой.
Функции имеют одну точку пересечения - квадратное уравнение имеет только один действительный корень.
Функции не имеют ни одной точки пересечения - тогда оба корня квадратного уравнения мнимые, комплексные числа.
Слайд 21Решение биквадратного уравнения
Определение: уравнение вида ax4+bx2+c=0 называют биквадратным.
Пример.
9x4+5x2-4=0
Обозначим x2=t. Тогда данное уравнение
примет вид9t2+5t-4=0
Откуда t1=9/4, t2=-1.
Уравнение x2=4/9 имеет корни x1=2/3, x2=-2/3 ,
а уравнение x2=-1 не имеет действительных корней.
Слайд 22Решение квадратных уравнений
Если все коэффициенты квадратного уравнения
отличны от нуля, то находим дискриминант.
Если квадратное
уравнение является приведенным, то можем его решить с помощью теоремы Виета.Слайд 23 Теорема Виета.
Если x1 и х2 –
корни приведенного квадратного уравнения х2+рх+q=0, то х1+х2= - р, х1
. х2=q.Если коэффициент при квадрате переменной равен 1, то уравнение называется приведенным.
Слайд 28Проверим…
4.
найдем дискриминант
так как дискриминант меньше
нуля, следовательно, квадратное уравнение не имеет корней
Слайд 30Решение дробно рациональных уравнений
При решении уравнений, содержащих переменную в знаменателе
дроби сначала нужно избавиться от дроби. Для этого находят наименьший
общий знаменатель, и обе части уравнения умножают на этот знаменатель. Далее полученное выражение упрощают, и получается обыкновенное линейное или квадратное уравнение.Только нужно найти область допустимых значений выражения (ОДЗ). После того, как найдены корни уравнения, обязательно проверяем, входят ли они в ОДЗ.
Вспомним два правила решения уравнений:
1) Если обе части уравнения разделить или умножить на одно и то же число, корни уравнения не изменятся.
2) Слагаемые можно переносить из одной части уравнения в другую с противоположным знаком.