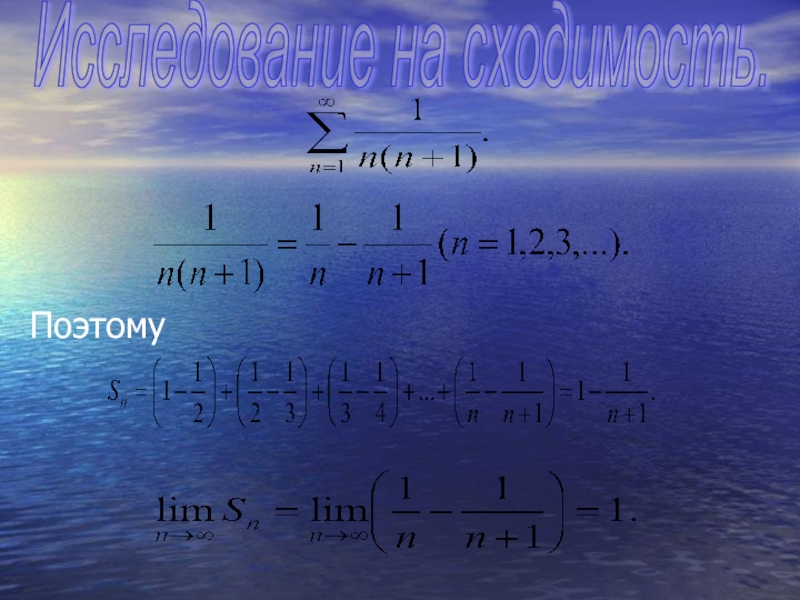Понятие числового ряда

2009 год

ряды
Признак Даламбера, исследование на сходимость
Использованная литература и программное обеспечение.
Содержание.

U1, u2, u3, un, …,
и с понятием бесконечных рядов

u1 + u2 + u3 + … + un + …
числа u1, u2 , u3, … - члены ряда.
Пользуясь введенным Эйлером знаком суммы ,
рассмотрим частичные суммы данного ряда.
s1 = u1 – первая частичная сумма,
s2 = u1 + u2 –вторая частичная сумма,
s3 = u1 + u2 + u3 – третья и т.д.
Сумма sn = u1 + u2 + u3 + … + un - частичная сумма ряда.

Определение числового ряда.

s1, s2 , s3, …,

sn, … , где

s1 = u1,
s2 = u1 + u2,
s3 = u1 + u2 + u3, ……………………………
sn = u 1+ u2 + u3 + … + un,
……………………………
При частичная сумма имеет предел

Сумма ряда.

частичных сумм
имеет конечный предел

Этот предел называется суммой сходящегося ряда.

Если последовательность частичных
сумм не имеет конечного предела, то ряд
называется расходящимся.

(-1) + … + (-1)n+1 + …
является рядом.
Составим

частичные суммы
s1 = 1, s2 = 1 - 1 = 0, s3 = 1 – 1 + 1 = 1, …,

Примеры числовых рядов.

рядом.
Из членов


составляют частичные суммы

Примеры числовых рядов.

+ … + n + … -
расходящийся, т.к.

последовательность его
частичных сумм
s1 = 1, s2 = 3, s3 = 6, … ,
имеет бесконечный предел.

Примеры сходящихся и расходящихся рядов.

+(-1)n+1 + … -
расходящийся, т.к. последовательность его
частичных сумм

не имеет никакого предела.

Примеры сходящихся и расходящихся рядов.

может сходится, когда общий член ряда un стремится к нулю:



Необходимое

условие сходимости ряда.

+ 0,4444 + … - расходится, т.к. общий член ряда

не стремиться к нулю.

Пример 6.
Ряд
1 – 1 + 1 – 1 + … - расходится, т.к. общий член
ряда не стремится к нулю.

Необходимое условие сходимости ряда.

сумм (Sn)
имеет предел:


который называют суммой бесконечно
убывающей геометрической прогрессии

(т.е.
суммой ряда).

что существует

,

то при ряд сходится,

а при ряд расходится.

признаком Даламбера:



ряд сходится.

академик Петербургской Академии наук, автор огромного количества научных открытий во

всех областях математики. Эйлер первым применил средства математического анализа в теории чисел, положил начало топологии.

Краткая историческая справка

имя по названию маленькой церкви на ступени которой он был

подброшен матерью. Жена бедного стекольщика заменила ему мать. Воспитатели Жана хотели, чтобы он был юристом или врачом, однако он стал математиком и срилососром.

Став знаменитостью и гордостью французской науки, Даламбер вознаградил стекольщика и его жену, следя за тем, чтобы они не оказались в нужде, и всегда с гордостью называл их своими родителями.

Жан Лерон Даламбер один из главных деятелей «Энциклопедии» и ее редакторов. С1751 г. вместе с Д. Дидро участвовал в её создании (1-й том вышел в 1/51—52 гг.). Написал введение к ней, являющееся одним из самых блестящих образцов «научного стиля». В срилососрии Даламбер был сторонником сенсуализма и противником декартовской теории врожденных идей.

не был последовательно материалистическим. По Даламберу, мышление не является свойством

материи, а душа имеет независимое от материи существование.

В противоположность другим французским просветителям он утверждал, что нравственность не обусловлена общественной средой. Даламбер признавал бога как образующую субстанцию. Критика непоследовательного сенсуализма Даламбера была дана в работах Дидро.

В "Трактате о динамике" (1758 г.) излагает свой принцип рассмотрения механической системы со связями, сводящий любую задачу динамики к задаче равновесия.

В 1794 г. избран во Французскую академию. В1757г. он покинул редакцию «Энциклопедии». В середине 1/60-х гг. Даламбер был приглашён российской императрицей Екатериной II в качестве воспитателя наследника престола, но он отказался принять приглашение.

математики» Москва, 1995;
А. Г. Цыпкин «Справочник по математике» Москва, 1983;
М.

Я. Выгодский «Справочник по высшей математике» Москва, 1997

Mathcad;
MS Power Point;
Windows Media;

MS Excel.